VORGESCHICHTE

Für einen Überblick zu allen vorausgehenden Beiträgen dieser rekonstruierenden Lektüre von Avicennas Beitrag zur Logik siehe AVICENNAS ABHANDLUNG ZUR LOGIK – BLITZÜBERSICHT.

BEGRIFFLICHKEIT NOCHMALS ÄNDERN

1. Für die Begriffe, die im Formalisierungsansatz eingeführt worden sind, der im vorausgehenden Blogeintrag Avicenna 14 vorgestellt wurde, legt es sich nach neuerlicher Überprüfung nahe, sie nochmals abzuändern.

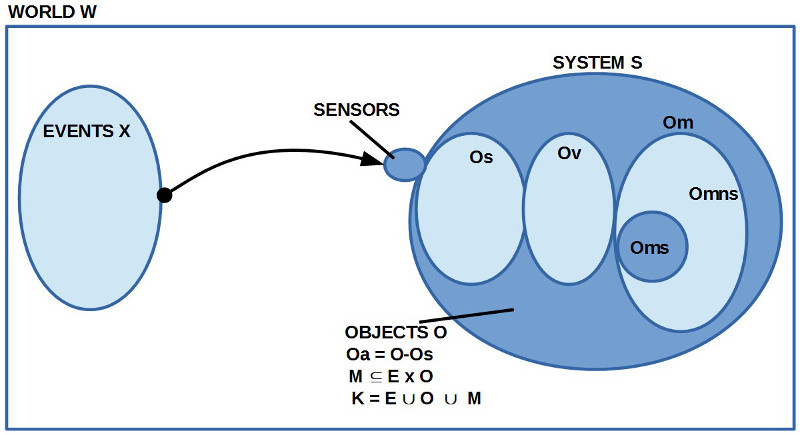
2. Die übergreifende Idee ist im obigen Diagramm angedeutet.

SYSTEM ALS TEIL EINER WELT

3. Die erste große Annahme besteht darin, dass das Wissen K, um das es in der Abhandlung zur Logik gehen soll, sich ‚in‘ einem System S befindet, das in einer umgebenden Welt W vorkommt.

WISSEN

4. Das Wissen K setzt sich zusammen aus den Komponenten $latex K = E \cup O \cup M$, d.h. das Wissen K umfasst die Komponenten ‚Ausdrücke‘ E, ‚Objekte‘ O sowie ‚Bedeutungsbeziehungen‘ M.

5. ‚Ausdrücke‘ E sind Verkettungen von Elementarelementen (‚Alphabet‘), die im Rahmen einer Sprache L zum Zweck der Kommunikation benutzt werden können.

6. ‚Objekte‘ O sind alle Bewusstseinsinhalte, die entweder aus der sinnlichen Wahrnehmungen Os stammen, aus der Erinnerung Om oder irgendwie vorgestellt/ gedacht sind Ov. Objekte O ohne die sinnlichen Objekte Os sollen hier auch ‚abstrakte‘ Objekte Oa genannt werden ($latex Oa = O – Os$). Im Bereich der erinnerten Objekte Om kann man auch noch unterscheiden zwischen solchen, die auf zuvor sinnliche Objekte Os zurückgehen Oms, oder solche, für die dies nicht zutrifft Omns, also ($latex Omns = Om – Oms$).

7. Die ‚Bedeutungsbeziehungen‘ M werden verstanden als eine Beziehung zwischen Ausdrücken E und Objeken O der Art $latex M \subseteq E \times O$. Spezieller könnte man auch definieren $latex Ms(E)=Os$, $latex Ma(E)=Oa$, usw.

NOTWENDIG – MÖGLICH

8. Die abstrakten Objekte Oa gelten als ’notwendig‘ $latex \boxempty$, wenn ihr ‚Erwartungswert‘ $latex \mu = 1$ ist, andernfalls gelten sie als ‚möglich‘ $latex \diamond$.

9. Der ‚Erwartungswert‘ $latex \mu$ ergibt sich aus der Häufigkeit des Auftretens von Objekten in der Erinnerung.

10. [Anmerkung: Diese Definition von ‚möglich‘ und ’notwendig‘ entspricht nicht ganz der ‚Intuition‘, dass etwas, was ’notwendig‘ ist, auf jeden Fall auch möglich sein sollte; allerdings folgt – intuitiv — aus der Möglichkeit keine Notwendigkeit. Die vorausgehende Definition von möglich und notwendig erinnert ein wenig an das ‚exklusive Oder‘, das auch ’schärfer‘ ist als das normale Oder. Nennen wie die hier benutzte Definition von ‚möglich‘ $latex \diamond$ und ’notwendig‘ $latex \boxempty$ daher auch die ‚exklusiven Modaloperatoren‘: Wenn etwas notwendig ist, dann ist es nicht möglich, und wenn etwas möglich ist, dann ist es nicht notwendig.]

11. [Anmerkung: wenn etwas ‚gedanklich notwendig‘ ist, folgt daraus in diesem Rahmen allerdings nicht, dass es auch tatsächlich sinnlich eintritt. Aus der gedanklichen Notwendigkeit folgt nur, dass es in der erinnerbaren Vergangenheit bislang immer eingetreten ist und daher die Erwartung sehr hoch ist, dass es wieder eintreten wird.]

ABSTRAKTIONSPROZESS – OBJEKTHIERARCHIE

12. Abstrakte Objekte Oa gehen aus den sinnlichen Objekten Os mittels eines Abstraktionsprozesses $latex \alpha$ hervor: $latex \alpha: Os \times Oa \longrightarrow Oa$.

13. Abstrakte Objekte Oa bilden eine ‚Objekthierarchie‘ derart, dass Objekte der Stufe j Objekte der Stufe $latex i < j$ als 'Instanzen' enthalten können. Sei das Objekt B eine Instanz von Objekt A, dann könnte man sagen 'B ist in A' oder 'A hat B'. ZUTREFFEN – ERFÜLLEN 14. Wenn es ein abstraktes Objekt a aus Oa gibt, das Instanzen $latex b_{1}, b_{2}, ...$ enthält, die mit aktuellen sinnlichen Objekten s aus Os 'hinreichen ähnlich' sind, dann soll gesagt werden, dass das abstrakte Objekt a auf s zutrifft bzw. dass das sinnliche Objekt s das abstrakte Objekt a 'erfüllt': $latex s \models a$. WAHR – FALSCH 15. Jetzt kann man auch sagen, wann Ausdrücke aus E 'wahr' oder 'falsch' sind. 16. Ein Ausdruck $latex A \in E$ soll genau dann als 'wahr' $latex (A)\top$ bezeichnet werden, wenn seine Bedeutung M(A) von einem sinnlichen Objekte $latex s \subseteq Os$ 'erfüllt' wird $latex s \models M(A)$. 17. Ein Ausdruck $latex A \in E$ soll genau dann als 'falsch' $latex (A)\bot$ bezeichnet werden, wenn seine Bedeutung M(A) nicht von einem sinnlichen Objekte $latex s \subseteq Os$ 'erfüllt' wird $latex s \not\models M(A)$. AUSSAGE-OPERATOREN 18. Jetzt kann man folgende Operatoren über Aussagen definieren: 19. NEGATION: die Verneinung einer Aussage A ist wahr, wenn die Aussage selbst falsch ist, also $latex (\neg A)\top \leftrightarrow (A)\bot$. 20. KONJUNKTION: die Konjunktion $latex \wedge$ von zwei Aussagen A und B ist wahr, wenn beide Aussagen zugleich wahr sind; ansonsten ist die Konjunktion falsch, also $latex (A \wedge B)\top \leftrightarrow (A)\top\ und\ zugleich\ (B)\top$; ansonsten falsch. 21. DISJUNKTION: die Disjunktion $latex \vee$ von zwei Aussagen A und B ist wahr, wenn eine von beiden Aussagen wahr ist; ansonsten ist die Disjunktion falsch, also $latex (A \vee B)\top \leftrightarrow (A)\top\ oder\ (B)\top$; ansonsten falsch. 22. EXKLUSIVE DISJUNKTION: die exklusive Disjunktion $latex \sqcup$ von zwei Aussagen A und B ist wahr, wenn genau eine von beiden Aussagen wahr ist; ansonsten ist die exklusive Disjunktion falsch, also $latex (A \sqcup B)\top \leftrightarrow\ Entweder\ (A)\top\ oder\ (B)\top$; ansonsten falsch. 23. IMPLIKATION: die Implikation $latex \rightarrow$ von zwei Aussagen A und B ist wahr, wenn nicht zugleich A wahr ist und B falsch, also $latex (A \rightarrow B)\top \leftrightarrow\ nicht zugleich (A)\top\ und\ (B)\bot$; ansonsten falsch. Fortsetzung folgt QUELLEN

• Avicenna, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
• Digital Averroes Research Environment
• Nicholas Rescher (1928 – ),The Development of Arabic Logic. University of Pittsburgh Press, 1964
• Stanford Encyclopedia of Philosophy, Aristotle’s Logic
• Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
• Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
• Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
• Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7

Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER.