(Letzte Änderung: 9.Juni 2023, 17:55h)

KONTEXT

Die aktuelle Phase meines Denkens kreist weiterhin um die Frage, wie sich die verschiedenen Erkenntniszustände zueinander verhalten: die vielen einzel-wissenschaftlichen Disziplinen treiben nebeneinander her; Philosophie beansprucht weiterhin eine Oberhoheit, kann sich aber selbst nicht wirklich überzeugend verorten; und das Denken im Alltag zieht weiterhin unbeirrt seine Bahnen mit der Überzeugung ‚Alles sei doch klar‘, man müsse doch nur einfach hinschauen ‚wie es ist‘. Dann kommen noch die verschiedenen ‚religiösen Anschauungen‘ um die Ecke mit einem sehr hohen Anspruch bei gleichzeitigem Verbot, nicht zu genau hinschauen zu dürfen. … und vieles mehr.

ABSICHT

Im folgenden Text werden drei fundamentale Betrachtungsweise unserer gegenwärtigen Welt skizziert und sie werden zugleich zueinander in Beziehung gesetzt. Manche bislang unbeantwortete Fragen lassen sich dadurch möglicherweise besser beantworten, viele neue Fragen entstehen aber auch. Wenn ‚alte Denkmuster‘ außer Kraft gesetzt werden, muss man viele (die meisten? Alle?) der bislang vertrauten Denkmuster neu justieren. Mit einem Mal sind sie schlicht ‚falsch‘ oder stark ‚reparaturbedürftig‘.

Leider ist es nur eine ‚Skizze‘.

DENKEN im ALLTAG

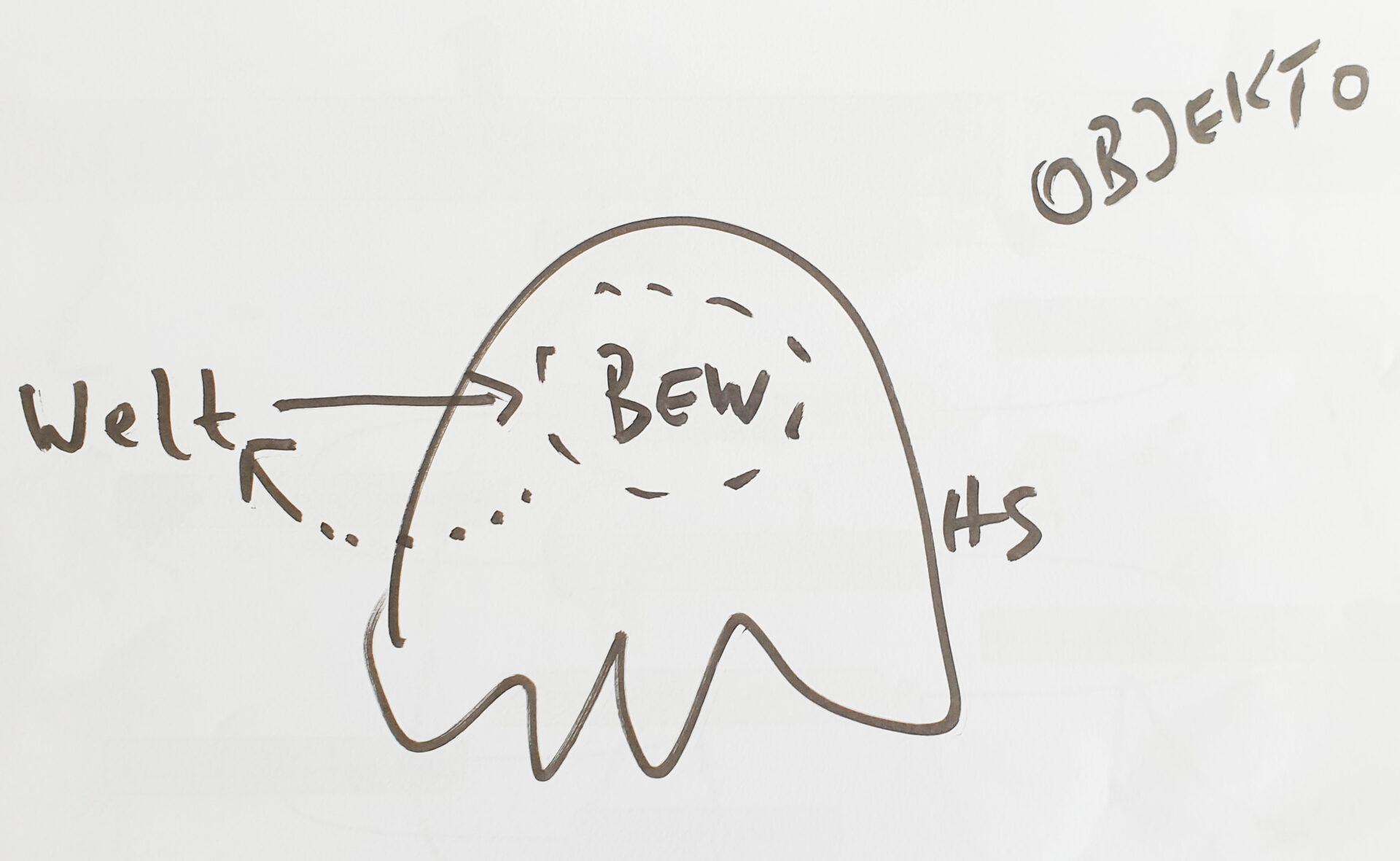
BILD 1: Im Alltagsdenken geht jeder Mensch (ein ‚homo sapiens‘ (HS)) davon aus, dass das, was er von einer ‚realen Welt‘ weiß, das ist, was er ‚wahrnimmt‘. Dass es diese reale Welt mit ihren Eigenschaften gibt, ist ihm — mehr oder weniger — ‚bewusst‘, darüber muss man nicht eigens diskutieren. Das, was ‚ist, ist‘.

… vieles wäre zu sagen …

PHILOSOPHISCHES DENKEN

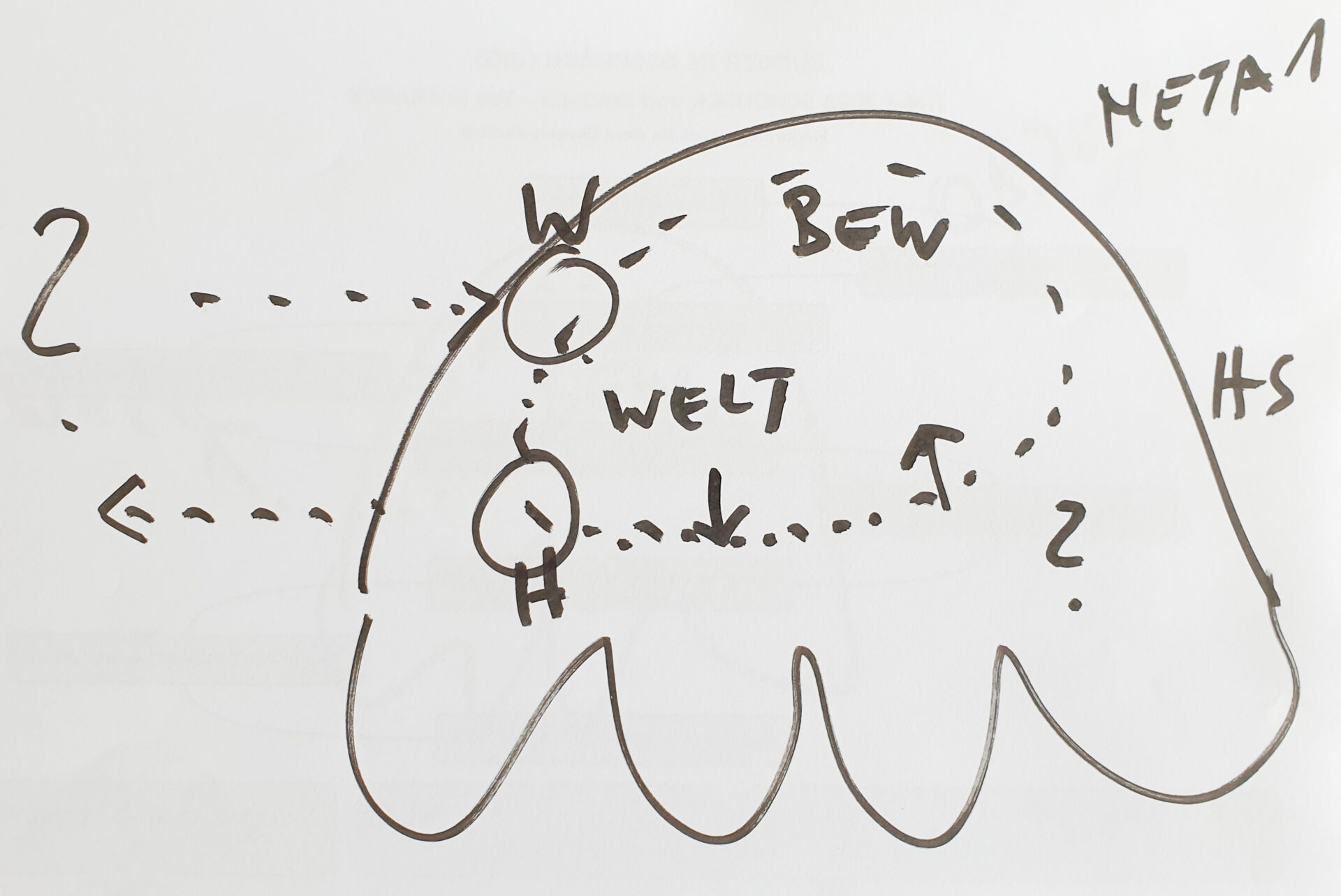
BILD 2: Das philosophische Denken beginnt dort, wo einem auffällt, dass die ‚reale Welt‘ nicht von allen Menschen in ‚gleicher Weise‘ wahrgenommen und noch weniger in gleicher Weise ‚vorgestellt‘ wird. Manche Menschen haben ‚ihre Vorstellungen‘ von der realen Welt, die markant ‚anders sind‘ als die Vorstellungen anderer Menschen, und doch bestehen sie darauf, dass die Welt genau so ist, wie sie sich das vorstellen. Aus dieser Beobachtung im Alltag, können viele neue Fragen entstehen. Die Antworten auf diese Fragen sind so vielfältig wie es Menschen gab und gibt, die sich diesen philosophischen Fragen hingaben oder noch hingeben.

… berühmte Beispiele: Platons Höhlengleichnis deutet an, dass die Inhalte unseres Bewusstseins vielleicht doch nicht ‚die Sachen selbst‘ sind sondern nur die ‚Schatten‘ vom dem, was letztlich ‚wahr‘ ist … Descartes berühmtes ‚cogito ergo sum‘ bringt den Aspekt ins Spiel, dass die Inhalte des Bewusstsein auch etwas über ihn selbst sagen, der solche Inhalte ‚bewusst wahrnimmt’…. die ‚Existenz der Inhalte‘ setzt seine ‚Existenz des Denkenden‘ voraus, ohne die die Existenz der Inhalte gar nicht möglich wäre …was sagt uns dies? … Kants berühmtes ‚Ding an sich‘ kann man auf die Einsicht beziehen, dass die konkreten, flüchtigen Wahrnehmungen niemals die ‚Welt als solche‘ in ihrer ‚Allgemeinheit direkt zeigen können. Diese liegt ‚irgendwo dahinter‘, schwer greifbar, eigentlich gar nicht greifbar? ….

… vieles wäre zu sagen …

EMPIRISCH-THEORETISCHES DENKEN

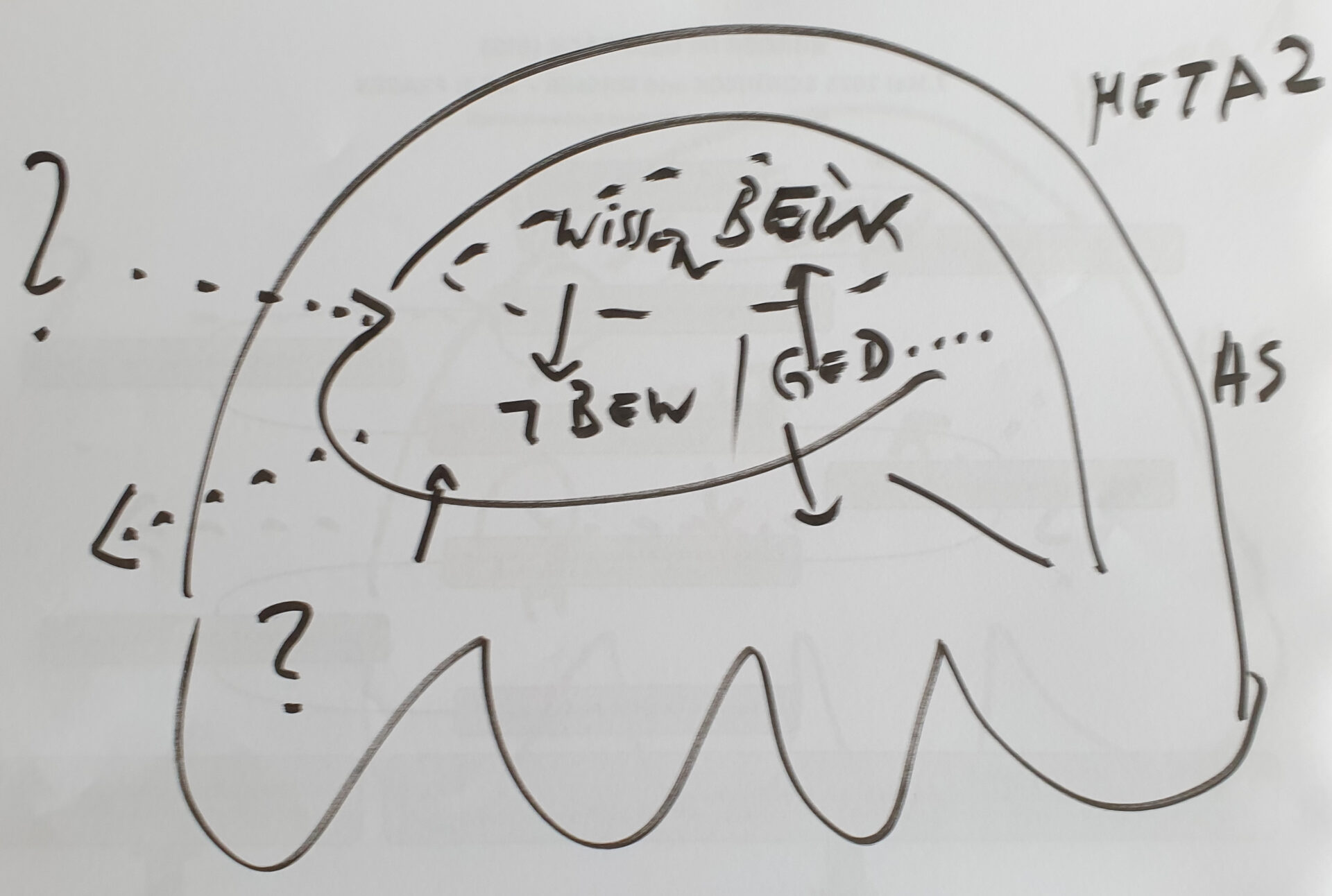
BILD 3: Das Konzept einer ‚empirischen Theorie‘ entwickelte sich sehr spät in der dokumentierten Geschichte des Menschen auf diesem Planeten. Einerseits philosophisch angeregt, andererseits unabhängig von den verbreiteten Formen von Philosophie, aber sehr stark beeinflusst von logischem und mathematischem Denken, siedelte sich das neue ‚empirische theoretische‘ Denken genau an dieser Bruchstelle zwischen ‚Alltagsdenken‘ und ‚theologischem‘ sowie ’stark metaphysischem philosophischem Denken‘ an. Dass Menschen ‚mit dem Brustton der Überzeugung‘ Aussagen über die Welt machen konnten, obwohl es nicht möglich war, ‚gemeinsame Erfahrungen der realen Welt‘ aufzuzeigen, die mit den geäußerten Aussagen ‚übereinstimmten‘, führte dazu, dass einzelne Menschen damit begannen, die ‚erfahrbare (empirische) Welt‘ so zu untersuchen, dass jeder andere bei ‚gleichem Vorgehen‘, die ‚gleichen Erfahrungen‘ machen konnte. Diese ‚transparenten Vorgehensweisen‘ waren ‚wiederholbar‘ und solche Vorgehensweisen wurden zu dem, was später als ‚empirisches Experiment‘ bzw. dann, noch einen Schritt weiter, als ‚Messen‘ bezeichnet wurde. Beim ‚Messen‘ vergleicht man das ‚Ergebnis‘ eines bestimmten experimentellen Vorgehens mit einem ‚zuvor definierten Standard-Objekt‘ (‚Kilogramm‘, ‚Meter‘, …).

Diese Vorgehensweise führte dazu, dass — zumindest die Experimentatoren — ‚lernten‘, dass unser Wissen um die ‚reale Welt‘ in zwei Komponenten zerfällt: es gibt das ‚allgemeine Wissen‘ was unsere Sprache artikulieren kann, mit Begriffen, die nicht automatisch etwas mit der ‚erfahrbaren Welt‘ zu tun haben müssen, und solchen Begriffen, die sich mit experimentellen Erfahrungen in Verbindung bringen lassen, und zwar so, dass auch andere Menschen, sofern sie sich auf das experimentelle Vorgehen einlassen, diese Erfahrungen wiederholen und dadurch bestätigen können. Eine grobe Unterscheidung zwischen diesen beiden Arten von sprachlichen Äußerungen könnte sein: ‚fiktive‘ Ausdrücke mit ungeklärtem Erfahrungsanspruch, und ‚empirische‘ Ausdrücke mit bestätigtem Erfahrungsanspruch.

Seit dem Beginn der neuen empirisch-theoretischen Denkweise im ca. 17.Jahrhundert dauerte es gut mindestens 300 Jahre, bis sich das Konzept einer ‚empirischen Theorie‘ soweit gefestigt hatte, dass es in weiten Bereichen der Wissenschaft zu einem prägenden Paradigma geworden war. Viele methodische Fragen blieben aber strittig oder blieben sogar ‚ungelöst‘.

DATEN und THEORIE

Viele Jahrhunderte wurde bei vielen — bei nicht wenigen auch bis in unsere Gegenwart — der ‚Missbrauch der Alltagssprache‘ für die Ermöglichung von ‚empirisch nicht verifizierbare Aussagen‘ direkt dieser Alltagssprache angekreidet und die gesamte Alltagssprache wurde als ‚Quelle von Unwahrheiten‘ diskreditiert. Eine Befreiung von diesem ‚ Monster Alltagssprache‘ wurde immer mehr in formalen Kunstsprachen gesucht bzw. dann in der modernen axiomatisierte Mathematik, die ein enges Bündnis mit der modernen formalen Logik eingegangen war (ab Ende des 19.Jahrhunderts). Die Ausdruckssysteme der modernen formalen Logik bzw. dann der modernen formalen Mathematik hatten als solche (nahezu) keine ‚Eigenbedeutung‘. Diese mussten fallweise explizit eingeführt werden. Eine ‚formale mathematische Theorie‘ konnte so formuliert werden, dass sie auch ohne ‚explizite Zuweisung‘ einer ‚externen Bedeutung‘ ‚logische Schlüsse‘ zulässt, die es erlaubten, bestimmte formale Ausdrücke als ‚formal wahr‘ oder ‚formal falsch‘ zu bezeichnen.

Dies erschien auf den ersten Blick sehr ‚beruhigend‘: die Mathematik als solche ist kein Ort von ‚falschen‘ oder ‚untergejubelten‘ Wahrheiten.

Der intensive Einsatz formaler Theorien in Verbindung mit erfahrungsbasierten Experimenten machte aber dann schrittweise deutlich, dass ein einzelner Messwert als solcher eigentlich auch keine ‚Bedeutung‘ besitzt: was soll es ‚bedeuten‘ dass man zu einem bestimmten ‚Zeitpunkt‘ an einem bestimmten ‚Ort‘ einen ‚erfahrbaren Zustand‘ mit bestimmten ‚Eigenschaften‘ feststellt, im Idealfall einem zuvor vereinbarten ‚Standardobjekt‘ vergleichbar? ‚Ausdehnungen‘ von Körpern können sich ändern, ‚Gewicht‘ und ‚Temperatur‘ ebenso. Alles kann sich in der Erfahrungswelt ändern, schnell, langsam, … was kann also ein einzelner isolierter Messwert sagen?

So manchem dämmerte es — nicht nur den erfahrungsbasierten Forschern, sondern auch verschiedenen Philosophen –, dass einzelne Messwerte nur eine ‚Bedeutung‘, einen möglichen ‚Sinn‘ bekommen, wenn man mindestens ‚Beziehungen‘ zwischen einzelnen Messwerten herstellen kann: Beziehungen ‚in der Zeit‘ (vorher – nachher), Beziehungen am/im Ort (höher – tiefer, nebeneinander, …), ‚zusammenhängende Größen‘ (Objekte – Flächen, …), und dass darüber hinaus die verschiedenen ‚Beziehungen‘ selbst nochmals einen ‚begrifflichen Kontext‘ benötigen (einzeln – Menge, Wechselwirkungen, kausal – nicht kausal, …).

Schließlich wurde damit auch klar, dass einzelne Messwerte darüberhinaus ‚Klassenbegriffe‘ benötigten, damit man sie überhaupt irgendwie einordnen konnte: abstrakte Begriffe wie ‚Baum‘, ‚Pflanze‘, ‚Wolke‘, ‚Fluss‘, ‚Fisch‘ usw. wurden so zu ‚Sammelstellen‘, bei denen man ‚Einzelbeobachtungen‘ abliefern konnte. Damit konnten dann aberhundert Einzelwerte z.B. zur Charakterisierung des abstrakten Begriffs ‚Baum‘ oder ‚Pflanze‘ usw. benutzt werden.

Diese Unterscheidung in ‚einzeln, konkret‘ und ‚abstrakt, allgemein‘ erweist sich als fundamental. Sie machte auch deutlich, dass die Einteilung der Welt mit Hilfe von solchen abstrakten Begriffen letztlich ‚willkürlich‘ ist: sowohl ‚welche Begriffe‘ man wählt ist willkürlich, als auch die Zuordnung von einzelnen Erfahrungsdaten zu abstrakten Begriffen ist nicht vorab eindeutig geregelt. Der Prozess der Zuordnung von einzelnen Erfahrungsdaten zu bestimmten Begriffen innerhalb eines ‚Prozesses in der Zeit‘ ist selbst stark ‚hypothetisch‘ und selbst wiederum Teil von anderen ‚Beziehungen‘ die zusätzliche ‚Kriterien‘ liefern können, ob nun Datum X eher zum Begriff A oder eher zum Begriff B gehört (die Biologie ist voll von solchen Klassifikationsproblemen).

Ferner zeigte sich, dass die so ‚unschuldig‘ daher kommende Mathematik bei näherer Betrachtung keineswegs als ‚unschuldig‘ gelten kann. Die breite Diskussion der Wissenschaftsphilosophie im 20.Jahrhundert brachte viele ‚Artefakte‘ zur Sprache, welche die Beschreibung einer dynamischen Erfahrungswelt mindestens leicht ‚korrumpieren‘ kann.

So gehört es zu formalen mathematischen Theorien, dass sie mit sogenannten ‚All- oder Partikularaussagen‘ operieren können. Mathematisch ist es wichtig, dass ich über ‚alle‘ Elemente eines Bereichs/ einer Menge reden kann. Ansonsten wird das Reden sinnlos. Wenn ich nun ein formales mathematisches System als begrifflichen Rahmen für eine Theorie wähle, die ‚empirische Sachverhalte‘ so beschreibt, dass Folgerung möglich werden, die im Sinne der Theorie ‚wahr sind‘ und damit zu ‚Prognosen‘ werden, die behaupten, dass ein bestimmter Sachverhalt entweder ‚absolut‘ oder mit einer bestimmten Wahrscheinlichkeit X größer 50% eintreten wird, dann vereinigen sich zwei verschiedene Welten: die fragmentarischen Einzelaussagen über die Erfahrungswelt werden eingebettet in ‚Allaussagen‘, die grundsätzlich mehr sagen, als Erfahrungsdaten bereit stellen können.

An dieser Stelle wird sichtbar, dass die so ’neutral‘ erscheinende Mathematik genau den gleichen Job tut wie die ‚Alltagssprache‘ mit ihren ‚abstrakten Begriffen‘: die abstrakten Begriffe der Alltagssprache gehen immer über den Einzelfall hinaus (sonst könnten wir letztlich gar nichts sagen), aber gerade dadurch erlauben sie Überlegungen und Planungen, wie wir sie an den mathematischen Theorien so schätzen.

Empirische Theorien im Format formaler mathematischer Theorien haben das weitere Problem, dass sie ja als solche über (nahezu) keine eigene Bedeutungen verfügen. Will man die formalen Ausdrücke mit der Erfahrungswelt in Beziehung setzen, dann muss man (mit Hilfe der Alltagssprache!) für jeden abstrakten Begriff der formalen Theorie (oder auch für jede formale Beziehung oder auch für jeden formalen Operator) explizit eine ‚Bedeutung konstruieren‘, indem man zwischen den abstrakten Konstrukten und bestimmten aufweisbaren Erfahrungstatsachen eine ‚Abbildung’/ eine ‚Zuordnung‘ herstellt. Was sich hier auf den ersten Blick vielleicht so einfach anhört, hat sich im Laufe der letzten 100 Jahren als ein fast unlösbares Problem erwiesen. Daraus folgt jetzt nicht, dass man es überhaupt nicht tun sollte; es macht aber darauf aufmerksam, dass die Wahl einer formalen mathematischen Theorie nicht automatisch eine gute Lösung sein muss.

… vieles wäre noch zu sagen …

FOLGERN und WAHRHEIT

Eine formale mathematische Theorie kann aus bestimmten ‚Annahmen‘ bestimmte Aussagen als formal ‚wahr‘ oder ‚falsch‘ ableiten. Dies geht, weil es zwei grundlegende Voraussetzungen gibt: (i) Alle formalen Ausdrücke haben einen ‚abstrakten Wahrheitswert‘ als ‚abstrakt wahr‘ oder eben als ‚abstrakt nicht wahr‘. Ferner gibt es einen sogenannten ‚formalen Folgerungsbegriff‘, der festlegt, ob und wie man aus einer gegebenen ‚Menge von formalen Ausdrücken‘ mit vereinbarten abstrakten Wahrheitswerten und einer klar definierten ‚Form‘ andere formalen Ausdrücke ‚ableiten‘ kann. Dieses ‚Ableiten‘ besteht aus ‚Operationen über den Zeichen der formalen Ausdrücke‘. Die formalen Ausdrücke sind hier ‚Objekte‘ des Folgerungsbegriffs, der auf einer ‚Ebene höher‘ angesiedelt ist, auf einer ‚Meta-Ebene 1‘. Der Folgerungsbegriff ist insofern eine eigene ‚formale Theorie‘, die über bestimmte ‚Objekte einer tieferen Ebene‘ spricht so wie die abstrakten Begriffe einer Theorie (oder der Alltagssprache) über konkrete Erfahrungstatbestände sprechen. Das Zusammenwirken von Folgerungsbegriff (auf Meta-Ebene 1) und den formalen Ausdrücken als Objekten setzt eine eigene ‚Interpretationsbeziehung‘ (letztlich eine Art von ‚Abbildung‘) voraus, die wiederum auf einer noch anderen Ebene — Meta-Ebene 2 — angesiedelt ist. Diese Interpretationsbeziehung benutzt sowohl die formalen Ausdrücke (mit ihren Wahrheitswerten!) und den Folgerungsbegriff als ‚Objekte‘, um zwischen diesen eine Interpretationsbeziehung zu installieren. Normalerweise wird diese Meta-Ebene 2 von der so gescholtenen Alltagssprache bewältigt und die implizite Interpretationsbeziehung ist ‚in den Köpfen der Mathematiker (eigentlich in den Köpfen der Logiker)‘ verortet, die davon ausgehen, dass ihre ‚Praxis des Folgerns‘ genügend Erfahrungsdaten liefern, um den ‚Inhalt der Bedeutungsbeziehung‘ zu ‚verstehen‘.

Es war Kurt Gödel gewesen [2], der 1931 versucht hat, das ‚intuitive Vorgehen‘ bei Meta-Beweisen selbst auch zu formalisieren (mit Hilfe der berühmten Gödelisierung) und damit die Meta-Ebene 3 wiederum zu einem neuen ‚Objekt‘ gemacht hat, über das man explizit diskutieren kann. Im Anschluss an Gödels Beweis gab es weitere Versuche, diese Meta-Ebene 3 nochmals anders zu formulieren oder gar deine Meta-Ebene 4 zu formalisieren. Doch blieben diese Ansätze bislang ohne klares philosophisches Ergebnis.

Klar scheint nur zu sein, dass die Fähigkeit des menschlichen Gehirns, immer wieder neue Meta-Ebenen zu eröffnen, um damit zuvor formulierte Sachverhalte zu analysieren und zu diskutieren, prinzipiell unbeschränkt ist (nur beschränkt durch die Endlichkeit des Gehirns, dessen Energiezufuhr, die Zeit, und ähnliche materielle Faktoren).

Eine interessante Spezialfrage ist es, ob der formaler Folgerungsbegriff der formalen Mathematik angewendet auf Erfahrungstatsachen einer dynamischen empirischen Welt der spezifischen ‚Welt-Dynamik‘ überhaupt angemessen ist? Für den Bereich der ’scheinbar materiellen Strukturen‘ des Universums hat die moderne Physik vielfache Phänomene geortet, die sich einfach klassischen Konzepten entziehen. Eine ‚Materie‘, die zugleich ‚Energie‘ ist, ist tendenziell eher nicht mehr klassisch beschreibbar, und Quantenphysik ist — bei aller ‚Modernität‘ — letztlich immer noch ein ‚klassisches Denken‘ im Rahmen einer formalen Mathematik, die vom Ansatz her viele Eigenschaften nicht besitzt, die aber der erfahrbaren Welt zukommen.

Diese Begrenztheit eines formal-mathematischen physikalischen Denkens zeigt sich besonders krass am Beispiel jener Phänomene, die wir ‚Leben‘ nennen. Die erfahrungsbasierten Phänomene, die wir mit ‚lebenden (= biologischen) Systemen‘ in Verbindung bringen, sind auf den ersten Blick komplett materielle Strukturen, allerdings haben sie dynamische Eigenschaften, die mehr über die ‚Energie‘ aussagen, die sie hervorruft, als über die Materialität, mittels der sie sich realisieren. Insofern ist die implizite Energie der eigentliche ‚Informationsgehalt‘ von lebenden Systemen, die in ihrer Grundstruktur ‚radikal freie‘ Systeme sind, da Energie als ’nicht begrenzbar‘ erscheint. Die unübersehbare Tendenz lebender Systeme, ‚aus sich heraus‘ immer ‚mehr Komplexität zu ermöglichen‘ und zu integrieren widerspricht allen bekannten physikalischen Prinzipien. Die ‚Entropie‘ wird gerne als Argument benutzt, um diese Form von ‚biologischer Selbstdynamik‘ mit Verweis auf eine simple ‚obere Schranke‘ als ‚begrenzt‘ zu relativieren, doch macht dieser Verweis das originäre Phänomen des ‚Lebendigen‘ damit nicht vollständig zunichte.

Besonders spannend wird es, wenn man es wagt, an dieser Stelle die Frage nach der ‚Wahrheit‘ zu stellen. Lokalisiert man die Bedeutung des Begriffs ‚Wahrheit‘ zunächst mal in der Situation, in der ein biologisches System (hier der Mensch) innerhalb seines Denkens eine gewisse ‚Korrespondenz‘ zwischen seinen abstrakten Begriffen und solchen konkreten Wissensstrukturen herstellen kann, die sich über einen Interaktionsprozess mit Eigenschaften einer erfahrbaren Welt in Verbindung bringen lassen, und zwar nicht nur als einzelnes Individuum, sondern zusammen mit anderen Individuen, dann hat jedes abstrakte Ausdruckssystem (genannt ‚Sprache‘) nur in dem Maße einen ‚wahren Wirklichkeitsbezug‘, als es biologische Systeme gibt, die solche Bezüge herstellen können. Und diese Bezüge hängen weiterhin ab von der Struktur der Wahrnehmung und der Struktur des Denkens dieser Systeme; diese wiederum hängen ab von der Beschaffenheit der Körper als Kontext der Gehirne, und die Körper hängen wiederum sowohl ab von der materiellen Struktur und Dynamik der Umgebung wie auch von den gesellschaftlichen Alltagsprozessen, die weitgehend festlegen, was ein Mitglied einer Gesellschaft erleben, lernen, arbeiten, planen und tun kann. Was immer ein Individuum kann bzw. könnte, die Gesellschaft verstärkt entweder das individuelle Potential oder ‚friert‘ es ein. ‚Wahrheit‘ existiert unter diesen Bedingungen als ein ‚frei beweglicher Parameter‘, der durch die jeweilige Prozessumgebung erheblich beeinflusst wird. Das Reden von ‚kultureller Vielfalt‘ kann eine gefährliche ‚Verniedlichung‘ von massiver Unterdrückung ‚alternativer Lern- und Handlungsprozessen‘ sein, die einer Gesellschaft ‚entzogen‘ werden, weil sie ’sich selbst einsperrt‘. Unwissenheit ist tendenziell kein guter Ratgeber. Wissen als solches garantiert aber auch kein ‚richtiges‘ Handeln. Der ‚Prozess der Freiheit‘ auf dem Planet Erde ist ein ‚galaktisches Experiment‘, dessen Ernsthaftigkeit und Ausmaß bislang kaum gesehen wird.

DER AUTOR

Einen Überblick über alle Beiträge von Autor cagent nach Titeln findet sich HIER.

ANMERKUNGEN

[1] Auf Literaturangaben wird hier verzichtet. Es wären viele hunderte Texte zu erwähnen. Das kann keine Skizze leisten.

[2] Siehe Kurt Gödel, Unvollständigkeitssätze, 1931: https://de.wikipedia.org/wiki/Kurt_G%C3%B6del#Die_Unvollst%C3%A4ndigkeitss%C3%A4tze