VORGESCHICHTE
Für einen Überblick zu allen vorausgehenden Beiträgen dieser rekonstruierenden Lektüre von Avicennas Beitrag zur Logik siehe AVICENNAS ABHANDLUNG ZUR LOGIK – BLITZÜBERSICHT.
WAHRE UND FALSCHE AUSSAGEN
1. Bislang haben wir uns bei der Rekonstruktion vorgetastet von der Wahrheit/ Falschheit von Aussagen A,B, … über zusammengesetzte wahre/ falsche Aussagen zur Feinstruktur von Aussagen der Art (S P). Schon am einfachen Beispiel der Beziehung zwischen zwei Objekten (a ist ein Y) oder (a hat ein Y) wurde die Hypothese formuliert, dass solche Aussagen voraussetzen, dass es in der Objekthierarchie O nicht nur zwei Objekte a,Y gibt, die in Beziehung gesetzt werden können, sondern dass es grundsätzlich möglich ist, ganze allgemein ‚Beziehungen‘ [R] (Relationen) zwischen Teilen der Objekthierarchie zu identifizieren und dann zu benennen.
2. Damit stellt sich die Frage, welche Arten von Beziehungen in der angenommenen Objekthierarchie O angenommen werden können/ müssen.
BEZIEHUNGSRAUM – TRANSZENDENTALE BEDINGUNGEN
3. IST_EIN, HAT_Y: Grundsätzlich folgt aus der Annahme einer ‚Hierarchie‘ im Objektraum O, dass es zwischen den Elementen der verschiedenen ‚Ebenen’/ ‚Stufen‘ (engl.: ‚level‘, ‚layer‘,…) die Beziehung gibt, dass die Objekte auf den ’niedrigeren‘ Stufen rein definitorisch/ analytisch die ‚Elemente‘ der höheren Stufen sind. Diese Arten von Beziehungen sind daher ein ‚Abfallprodukt‘ der vorgegebenen hierarchischen Struktur. Als solche sind diese Beziehungen ’notwendig‘, allerdings in einem grundlegenden Sinne: sie sind unumgänglich dem Denken vorgegeben, als Strukturmerkmal des Denkens. Dafür würde ich hier gerne Kants Begriff der ‚transzendentalen‘ Struktur benutzen, die er in seinem Hauptwerk Kritik der reinen Vernunft beschrieben hat. Diese dem Denken kraft Struktur vorgegebenen Gegebenheiten sind ‚transzendental‘. Im Lichte der modernen Evolutionsforschung sind es jene Strukturen, die genetisch mitbedingt die Strukturen unseres Körpers und unseres Gehirns ‚festlegen‘ und damit gewisse Arten der Informationsverarbeitung ermöglichen bzw. ausschließen (was schon Konrad Lorenz in seinem Buch ‚Die Rückseite des Spiegels‘ beschrieben hat (trotz seiner Nähe zu nationalsozialistischem Gedankengut)).
4. Es fragt sich hier, welch weitere Beziehungen/ Relationen man annehmen muss. Avicenna selbst deutet schon hin auf die Aspekte ‚Anzahl‘, ‚Raum‘ und ‚Zeit‘.
ANZAHL – QUANTITÄT
5. Der Aspekt der Anzahl ergibt sich transzendental daraus, dass ein Gattungsobjekt mehr als eine Instanz haben kann. Und insoweit überhaupt Begriffe ‚über‘ (meta) die Objekthierarchie möglich sind, wäre der Begriff der ‚Anzahl‘ (‚Quantität‘) vergleichsweise einfach. Entsprechend der Idee der ‚induktiven Aufzählung‘ wie bei der Definition der ’natürlichen Zahlen‘ kann man sehr feingliedrige ‚Äquivalenzklassen‘ bilden zwischen einer natürlichen Zahl und der entsprechenden Menge der Instanzen. Für den ‚Normalfall‘ genügen aber Begriffe wie ‚alle‘, ‚einige als nicht alle‘ sowie ‚keine‘ als ’nicht einige‘. In diesem Sinne wäre der ‚Anzahlbegriff‘ immer ‚lokal‘ bezogen auf die Instanzen eines Gattungsbegriffs. Geschrieben $latex \forall$ (alle), $latex \neg\forall$ (nicht alle = einige) und $latex \neg\exists$ (nicht einige als keine).
6. Entsprechend könnte man schreiben: $latex \forall (x \in S)(S P)$ als ‚Für alle Elemente aus S gilt, dass P für S gilt‘; $latex \neg\forall (x \in S)(S P)$ als ‚Nicht für alle x aus S gilt, dass P auf S zutrifft‘ bzw. ‚Für einige x aus S gilt, dass P auf S nicht zutrifft‘. $latex \neg\exists (x \in S)(S P)$ Es gibt kein x aus S, so dass P auf S zutrifft.
ZEIT
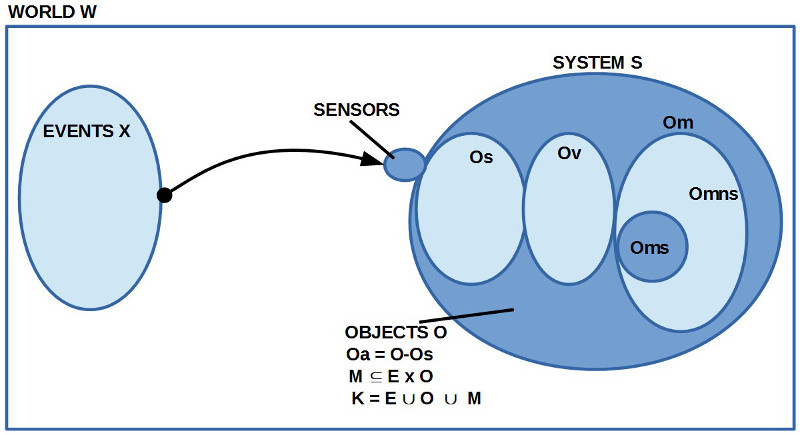
7. Der Aspekt der ‚Zeit‘ ergibt sich transzendental dann, wenn man davon ausgeht, dass unsere Objekthierarchie (siehe Schaubild) einen Gedächtnisanteil hat, aufgrund dessen Ereignisse als ‚vergangen‘, als ‚vorher‘ klassifiziert werden können. Der Begriff der ‚Zeit‘ ist dann eine ‚lineare‘ Anordnung von Ereignissen geordnet mit ‚vorher‘ ($latex <$) und ’nachher‘ ($latex >$) oder ‚gleichzeitig‘ ($latex =$). Auch hier funktionieren grobe Begriffe wie ‚immer‘ und ‚manchmal‘ oder ’nie‘ (nach Bedarf – wie bei der Anzahl – beliebig verfeinerbar durch ‚Uhren‘).
8. Beispiele: $latex \forall (t \in T)(S(t) P)$ als ‚Für alle Zeitpunkte t gilt, dass P auf S zutrifft‘, oder ‚P trifft auf S immer zu‘; $latex \neg\forall (t \in T)(S(t) P)$ als ‚Nicht für alle Zeitpunkte trifft P auf S zu‘ oder ‚Nicht immer …‘ oder ‚Manchmal trifft P nicht auf S zu‘; $latex \neg\exists (t \in T)(S P)$ als ‚Es gibt keinen Zeitpunkt t, bei dem P auf S zutrifft‘ oder ‚Niemals trifft …‘.
9. Im Fall der Zeit gibt es neben den allgemeinen Quantoren ‚immer‘, ‚manchmal‘ und ’nie‘ auch lokale Zeitangaben wie ‚VOR‘, ‚NACH‘, ‚GESTERN‘, ‚HEUTE’… Einige dieser lokalen Begriffe (‚HEUTE‘, ‚GESTERN‘, ..) setzen einen Standunkt voraus, andere (‚VOR‘, ‚NACH‘, …) nicht. ‚VOR dem Spiel regnete es‘ beschreibt die zeitliche Beziehung zwischen ‚Spiel‘ und ‚regnen‘ unabhängig vom Standpunkt. ‚GESTERN traf Hans Inge‘ ist vollständig nur verstehbar, wenn man den Zeitpunkt der Aussage kennt.
RAUM
10. Der Aspekt des ‚Raumes‘ ergibt sich dann transzendental, wenn man davon ausgeht, dass alle sinnlichen Eindrücke immer ‚eingebettet‘ in eine Raumstruktur auftreten; es gibt keinen Eindruck ohne eine ‚räumliche Umgebung‘ (siehe allgemeine Annahme der Einbettung von S in W). Auch der Begriff des ‚echten Objektes‘ a setzt voraus, dass sich das ‚a‘ von einer ‚Umgebung‘ abgrenzen lässt. Eine offene Frage ist, wie genau sich diese implizite Raumstruktur aus der Sinneswahrnehmung in der Objekthierarchie O abbildet.
11. Von Avicenna haben wir schon gelesen, dass er Raumbeziehungen wie ‚a IST_IN b‘ kennt, oder ‚a IST_VOR b‘, usw. Unterstellt man – als Arbeitshypothese – dass alle Objekt implizit (und transzendental) sowohl in der Wahrnehmung wie auch in der repräsentierenden Objekthierarchie generell in einem mindestens drei-dimensionalen (imaginären) Raum vorkommen, dann würde sich daraus ergeben, dass Beziehungen wie ‚_IN_‘, ‚_AUF_‘, ‚_VOR_‘, ‚_DRUNTER_‘ usw. generell zur Verfügung stehen. Implizit setzen sie dann möglicherweise immer (?) einen Betrachtungsstandpunkt voraus (eine ‚Orientierung‘), von wo aus auf die Objekte ‚geschaut‘ wird: ‚_LINKS_‘ ist eben nur unter Berücksichtigung der Betrachterposition eindeutig. Als Arbeitshypothese soll hier angenommen werden, dass alle Raumbeziehungen eine Betrachterposition voraussetzen. Ob und wie diese im ‚Redekontext‘ spezifiziert wird, liegt außerhalb der Raumbeziehung.
12. Im Fall des Raumes kann man aber auch – wie schon bei Anzahl und Zeit – grobe Angaben unterscheiden und detaillierte: man kann auch im Fall des Raumes reden von ‚überall‘, ’nirgend‘ oder ‚an einigen‘. $latex \forall (r \in R)(S P)$ als ‚An allen Raumpunkten trifft P auf S zu‘ oder ‚Überall trifft …‘; $latex \neg\forall (r \in R)(S P)$ als ‚Nicht an allen Raumpunkten …‘ als ‚An einigen Raumpunkten …‘; $latex \neg\exists (r \in R)(S P)$ als ‚es gibt keinen Raumpunkt, an dem P auf S zurifft‘ als ‚Nirgends gibt es …‘.
13. Zwischen ‚allgemeinen‘ Raumangaben und ‚lokalen‘ Raumangaben kann es aber offensichtlich Kombinationen geben, z.B. ‚Überall gilt, dass a nicht AUF b STEHT‘, $latex \forall (r \in R)(a \neg\ AUF\ b)$. In diesem Fall ist S und P vertauscht! ‚a STEHT nicht AUF‘ ist das Prädikat P, und ‚b‘ ist das Subjekt S, also P S). ‚An manchen Stellen gilt, dass a UNTER b LIEGT‘ als $latex \exists (r \in R)(a LIEGT UNTER b)$. Auch hier ist S und P vertauscht $latex \exists (r \in R)(P S)$.
WECHSELWIRKUNG ZWISCHEN ANZAHL, RAUM und ZEIT
14. Zwischen den Aspekten ‚Anzahl‘, ‚Zeit‘ und ‚Raum‘ kann es Interaktionen geben.
15. Eine Aussage wie ‚ALLE Raben sind schwarz‘ verändert sich mit der Angabe eines Raumgebietes ‚ALLE Raben IM GEBIET X sind schwarz‘; oder durch Hinzufügung des Aspektes der Zeit: ‚FRÜHER waren ALLE Raben IM GEBIET X schwarz‘.
16. Entsprechend wird eine Aussage wie ‚ÜBERALL gibt es Bäume‘ verändert durch ‚ÜBERALL gibt es EINIGE Bäume‘ und ‚FRÜHER gab es ÜBERALL EINIGE Bäume‘. Letzte Aussagen könnte man formalisieren: $latex FRUEHER\ \forall (r \in R)\exists (s \in S)(S gibt es)$. Die Zeitangabe ‚FRUEHER‘ ist letztlich auch ein Quantor, den man über die Zeitachse definieren muss.
ERGEBNISSE
17. Die kurze Betrachtung zeigt, dass es mindestens die drei großen Aspekte ‚Anzahl‘, ‚Zeit‘ und ‚Raum‘ gibt, die entweder als Quantoren darstellbar sind oder als ‚lokale‘ Beziehungen. Eine Wechselwirkung ist problemlos, da alle drei Aspekte voneinander ‚unabhängig‘ sind. Man muss nur darauf achten, dass im Einzelfall immer klar ist, wie die Zuordnung von Raumgebiet, Zeitabschnitt und Objektanzahl gedacht ist. Zu sagen ‚ALLE Menschen sind klein und ALLE Menschen sind groß‘ klingt widersinng, aber zu sagen ‚IM RAUMGEBIET X sind ALLE Menschen klein und IM RAUMGEBIET Y sind ALLE Menschen groß‘ macht Sinn.
18. Die transzendentale Gegebenheit der Aspekte Anzahl, Raum und Zeit impliziert eine Reihe von ‚Einschränkungen‘, die in einer vollständigen Rekonstruktion ausdrücklich zu beschreiben wären.
Fortsetzung folgt
QUELLEN
- Avicenna, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
- Digital Averroes Research Environment
- Immanuel Kant, Critik der reinen Vernunft‘, Riga, 1781
- Konrad Lorenz, 1973, ‚Die Rückseite des Spiegels. Versuch einer Naturgeschichte des menschlichen Erkennens‘, München, Zürich: Piper
- Nicholas Rescher (1928 – ),The Development of Arabic Logic. University of Pittsburgh Press, 1964
- Hans-Jörg Sandkühler (Hg.) unter Mitwirkung von Dagmar Borchers, Arnim Regenbogen, Volker Schürmann und Pirmin Stekeler-Weithofer, ‚Enzyklopädie Philosophie‘, 3 Bd., Hamburg: FELIX MEINER VERLAG, 2010 (mit CD-ROM)
- Stanford Encyclopedia of Philosophy, Aristotle’s Logic
- Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
- Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
- Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
- Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7
Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER