Journal: Philosophie Jetzt – Menschenbild, ISSN 2365-5062, 9.Oktober 2014
URL: cognitiveagent.org
Email: info@cognitiveagent.org

Autor: Gerd Doeben-Henisch
Email: gerd@doeben-henisch.de

VORGESCHICHTE

Für einen Überblick zu allen vorausgehenden Beiträgen dieser rekonstruierenden Lektüre von Avicennas Beitrag zur Logik siehe AVICENNAS ABHANDLUNG ZUR LOGIK – BLITZÜBERSICHT.

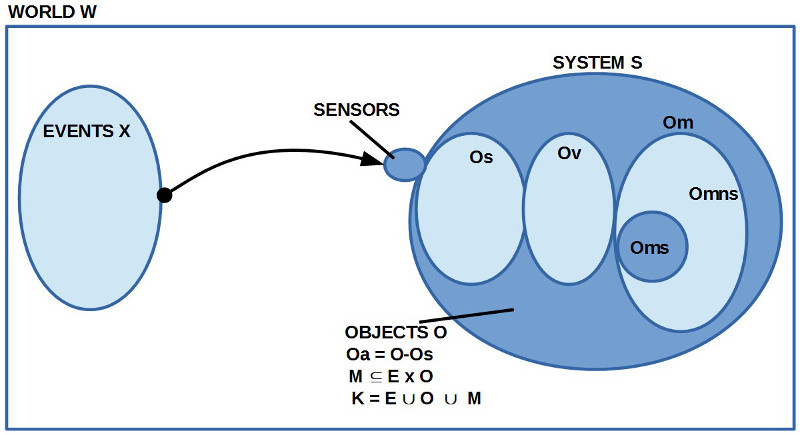
FIGUR 1 MIT DEN QUANTOREN A(A-)(A-)

1. Für diese Figur benutzt Avicenna die Muster ‚A F ist B‘, ‚A B ist nicht H‘ als ‚Kein A ist B‘, ‚A F ist nicht H‘ als ‚Kein F ist H‘, dazu die Beispiele ‚Jeder ausgedehnte Körper ist farbig‘, ‚Kein farbiger Körper ist unerschaffen‘, ‚Kein ausgedehnter Körper ist unerschaffen‘.

2. Wir haben als echte Objekte die ‚Körper‘ mit der zusätzlichen Eigenschaft, ‚ausgedehnt‘, dies ergibt die Menge F := ‚ausgedehnte Körper‘. Im Falle des Terms ‚B‘ wird es schwierig. In dem Ausdruck ‚Kein farbiger Körper ist unerschaffen‘ repräsentiert ‚farbige Körper‘ ein B‘ als die Menge der ‚farbigen Körper‘; im Ausdruck ‚Jeder ausgedehnte Körper ist farbig‘ (A F ist B) steht der Termin ‚B‘ aber für eine Eigenschaft ‚farbig‘ eingebettet in eine Zuschreibungsbeziehung ‚ist‘, so dass – implizit — gesagt wird, dass alle Elemente aus der Menge F die Eigenschaft haben, ‚farbig zu sein‘. Wir haben also B=’farbig‘ und B’=’farbige Körper‘. Im direkten Vergleich ist B und B‘ nicht gleich! Man kann zwar aus (A F ist B) folgern, dass gilt ‚Jeder ausgedehnte Körper ist ein farbiger Körper‘, aber das hat Avicenna nicht explizit hingeschrieben. Explizit müsste man schreiben (A F ist B) mit B := ‚farbig‘, (A F sind B‘) mit B‘ := ‚farbige Körper‘, und dann (A B‘ nicht sind H), dann (A F nicht sind H).

3. Im Fall des Ausdrucks ‚Kein farbiger Körper ist unerschaffen‘, also (A B‘ ist nicht H) benutzt Avicenna ‚unerschaffen‘ wieder als Eigenschaft. Der Ausdruck ‚erschaffen‘ ist ursprünglich eine Tätigkeit, die eine Beziehung zwischen Objekten bezeichnet, üblicherweise als ‚X erschafft Y‘ mit der Umformung ‚Y wurde (von X) erschaffen‘. Die Verneinung wäre (Nicht ‚Y wurde (von X) erschaffen‘), geschrieben als ‚Y wurde (von X) nicht erschaffen‘, was umgeformt werden kann in die Eigenschaft ‚unerschaffen‘, ‚Y ist unerschaffen‘. Y ist dann ein echtes Objekt mit der Eigenschaft ‚unerschaffen‘.

4. Im Ausdruck ‚Kein farbiger Körper ist unerschaffen‘ wird also eine Beziehung hergestellt zwischen der Menge der farbigen Körper (B‘) und der Eigenschaft ‚unerschaffen‘ zu sein. Diese Beziehung ist ’negativ‘, insoweit gesagt wird, dass kein Element aus der Menge der ‚farbigen Körper‘ B1 die Eigenschaft ‚unerschaffen‘ H haben soll.

5. Damit haben wir in den ersten beiden Ausdrücken dieses Musters des Syllogismus zweimal das Schema, dass es ein echtes Objekt gibt, und in einem Fall wird den Elementen des Objektes eine bestimmte Eigenschaft zugesprochen (Alle F … sind …), im anderen Fall wird eine Eigenschaft abgesprochen (Alle B‘ …. nicht sind …).

6. Zusätzlich wird (implizit) eine Enthaltensbeziehung festgestellt im Sinne von ‚Jeder ausgedehnte Körper ist farbig‘ und ‚Kein farbiger Körper ist unerschaffen‘: $latex F \subseteq B’$, $latex B1 \subseteq \overline{H‘}$. Daraus folgt ‚analytisch‘, dass gilt $latex F \subseteq \overline{H‘}$.

OBJEKTIFIZIERUNG, ENTHALTENSEIN, ZUSCHREIBUNG, VERERBUNG, QUANTOREN

7. Wir treffen in diesem Muster mit den Beispielen wieder auf den Prozess der Objektifizierung, tatsächlich sogar in impliziten Formen mit der expliziten Angabe von Eigenschaften und der stillschweigenden Annahme einer daraus sich ergebenden Mengenbildung.

8. Zusätzlich finden sich wieder Enthaltensbeziehungen einerseits anhand von Eigenschaftszuschreibungen, andererseits durch Benutzung von Anzahlquantoren.

9. Die Zuschreibung von Eigenschaften wird explizit vorgenommen.

10. Eine Vererbung von Eigenschaften von einer Menge zur anderen tritt nur implizit über eine Enthaltensbeziehung auf.

11. Es tritt nur eine Sorte von Quantoren auf.

12. Auch sei angemerkt, dass außer der Negation kein weiterer aussagenlogischer Operator auftritt.

Fortsetzung folgt

QUELLEN

• Avicenna, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
• Digital Averroes Research Environment
• Immanuel Kant, Critik der reinen Vernunft‘, Riga, 1781
• Konrad Lorenz, 1973, ‚Die Rückseite des Spiegels. Versuch einer Naturgeschichte des menschlichen Erkennens‘, München, Zürich: Piper
• Nicholas Rescher (1928 – ),The Development of Arabic Logic. University of Pittsburgh Press, 1964
• Hans-Jörg Sandkühler (Hg.) unter Mitwirkung von Dagmar Borchers, Arnim Regenbogen, Volker Schürmann und Pirmin Stekeler-Weithofer, ‚Enzyklopädie Philosophie‘, 3 Bd., Hamburg: FELIX MEINER VERLAG, 2010 (mit CD-ROM)
• Stanford Encyclopedia of Philosophy, Aristotle’s Logic
• Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
• Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
• Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
• Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7

Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER