AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 21
VORGESCHICHTE
Für einen Überblick zu allen vorausgehenden Beiträgen dieser rekonstruierenden Lektüre von Avicennas Beitrag zur Logik siehe AVICENNAS ABHANDLUNG ZUR LOGIK – BLITZÜBERSICHT.
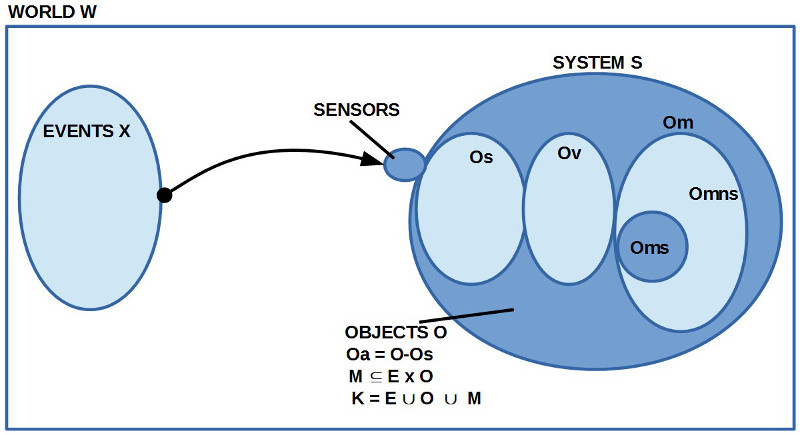
FIGUR 1, MUSTER 3, MIT DEN QUANTOREN EAE
1. Für diese Figur benutzt Avicenna die Ausdrücke ‚E S sind G‘, ‚A G haben F‘, ‚E S haben F‘. Dazu die Beispiele ‚Einige Substanzen sind Geister‘, ‚Alle Geister haben eine Form‘, ‚Einige Substanzen haben eine Form‘.
2. Wie immer unterstellen wir zunächst eine abstrakte Bedeutung repräsentiert in der unterstellten dynamischen Objektstruktur Oa, losgelöst von der Frage der empirischen Geltung.
3. Die Zuordnung von Muster (E S sind G) zum Ausdruck ‚Einige Substanzen sind Geister‘ ergibt die Abkürzungen ‚E := Einige‘, ‚S := Substanzen‘, ‚G := Geister‘.
4. ‚S‘ und ‚G‘ repräsentieren echte Objekte und lassen sich damit als Mengen von potentiellen Elementen darstellen mit der Aussage, dass es Elemente gibt, die in beiden potentiellen Mengen vorkommen, also z.B. $latex S \cap G \not= \emptyset$.
5. Die Zuordnung von Muster (A G haben F) zum Ausdruck ‚Alle Geister haben eine Form‘ ergibt die Abkürzungen ‚A := Alle‘, ‚G := Geister‘, und ‚F := Form‘.
6. In diesem Beispiel liegt wieder der Fall vor, dass mit dem Term ‚F‘ als ‚Form‘ hier ein ‚unechtes‘ Objekt, also eine ‚Eigenschaft‘ vorliegt, was auch durch das Beziehungswort ‚haben‘ ausgedrückt wird. Man würde also sagen müssen, dass alle G die Eigenschaft haben, eine Form ‚F‘ zu besitzen, oder noch ausdrücklicher: alle potentiellen Elemente der Menge G (Geister) haben auch die Eigenschaft, eine Form ‚F‘ zu besitzen. Da Eigenschaften nie alleine auftreten können, könnte man hier interpolieren und sagen, es gibt eine ein unbekanntes Objekt, dessen potentiellen Elemente die Eigenschaft besitzen, eine Form zu sein. Dann gibt es die Menge der Objekte, die eine Form haben; nennen wir diese abkürzend F‘. Dann könnte man sagen, dass alle potentiellen Elemente von G auch potentielle Elemente von F‘ sind, also etwa $latex G \subseteq F’$. Oder man belässt es bei der einfachen Zuweisung einer weiteren Eigenschaft F im Sinne von $latex \forall x(G(x) \longrightarrow F(x))$. Diese Formulierung zeigt, dass wir sprachlich quasi automatisch die Mitgliedschaft in einer Menge G so interpretieren, als ob das Element x das in G ist, die ‚Eigenschaft G habe‘. So, wie wir umgekehrt aus dem ‚haben einer Eigenschaft F‘ auf die ‚Elementschaft in einer potentiellen Menge F‘ schließen. Dies kann man als ein ‚Indiz‘ dafür sehen, dass es sich mit den angenommenen ‚echten‘ und ‚unechten‘ Objekten um einen tiefliegenden (transzendentalen) Mechanismus des Alltagsdenkens handelt.
7. Wenn also gelten soll, dass einige Elemente von der potentiellen Menge S auch Elemente der potentiellen Menge G sind, zugleich aber alle Elemente der potentiellen Menge G die Eigenschaft F haben (bzw. in der Menge der potentiellen Elemente von F‘ sind), dann ‚vererbt‘ sich diese Eigenschaft auch auf einige Elemente der potentiellen Menge von S, also ‚Einige Substanzen haben eine Form‘ bzw. mit ‚E:=Einige‘, ‚S:=Substanzen‘ und ‚F:=Form‘ dann (E S haben F).
8. Die Argumentation basiert wieder auf dem Vorhandensein von Mengenrepräsentationen, dem Enthaltensein in diesen Mengen mit den Anzahlverhältnissen, sowie der ‚Vererbung‘ aufgrund von vorhandenen ‚Zuschreibungen‘.
FIGUR 1, MUSTER 4, MIT DEN QUANTOREN E(A-)(E-)
9. Für diese Figur benutzt Avicenna die Ausdrücke ‚E S sind G‘, ‚A G nicht haben B‘, ‚E S nicht haben B‘. Dazu die Beispiele ‚Einige Substanzen sind Geister‘, ‚Alle Geister haben keinen Körper‘ (als: ‚Kein Geist hat einen Körper‘), ‚Einige Substanzen haben keinen Körper‘.
10. Die Zuordnung von Muster (E S sind G) zum Ausdruck ‚Einige Substanzen sind Geister‘ ergibt die Abkürzungen ‚E := Einige‘, ‚S := Substanzen‘, ‚G := Geister‘.
11. ‚S‘ und ‚G‘ repräsentieren echte Objekte und lassen sich damit als Mengen von potentiellen Elementen darstellen mit der Aussage, dass es Elemente gibt, die in beiden potentiellen Mengen vorkommen, also z.B. $latex S \cap G \not= \emptyset$.
12. Die Zuordnung von Muster (A G nicht haben B) zum Ausdruck ‚Alle Geister nicht haben einen Körper‘ (mit ’nicht haben einen‘ als ‚haben keinen‘) ergibt die Abkürzungen ‚A := Alle‘, ‚G := Geister‘, und ‚B := Körper‘.
13. In diesem Beispiel liegt wieder der Fall vor, dass mit dem Term ‚B‘ als ‚Körper‘ hier ein ‚unechtes‘ Objekt vorliegt, das als ‚Eigenschaft‘ dem Objekt G zugesprochen wird. Andererseits wird der Term ‚Körper‘ oft auch als echtes Objekt im Sinne von ‚der Körper da‘ verwendet (In der englischen Übersetzung wird die Verwendung als echtes Objekt benutzt; ich weiß nicht, was im Urtext steht. Letztlich spielt es keine entscheidende Rolle. Wie wir lernen: echte und unechte Objekte können sich wechselseitig leicht ’substituieren‘). Würde man aus der Eigenschaft ‚Körper‘ ein Objekt Körper B‘ machen, dann hätten wir die Verhältnisse $latex G \subseteq B’$. Würden wir mehr den Eigenschaftscharakter betonen, dann bliebe es bei $latex \forall x(G(x) \longrightarrow B(x))$.
14. ‚E S sind G‘, ‚A G nicht haben B‘, ‚E S nicht haben B‘.
15. Wenn also gelten soll, dass einige Elemente von der potentiellen Menge S auch Elemente der potentiellen Menge G sind, zugleich aber alle Elemente der potentiellen Menge G nicht die Eigenschaft B haben (bzw. nicht in der Menge der potentiellen Elemente von B‘ sind), dann ‚vererbt‘ sich diese Eigenschaft auch auf einige Elemente der potentiellen Menge von S, also ‚Einige Substanzen haben keinen Körper‘ bzw. mit ‚E:=Einige‘, ‚S:=Substanzen‘ und ‚B:=Körper‘ dann (E S nicht haben B).
16. Die Argumentation basiert wieder auf dem Vorhandensein von Mengenrepräsentationen, dem Enthaltensein in diesen Mengen mit den Anzahlverhältnissen, sowie der ‚Vererbung‘ aufgrund von vorhandenen ‚Zuschreibungen‘.
ZUSAMMENFASSUNG SYLOGISMUS FIGUR 1, MUSTER 1-4
17. Betrachten wir alle vier Muster von Figur 1.
| 1 | 2 | 3 | 4 | |
| Annahme 1 | A | A | E | E |
| Annahme 2 | A | A- | A | A- |
| Folgerung | A | A- | E | E- |
18. Die Prämissen haben die Form (AA), (A(A-)),(EA), (E(A-)). Von der Mengenstruktur her betrachtet, die sich über die Objektzuordnung ergibt, zeigt sich hier (i) das Verhältnis, dass Entweder Alle (A) Elemente der Ausgangsmenge (Nebenannahme, Minor) auch in der zweiten Menge (Hauptannahme, Major) sind oder nur Einige (E). Dann wird die Eigenschaftszuweisung für die zweite Menge (Major) festgelegt: (ii) Entweder haben alle (A) Elemente eine bestimmte Eigenschaft X oder ‚Alle nicht‘ (A-) bzw. ‚keines‘. In der nachfolgenden Folgerung (iii) lässt sich dann mittels ‚Vererbung‘ sagen, dass alle Elemente aus der zweiten Menge (Major), die eine Eigenschaft X haben entweder entsprechend sich auch auf alle (A) oder einige (E) Elemente der ersten Menge (Minor) vererben. Im negativen Fall, wenn kein Element (A-) aus der zweiten Menge (Major) die Eigenschaft X hat, entsprechend nicht. So gesehen repräsentiert die zweite Annahme (Major) tatsächlich den zentralen Sachverhalt. Die erste Annahme (Minor) erscheint dann wie eine Art ‚Filter‘ des zweiten Sachverhalts.
19. Man kann sich jetzt die Frage stellen, ob dies alle Muster sind, die mit der Figur 1 möglich sind oder nicht. Zur Erinnerung hier nochmals die Strukturen der drei Schlussfiguren:
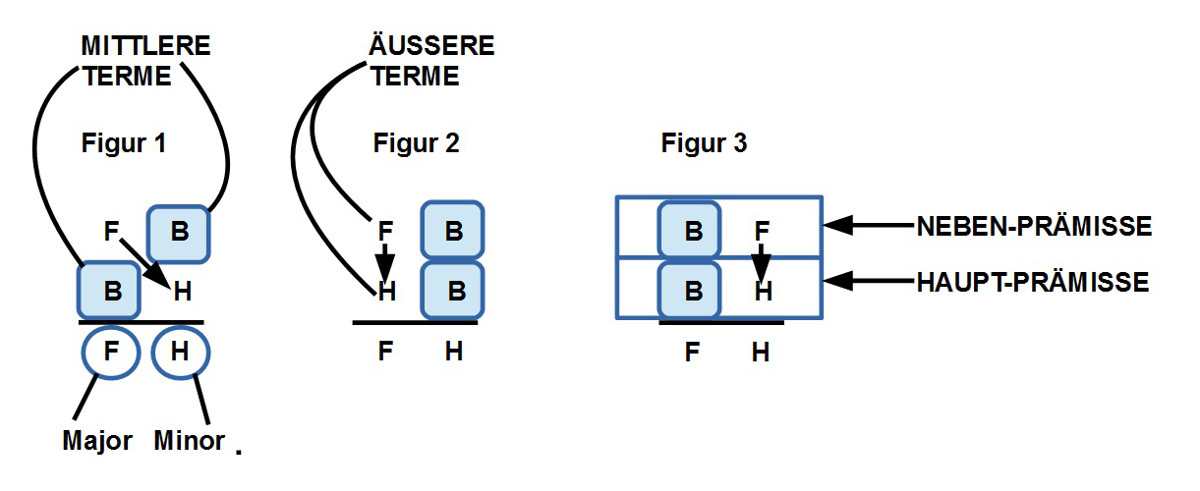
20. Man sieht, dass die drei Figuren sich nur darin unterscheiden, wie die verbindenden Termine zwischen der ersten und zweiten Prämisse verteilt sind: (i) diagonal2, (ii) vertikal rechts, (iii) vertikal links.
21. Würde man die beiden Prämissen vertauschen, würde aus diagonal2 die Anordnung diagonal1. Inhaltlich würde dies keinen Unterschied machen.
22. Die Anordnung vertikal rechts bzw. vertikal links unterscheidet sich formal darin, dass die Aussagestruktur ’normalerweise‘ als (S P) angenommen wird, also links ein Objekt, von dem der Sachverhalt P ausgesagt wird, wobei der Sachverhalt P sehr oft die Zuweisung einer Eigenschaft ist (‚hat einen Körper‘, ‚hat eine Form‘, ‚ist sterblich‘, usw.). Nimmt man dies an, dann würde mit ‚vertikal links‘ bzw. ‚vertikal rechts‘ zwei unterschiedliche Sachverhalte markiert. Wie wir aber an den Beispielen schon gesehen haben, ist der Charakterisierung als P bzw. S ‚fließend‘: man kann (immer?) ein P als S interpretieren und ein S als P. Damit würde die Unterscheidung von ‚vertikal rechts‘ bzw. ‚vertikal links‘ hinfällig. Damit würde alles, was für Figur 2 gilt, auch für Figur 3 zutreffen. Genauso könnte man aufgrund des ‚fließenden‘ Charakters von S und P die Frage stellen, inwieweit die Unterscheidung von Figur 1 zum Unterschied von 2 und 3 aufrecht erhalten werden kann.
23. Die Arbeitshypothese würde hier also lauten: Figur 1 = Figur 2 = Figur 3 bezogen auf die zugrundeliegenden Bedeutungsstrukturen. Dies würde bedeuten, dass die Quantorenkombinationen der drei Figuren ‚gleich möglich‘ sein sollten. Dies soll in den nächsten Beiträgen überprüft werden.
Fortsetzung folgt
QUELLEN
- Avicenna, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
- Digital Averroes Research Environment
- Immanuel Kant, Critik der reinen Vernunft‘, Riga, 1781
- Konrad Lorenz, 1973, ‚Die Rückseite des Spiegels. Versuch einer Naturgeschichte des menschlichen Erkennens‘, München, Zürich: Piper
- Nicholas Rescher (1928 – ),The Development of Arabic Logic. University of Pittsburgh Press, 1964
- Hans-Jörg Sandkühler (Hg.) unter Mitwirkung von Dagmar Borchers, Arnim Regenbogen, Volker Schürmann und Pirmin Stekeler-Weithofer, ‚Enzyklopädie Philosophie‘, 3 Bd., Hamburg: FELIX MEINER VERLAG, 2010 (mit CD-ROM)
- Stanford Encyclopedia of Philosophy, Aristotle’s Logic
- Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
- Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
- Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
- Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7
Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER