(Letzte Änderung 14.Okt.2014, 06:11h )

Da die rekonstruierende Lektüre zu Avicennas Abhandlung zur Logik ein immer größeres Ausmaß annimmt, erweist sich die Methode, jeden einzelnen Beitrag mit einem Überblick über die vorausgehenden Beiträge einzuleiten, als immer weniger praktikabel. Deswegen wird jetzt ein eigener Blogeintrag als Referenzpunkt für diesen Überblick gewählt. Dies bedeutet, dass künftig alle nachfolgenden Beiträge einleitend (für die ‚Vorgeschichte‘), auf diesen Blogeintrag verweisen werden. Es ist zu beachten, dass diese Übersicht nur eine Übersicht über die wichtigsten Begriffe und Themen ist ohne alle Details und normalerweise auch ohne die ausführliche Diskussion von Avicennas Gedanken. Diese finden sich nur in den Blogeinträgen selbst, auf die verwiesen wird.

1. In einem ersten Beitrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 1 hatte ich geschildert, wie ich zur Lektüre des Textes von Avicenna gekommen bin und wie der Text grob einzuordnen ist.

2. In einem zweiten Beitrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 2 ging es um die Frage, warum überhaupt Logik? Avicenna führt erste Unterscheidungen zu verschiedenen Wissensformen ein, lässt aber alle Detailfragen noch weitgehend im Dunkeln.

3. Im Teil AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 3 ging es um einfache und zusammengesetzte Begriffe, und bei den einfachen Begriffen um ‚individuelle‘ und ‚universelle‘. Schon hier zeigt sich der fundamentale Unterschied zwischen der antiken und der modernen-formalen Logik. In der antiken Logik wird die Ausdrucksebene E – und einer sich daran manifestierenden Folgerungslogik – immer in Verbindung mit einer zugehörigen Bedeutungsstruktur gesehen, die sich an einer Objektstruktur O festmacht. Die moderne formale Logik kennt zwar auch ‚Semantiken‘ und ‚Ontologien‘, diese sind aber ’sekundär‘, d.h. es werden nur solche ‚formalen Semantiken‘ betrachtet, die zum vorausgesetzten syntaktischen Folgerungsbegriff ‚passen‘. Dies sollte dann später an konkreten Beispielen diskutiert werden. Hier liegt der Fokus auf der antiken Logik im Sinne Avicennas.

4. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 4 knüpft Avicenna an den zuvor eingeführten Begriff des ‚universellen‘ Begriffs an und betrachtet jetzt solche als ‚universell‘ bezeichneten Ausdrücke in einem Ausdruckskontext von aufeinanderfolgenden Ausdrücken. Alle diese Ausdrücke könnte man im Sinne der antiken Logik auch als ‚Urteile‘ bezeichnen, durch die einem bestimmten Ausdruck durch andere Ausdrücke bestimmte Bedeutungen (Eigenschaften) zu- oder abgesprochen werden. Hier unterscheidet er die Fälle eines ‚wesentlichen‘ Zusammenhanges zwischen zwei Begriffen und eines ’nicht wesentlichen‘ – sprich ‚akzidentellen‘ – Zusammenhangs.

5. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 5 führt Avicenna eine Reihe von neuen technischen Begriffen ein, die sich nicht alle in ihrer Bedeutung widerspruchsfrei auflösen lassen. Es handelt sich um die Begriffe ‚Genus‘, ‚Spezies‘, Differenz, allgemeine und spezielle Akzidens, den Begriff ‚Kategorie(n)‘ mit den Kategorien ‚Substanz‘, ‚Qualität‘ und ‚Quantität‘. Die Rekonstruktion führt dennoch zu spannenden Themen, z.B. zu einem möglichen Einstieg in das weltverändernde Phänomen der kognitiven Evolution.

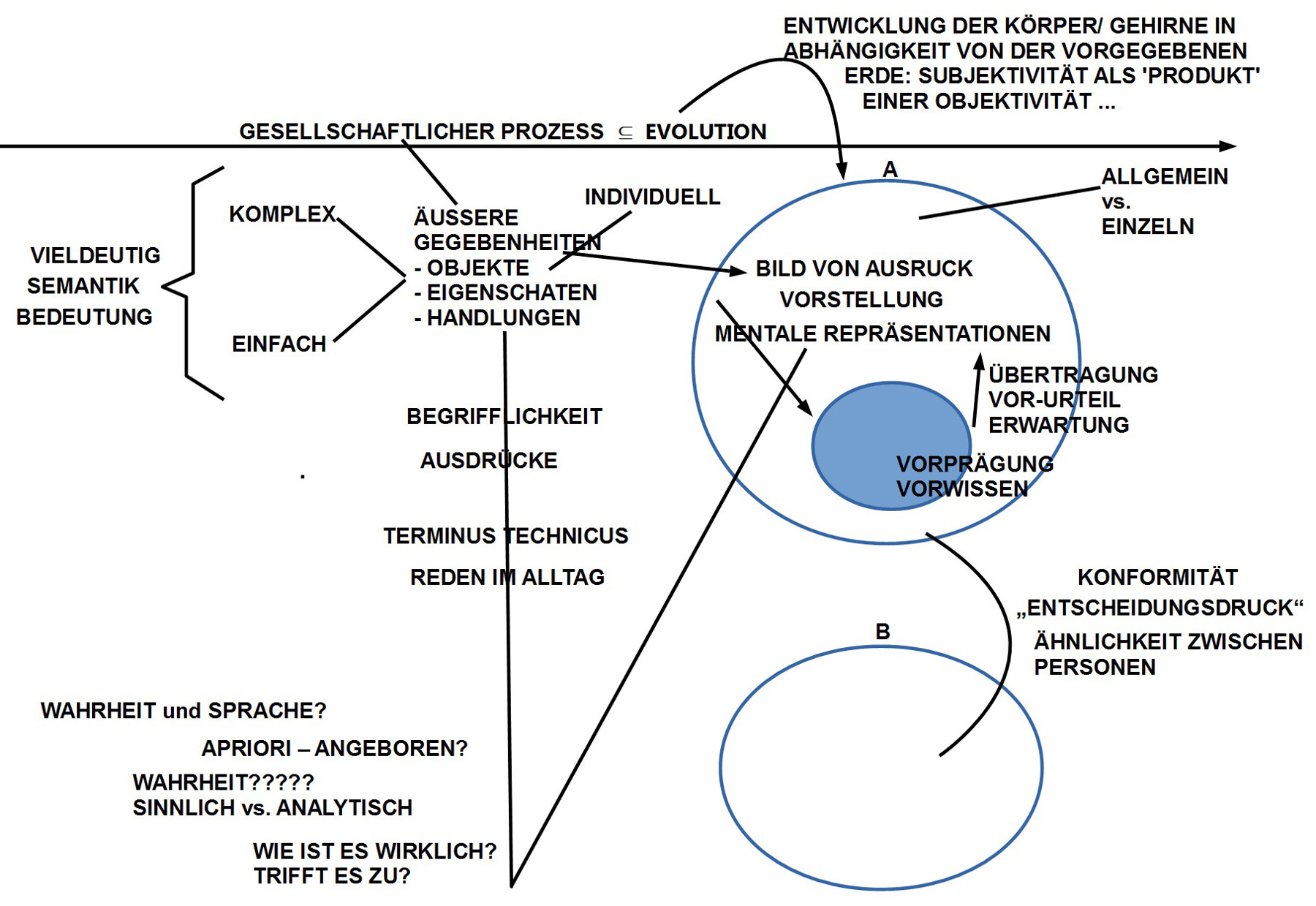
6. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 6 geht es um die Begriffe ‚Definition‘ und ‚Beschreibung‘. Im Verhältnis zwischen beiden Begriffen geht die Beschreibung der Definition voraus. In der ‚Definition‘, die Avicenna vorstellt, wird ein neuer Ausdruck e mittels anderer Ausdrücke <e1, …, ek>, die sich auf schon bekannte Sachverhalte beziehen, ‚erklärt‘. Die von Avicenna dann vorgenommene Erklärung, was eine ‚Definition‘ sei, hängt u.a. stark ab von dem Begriff der ‚Bekanntheit‘ und dem Begriff des ‚wahren Wesens‘. Für die Tatsache, dass ein Mensch A bestimmte Ausdrücke <e1, …, ek> einer Sprache L ‚kennt‘ oder ’nicht kennt‘, dafür gibt es keine allgemeinen Regeln oder Kriterien. Von daher macht die Verwendung der Ausdrücke ‚bekannt’/ ’nicht bekannt‘ eigentlich nur Sinn in solch einem lokalen Kontexten W* (z.B. einem Artikel, ein Buch, ein Vortrag, …), in dem entscheidbar ist, ob ein bestimmter Ausdruck e einer Sprache L schon mal vorkam oder nicht. Schwierig wird es mit dem Begriff des ‚wahren Wesens‘. In meiner Interpretation mit der dynamischen Objekthierarchie gibt es ‚das wahre Wesen‘ in Form von Objekten auf einer Stufe j, die Instanzen auf Stufen kleiner als j haben. Dazu gab es weitere Überlegungen.

7. Im folgenden Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 7 beschreibt Avicenna syntaktisch zusammengesetzte, aber semantisch einfache Ausdrücke. Innerhalb der Ausdrücke unterscheidet er die Teileausdrücke ‚Name‘, ‚Verb‘ und ‚Präposition‘. Die unterschiedliche Charakterisierung erfolgt nicht aufgrund der syntaktischen Form, sondern aufgrund der semantischen Eigenschaften, die mit diesen Ausdrücken verbunden werden. Neben dem Objektbezug, der die eigentliche Bedeutung fundiert, gibt es im Bedeutungsraum auch noch den zeitlichen und den räumlichen Aspekt. Das Zusammenspiel von Bedeutung und Ausdruck wird angerissen.

8. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 8 geht es um solche Ausdrücke E, die ‚Aussagen‘ P sind, von denen man sagt, dass sie ‚wahr‘ oder ‚falsch‘ seien. Aussagen sind eine echte Teilmenge aller Ausdrücke, $latex P \subset E$. Avicenna unterscheidet drei Arten von Aussagen: ‚kategorische‘ Aussagen, ‚Disjunktiv-konditionelle‘ und ‚Konjunktiv-konditionelle‘. Es wird ausführlich eine mögliche Wahrheitstheorie für die Zuschreibung ‚wahr’/ ‚falsch‘ diskutiert. Dann werden nochmals die Aussagetypen näher untersucht. Ein Zusammenhang mit der modernen Aussagenlogik wird hergestellt. Disjunktion, Konjunktion (und ergänzend) Implikation) sind Aussagetypen, die aus zwei Teilausdrücken A und B bestehen, die selbst wieder Aussagen sind, die wahr oder falsch sein können. Die beiden Teilausdrücke A und B werden dann durch die Teilausdrücke (oder), (und) sowie (wenn)-(dann)- verknüpft. Sie unterscheiden sich dadurch, wie der Wahrheitswert des Gesamtausdrucks von der Verteilung der Wahrheitswerte auf die Teilausdrücke festgelegt ist. Die Teilausdrücke (oder), (und) sowie (wenn)-(dann)- nennt man später dann auch ‚aussagenlogische Operatoren‘. Der Aussagetyp ‚kategorisierend‘ passt nicht in dieses Schema. Der Aussagetyp ‚kategorisierend‘ ist eine Aussage A, die wahr oder falsch sein kann unabhängig von irgendeinem aussagenlogischen Operator. Auch wird die Verneinung/ Negation diskutiert. Ausdrücke wie (Etwas)(ist nicht)(dies)(oder)(jenes) wurden rekonstruiert als $latex \neg(A)(oder)(B)$ mit dem Zeichen $latex \neg$ für ’nicht‘ oder ‚es ist nicht der Fall, dass‘.

9. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 9 kommt Avicenna auf mehrere Begriffspaare zu sprechen, die sich z.T. mit Themen berühren, die er schon vorher besprochen hat, z.T. neue Aspekte thematisieren, die nicht so ohne weiteres mit dem bisher Gesagten harmonieren. Es handelt sich z.B. um die Begriffe ‚Kategorisch‘, ‚Negation‘, ‚Universal‘, ‚Partikulär‘, die aber jetzt mit neuen Randbedingungen nochmals diskutiert werden. So stellt er die Frage, wann ‚kategorischen‘ (‚kategorisierenden‘) Aussagen ‚affirmativ‘ und wann sie ’negativ‘ sind. Ferner führt er neben den bisherigen die semantisch motivierten Begriffe ‚Name‘, ‚Verb‘ (auch ‚Term‘ genannt), sowie ‚Präposition‘ nun auch das Begriffspaar ‚Subjekt‘ und ‚Prädikat‘. Auch diese sind ’semantisch‘ motiviert, d.h. nur durch Rückgriff auf die Bedeutung kann man zur Klassifikation ‚Subjekt‘ bzw. ‚Prädikat‘ kommen. In den soeben erwähnten Kontexten wie auch in nachfolgenden Beispielen diskutiert Avicenna auch die Begriffe ‚affirmativ‘ und ’negativ‘. Zwischendrin bemerkt er auch mal, dass das Treffen einer Feststellung, eigentlich nur Sinne mache, wenn dasjenige, von dem etwas ausgesagt wird, auch existiere. Doch wird dieser Punkt nicht weiter diskutiert. Vom Subjekt einer Aussage sagt Avicenna, dass es partikulär‘ oder ‚universell‘ sein kann. Falls universell, dann kann man unterscheiden, ob sie ‚unbestimmt‘ (engl.: ‚indeterminate‘) ist – wie viele genau involviert sind — oder eben ‚bestimmt‘ (engl.: ‚determinate‘). Ferner illustriert er am Beispiel der kategorisierenden Aussagen auch die Begriffe ’notwendig‘ und ‚kontingent‘. Diese Verwendung der Begriffe stimmt überein mit den zuvor eingeführten Begriffe ‚wesentlich‘ und ‚akzidentell‘. Auch erwähnt Avicenna den Begriff ‚möglich‘. Er sieht mindestens zwei Verwendungsweisen von ‚möglich‘: In der Diskussion dieses Abschnitts werden einerseits einige Widersprüchlichkeiten in den Ausführungen Avicennas sichtbar gemacht, andererseits wird die Rekonstruktion einer möglichen systematischen Theorie zur Logik Avicennas fortgesetzt. Die wichtigsten Kritikpunkte kreisen um das Begriffspaar ‚affirmativ – negativ‘ mit der Kritik, dass beide Begriffe auf unterschiedlichen semantischen Ebenen liegen. Ferner widerspricht die Handhabung der Quantoren durch Avicenna der allgemeinen Verwendung.

10. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 10 diskutiert Avicenna seine Begriffe ‚Konjunktives‘ und ‚Disjunktives Konditional‘ unter verschiedensten Aspekten. Einige davon sind die Quantoren (wobei er auch Quantoren über die Zeit benutzt!), das Begriffspaar ‚Antezedenz – Konsequenz‘, der Begriff der ‚Harmonie‘, und wiederholt die Aspekte ‚Existenz‘, ‚Affirmation‘ sowie ‚Bestimmt/ Unbestimmt‘. Alle diese Aspekte werden in diesem Blogeintrag schon ein wenig ‚vorsortiert‘, um dann im nachfolgenden Blogeintrag weiter rekonstruierend diskutiert zu werden.

11. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 11 erfolgt eine ‚rekonstruierende Diskussion‘ von Avicennas Überlegungen aus Blogeintrag 10. Seine Überlegungen werden aufgegriffen und in einen theoretischen Rahmen eingeordnet, der es erlaubt, die Begriffe schärfer zu fassen und sie dadurch besser voneinander abzugrenzen. Nach einer Übersicht über die Struktur der Aussagen erfolgt dann eine Rekonstruktion von Bedeutungszuordnungen und eine Erklärung von Begriffen wie ‚wahr’/ ‚falsch‘, ‚Existenz‘, und ‚möglich‘.

12. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 12 diskutiert Avicenna den Fall widersprüchlicher Aussagen. Gemessen an dem bisher Gesagten bringt er in diesem Abschnitt keine neuen Aspekte ins Spiel. Wohl aber bietet dieser Abschnitt weitere Beispiele für sein Auffassung des Sachverhalts. Sie belegen, wie schwer er sich durchgängig damit tut, in dem unscharfen Wechselspiel von Ausdrucksseite und Bedeutungsseite eine konstante Verwendungsweise seiner Begriffe durchzuhalten. In diesem Blogeintrag erfolgt die Diskussion seines Textes immer unmittelbar hinter jedem Punkt in Form einer Anmerkung.

13. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 13 diskutiert Avicenna die Möglichkeit der Konvertierung von Aussagen mit Quantoren in solche, deren Bedeutung trotz Veränderung von Ausdruckselementen ‚erhalten‘ bleibt. In einigen Beispielen widerspricht er sich selbst; manche Stellen sind unklar. Es zeigt sich allgemein: (i) die Formulierung von Konvertierungsregeln greift beständig auf bestimmte unterstellte Bedeutungen zurück und (ii) genau diese unterstellten Bedeutungen werden nicht hinreichend klar definiert. Daraus entsteht die Forderung, diese unterstellte Bedeutung klar zu definieren und auf dieser Basis alle logischen Ausdruckselemente eindeutig zu definieren (was im nachfolgenden Abschnitt dann unternommen wird).

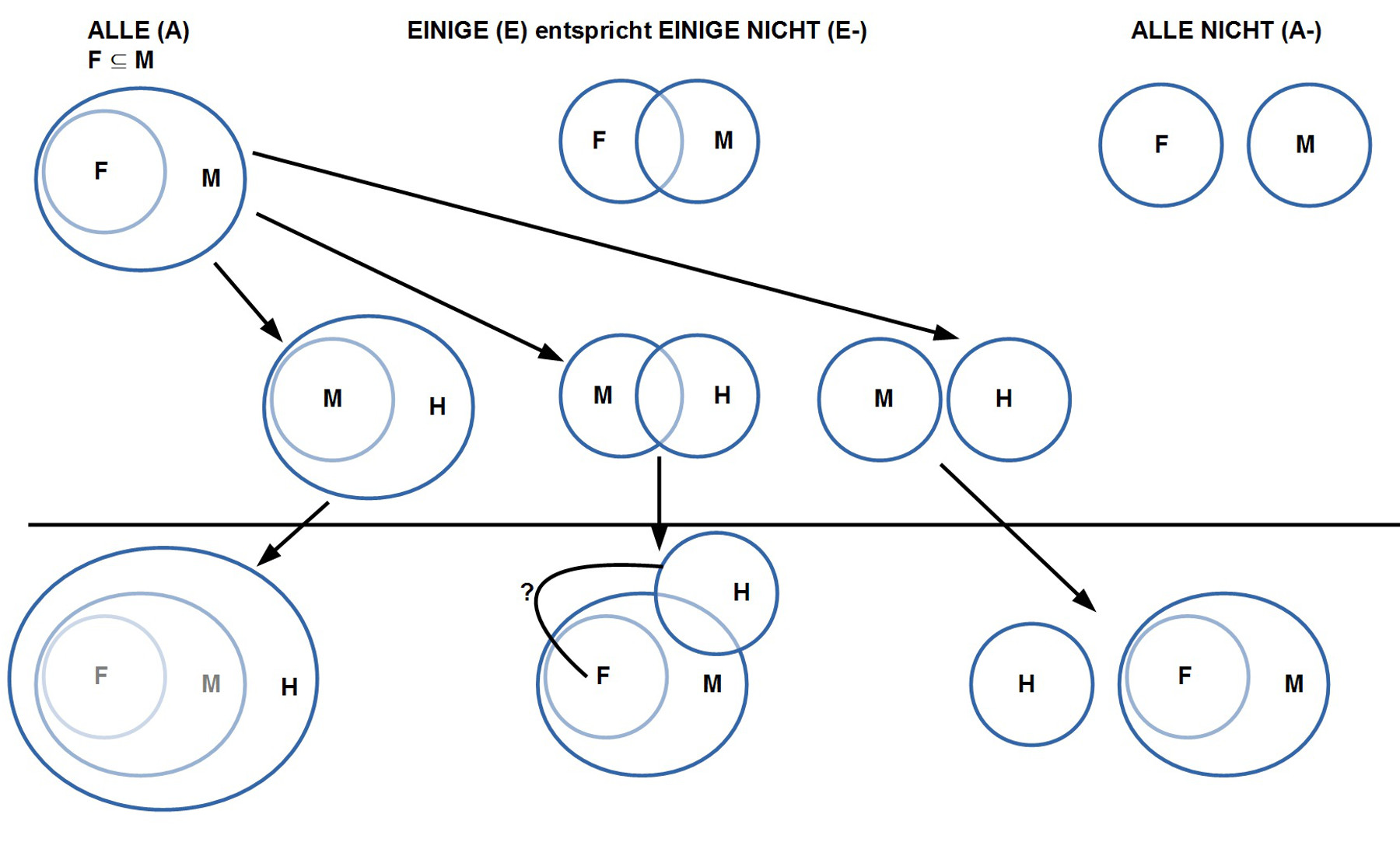
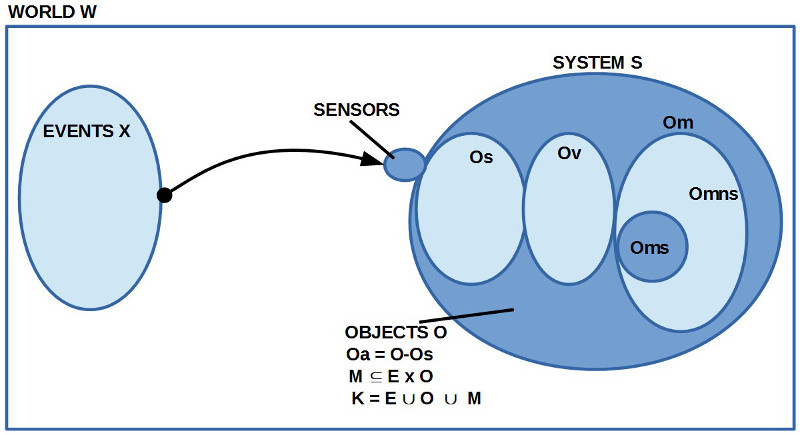
14/14b. In den Blogeinträgen AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 14 sowie AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 14b geht es darum, erstmalig einen theoretischen Rahmen für eine Semantik zu formulieren, mit der man die Logik Avicennas konsistent entwickeln kann. Abschnitt 14b stellt eine Überarbeitung des Eingangsteils von Abschnitt 14 dar. Es hat sich gezeigt, dass die in 14b gewählte Begrifflichkeit für das weitere Vorgehen ‚günstiger‘ wirkt. Aber wir befinden uns noch in der Phase der ‚Annäherung‘ an das ‚Neue‘.

15. In dem Blogeintrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 15 geht es um die Feinstruktur von Aussagen. Avicenna unterteilt ja Ausdrücke anhand inhaltlicher Kriterien nach Subjekt S, Prädikat P und ergänzend nach Quantoren Q. Es fragt sich, wie man diesen Ausdrucksteilen eine ‚Bedeutung‘ im Objektraum O zuordnen kann. Wichtig ist hier die schon früher getroffene Unterscheidung zwischen ‚echten‘ und ‚unechten‘ Objekten. ‚Unechte‘ Objekte wurden als ‚Eigenschaften‘ bezeichnet. Mit dieser Terminologie kann man sagen, dass die Objekthierarchie O primär von echten Objekten gebildet wird; unechte Objekte als Eigenschaften treten nur im Kontext eines echten Objekts auf. Damit kann man die begriffe ‚Gattung‘ und ‚Art‘ einführen. Gattungen, die keine Gattungen mehr ‚über sich‘ haben können, sollen hier ‚Kategorien‘ genannt werden. Setz man Definitionen von Worten voraus, dann kann man ach erklären, warum eine Aussage wie ‚a ist eine Tasse‘ ‚rein definitorisch‘ (bzw. ‚rein analytisch‘) ‚wahr ist, unabhängig davon, ob diesem gedanklichen Sachverhalt etwas Sinnliches entspricht. Im Gegensatz zu solch einer rein definitorischen (analytischen) Wahrheit eines Objekts a soll hier die ursprünglich vereinbarte ‚Wahrheit‘ durch Bezug auf eine ’sinnliche Gegebenheit‘ $latex s \subseteq Os$ ‚ontologische‘ Wahrheit genannt werden. Solange wir uns in unseren Aussagen auf das Enthaltensein eines Objektes a in einem Gattungsobjekts X beschränken ‚a ist ein X‘ oder das Feststellen von Eigenschaften der Art ‚a hat b‘ kann man sagen, dass eine Aussagestruktur wie (S P) wie folgt interpretiert werden kann: Es gibt einen Ausdruck A=(AsAp), bei dem ein Ausdrucksteil As sich auf ein echtes Objekt M(As) = $latex a \in Oa$ bezieht und der andere Ausdrucksteil Ap bezieht sich auf die Beziehung zwischen dem Objekt a und entweder einem Gattungsobjekt X (Ap = ‚ist ein X‘) oder auf eine Eigenschaft Y (Ap = ‚hat Y‘). Hierbei ist eine gewisse ‚Asymmetrie‘ zu beachten. Die Bedeutung vom Ausdrucksteil As – M(As) – bezieht sich auf eine ‚konkrete‘ Eigenschaftsstruktur innerhalb der Objekthierarchie. Die Bedeutung vom Ausdrucksteil Ap – M(Ap) – bezieht sich auf eine ‚Beziehung‘ / ‚Relation’/ ein ‚Verhältnis‘ [R] zwischen dem bezeichneten Bedeutungsobjekt M(As) = a und einem anderen bezeichneten Bedeutungsobjekt M(Ap), also R(M(As), M(Ap)). Die Beziehung R ist selbst kein ‚Objekt‘ so wie das Objekt a oder das implizit angenommene ‚Bezugsobjekt‘ X bzw. Y von a. Eine solche Beziehung R setzt – um prozessural ‚hantierbar‘ zu sein – eine zusätzliche ‚Objektebene‘ voraus, auf der es ein R-Objekt gibt, das die Beziehung zwischen dem a-Objekt und dem X-Y-Objekt ‚repräsentiert.

16. In dem Blogeintrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 16 wird die Analyse der vorausgesetzten Objekthierarchie O und der damit interagierenden Ausdrucksstruktur E weiter analysiert. Nach der Analyse der Feinstruktur von (S P) werden die Aspekte Anzahl, Raum und Zeit betrachtet. Es wird gezeigt, wie man für diese Aspekte sowohl ‚globale Quantoren‘ wie auch ‚lokale Relationen‘ einführen kann; zudem ist die Wechselwirkung zwischen diesen Aspekten konfliktfrei, da sie voneinander unabhängig sind.

17. In dem Blogeintrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 17 geht es um die Frage, wie man Aussagen über Veränderungen in der hypothetisch angenmmenen Bedeutungsstruktur nachzeichnen kann. Es lässt sich erkennen, dass die Kodierung von Veränderungen mittels Ausdruckselementen innerhalb eines Prädikates P mittels ‚Veränderungsausdrücken‘ V (‚Verben‘) oft nicht nur die beteiligten Objekte Y benennt, sondern zusätzlich zahlreiche weitere Ausdruckselemente aktiviert, die räumliche Gegebenheiten R_r bezeichnen, zeitliche Relationen R_t, zusätzliche Eigenschaften At an den Veränderungen; dazu ferner spezielle kulturelle Relationen R_x einbeziehen können sowie mit zusätzlichen Subjektrepräsentationen operieren. Auch kann man beobachten, wie die Aneinanderreihung von unterschiedlichen Sachverhalten (S P) mit logischen Operatoren (S P) UND (S2 P2) auch zu speziellen Verkürzungen führen kann wie (S P1 UND P2). Dies lässt erahnen, dass eine vollständige Analyse auch nur einer einzigen Alltagssprache von ihrer logisch relevanten Semantik her eine schier unendliche Aufgabe ist. Diese wird weder ein einzelner Mensch alleine noch viele Menschen über viele Genrationen hinweg jemals vollständig erfüllen können. Was aber möglich erscheint, das ist die Analyse des grundlegenden Mechanismus, der sich mit Hilfe von evolvierenden Computermodellen experimentell untersuchen und mit realen semiotischen Systemen überprüfen lässt.

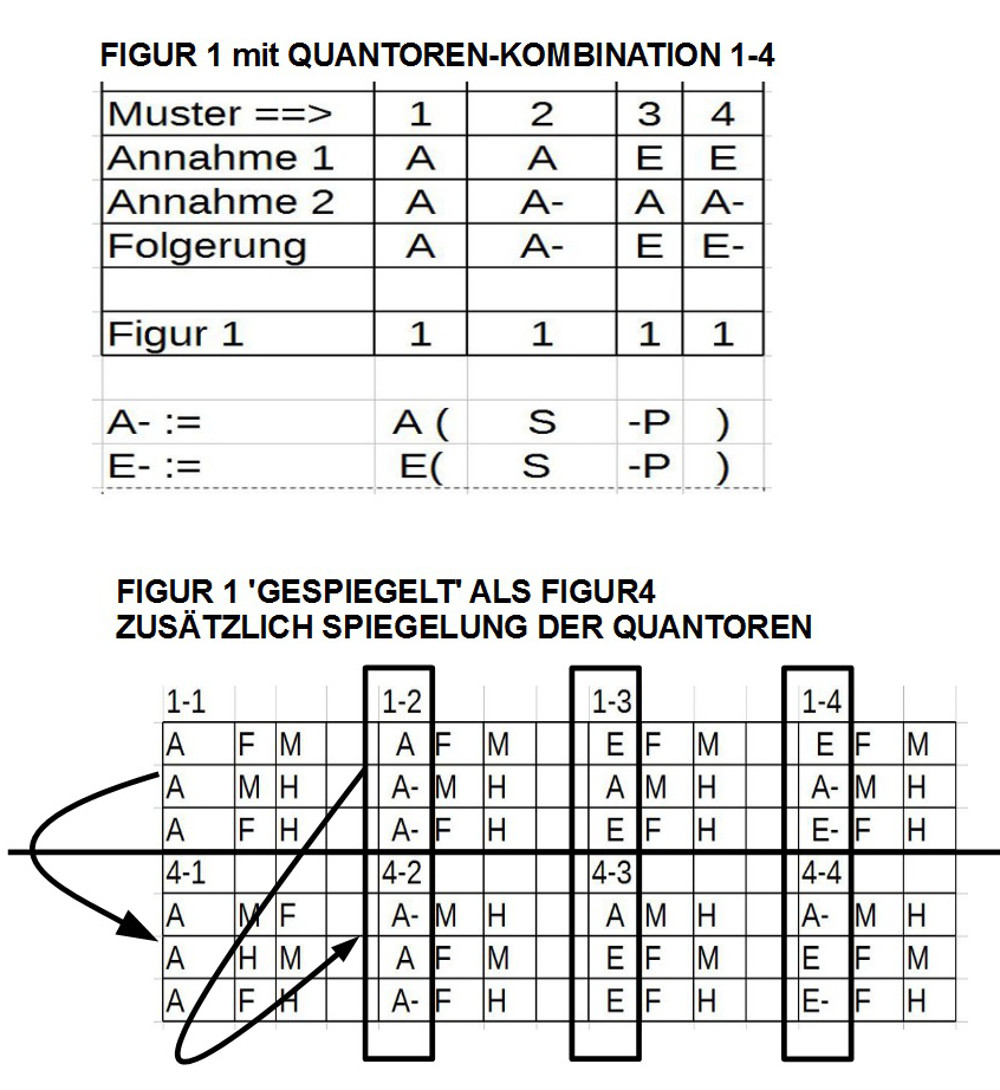
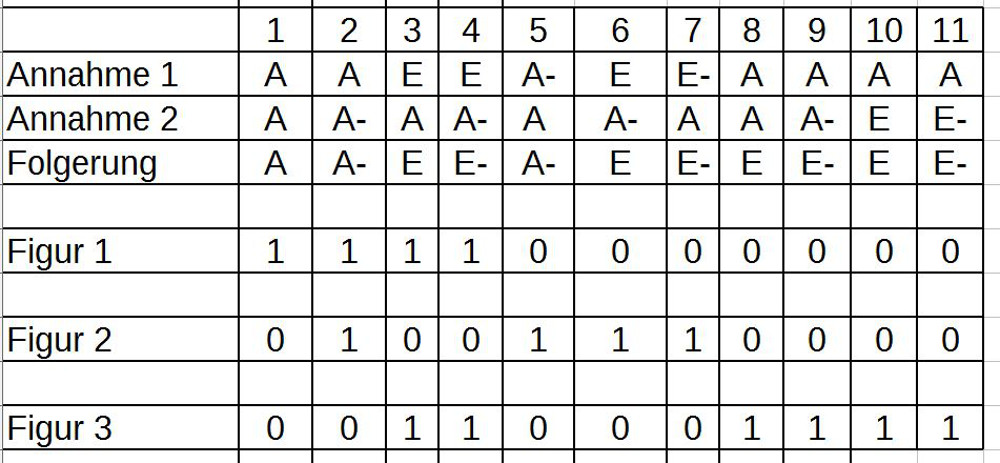
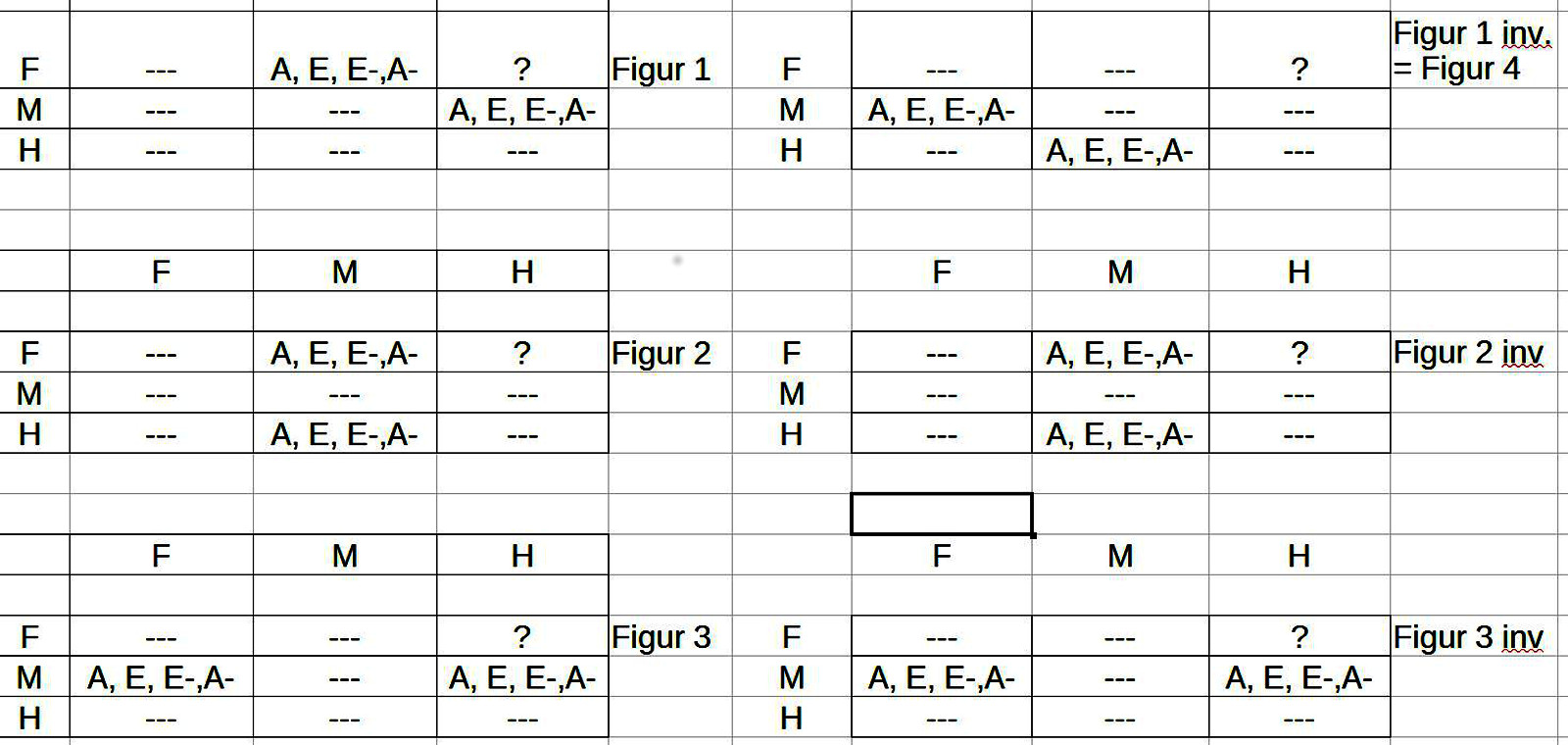
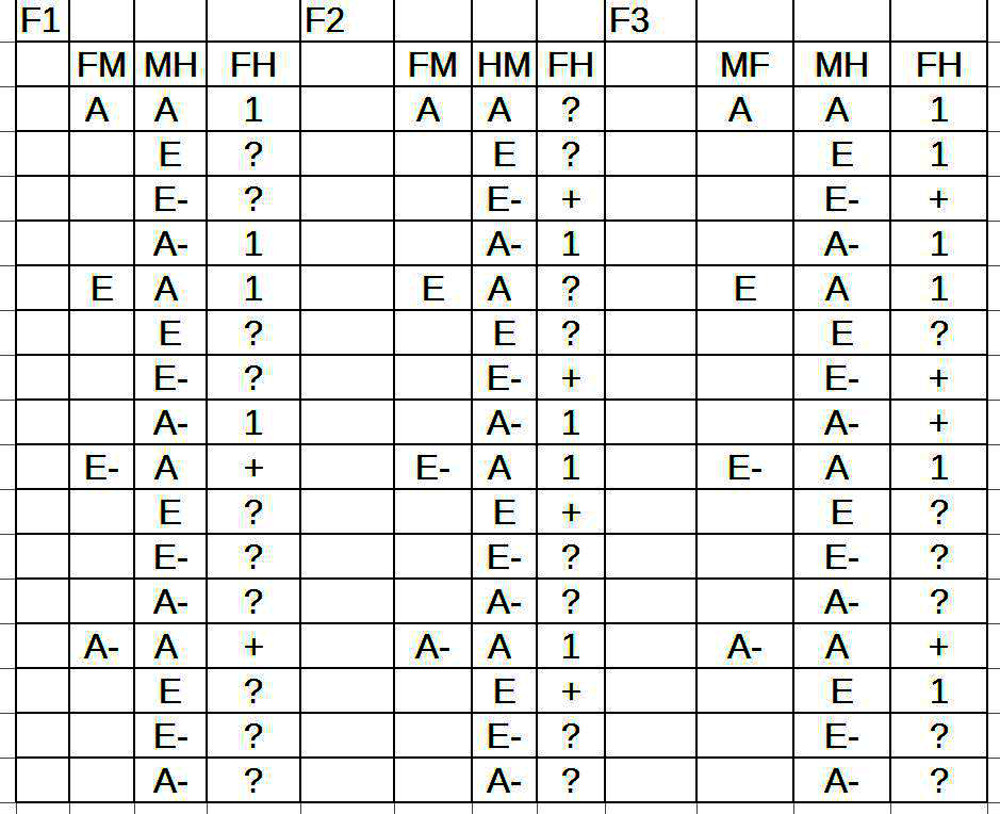
18. In dem Blogeintrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 18 weitet sich nun der Blick Avicennas auf das Wissen allgemein, und konzentriert sich im Wissen auf das schlussfolgernde Denken in Form von ‚beweisenden Syllogismen‘. Nach einer Definition von ‚Syllogismus‘ unterscheidet er dann zwei Arten von Syllogismen ‚Konjunktiver‘ Syllogismen und ‚Disjunktiver‘ Syllogismus. Am Beispiel des ‚Konjunktiven Syllogismus‘ führt Avicenna dann eine Reihe von technischen Begriffen ein. Dann stellt Avicenna zusätzliche Beschränkungen vor, um die 256 möglichen Figuren/ Muster auf nur 27 mögliche Muster einzuschränken. Alle seine Festlegungen geschehen ohne eigentliche Begründung.

19. In dem Blogeintrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 19 beginnt die Diskussion um die Interpretation der syllogistischen Schlussfiguren am Beispiel der ersten Figur (A F B), (A B H) und (A F H) mit der Quantorenbelegung ‚AAA‘. In einzelnen Schritten wird dann eine erste Skizze zu einer Logik auf der Basis einer dynamischen Objektstruktur erarbeitet. Zentrale Begriffe sind hier OBJEKTIFIZIERUNG, ENTHALTENSEIN, ZUSCHREIBUNG und VERERBUNG. In dieser Skizze werden auch ‚Aktivitäten‘ berücksichtigt, die in dem Muster zur ersten Figur nicht vorkommen, zusätzlich werden neben den Anzahlquantoren auch Raum- und Zeitquantoren berücksichtigt.

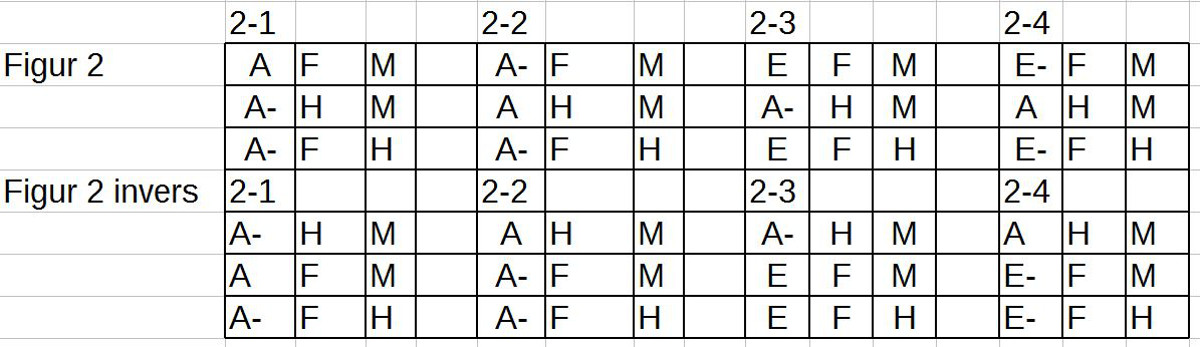
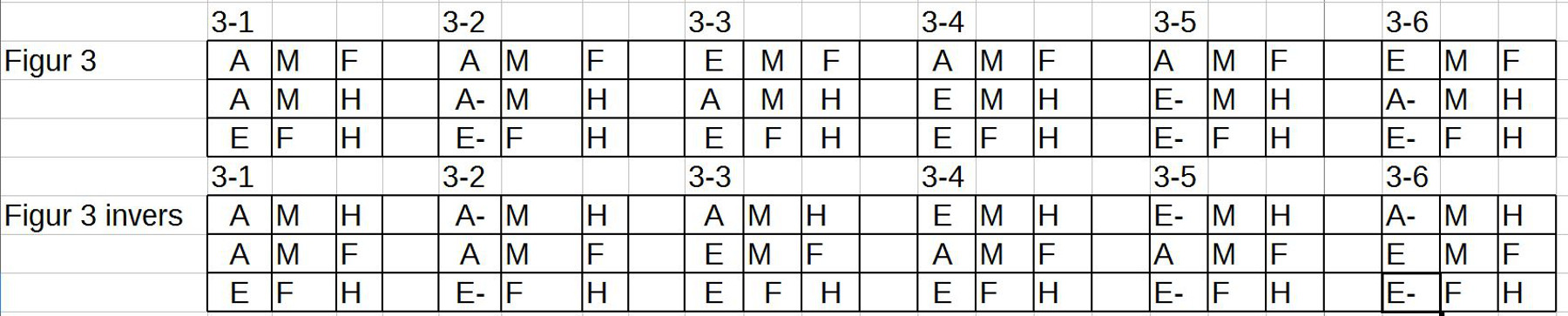
20. In dem Blogeintrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 20 geht es um die Interpretation des zweiten Musters der ersten syllogistischen Schlussfigur ‚A F ist B‘, ‚A B ist nicht H‘ (als ‚Kein A ist B‘), ‚A F ist nicht H‘ (als ‚Kein F ist H‘), dazu die Beispiele ‚Jeder ausgedehnte Körper ist farbig‘, ‚Kein farbiger Körper ist unerschaffen‘, ‚Kein ausgedehnter Körper ist unerschaffen‘. Wir treffen in diesem Muster wieder auf den Prozess der Objektifizierung, tatsächlich sogar in impliziten Formen mit der expliziten Angabe von Eigenschaften und der stillschweigenden Annahme einer daraus sich ergebenden Mengenbildung. Zusätzlich finden sich wieder Enthaltensbeziehungen einerseits anhand von Eigenschaftszuschreibungen, andererseits durch Benutzung von Anzahlquantoren. Die Zuschreibung von Eigenschaften wird explizit vorgenommen. Eine Vererbung von Eigenschaften von einer Menge zur anderen tritt nur implizit über eine Enthaltensbeziehung auf. Es tritt nur eine Sorte von Quantoren auf. Auch sei angemerkt, dass außer der Negation kein weiterer aussagenlogischer Operator auftritt.

21. In dem Blogeintrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 21 geht es um die Interpretation der Muster 3-4 der Schlussfigur 1. Dabei entsteht die Vermutung, dass viele der Unterscheidungen von Avicenna (die weitgehend auf Aristoteles zurückgehen!) möglicherweise ‚redundant‘ sind, d.h. mit anderen Formulierungen letztlich doch ‚das Gleiche‘ sagen. Der Ansatzpunkt für diese Vermutung liegt darin begründet, dass die Unterscheidung von einem Term als ‚Subjekt‘ (S) und als ‚Prädikat‘ (P) auf Seiten der abstrakten Bedeutungsstruktur als Bedeutungsrepräsentation jeweils ein ‚echtes‘ oder ein ‚unechtes‘ Objekt haben können, und zwar so, dass diese Strukturen ‚fließend‘ sind: jedes ‚echte‘ Objekt kann als ‚unechtes‘ interpretiert werden und umgekehrt. Weitere Vereinfachungen deuten sich an. Diese sollen im Folgenden überprüft werden.

Fortsetzung folgt …

QUELLEN

• Avicenna, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
• Digital Averroes Research Environment
• Immanuel Kant, Critik der reinen Vernunft‘, Riga, 1781
• Konrad Lorenz, 1973, ‚Die Rückseite des Spiegels. Versuch einer Naturgeschichte des menschlichen Erkennens‘, München, Zürich: Piper
• Günther Patzig, ‚Die Aristotelische Syllogistik‘, 3,verb.Aufl., Göttingen: Vandenhoeck & Rupprecht, 1969
• Nicholas Rescher (1928 – ),The Development of Arabic Logic. University of Pittsburgh Press, 1964
• Hans-Jörg Sandkühler (Hg.) unter Mitwirkung von Dagmar Borchers, Arnim Regenbogen, Volker Schürmann und Pirmin Stekeler-Weithofer, ‚Enzyklopädie Philosophie‘, 3 Bd., Hamburg: FELIX MEINER VERLAG, 2010 (mit CD-ROM)
• Stanford Encyclopedia of Philosophy, Aristotle’s Logic
• Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
• Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
• Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
• Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7

Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER.