Archiv der Kategorie: Bedeutung eines Wortes

GEMEINSAMKEIT IN DER VIELFALT – GRASWURZEL-/ BOTTOM-UP-PHILOSOPHIE – Memo zur philosophieWerkstatt vom 12.Okt.2014

Ähnliches, Allgemein, Alltag, Alltagssprache, Analytisch, Apriori, Bedeutung, Bedeutung - abstraktes Konstrukt, Bedeutung eines Wortes, Bedeutungsbeziehung, Bedeutungskorrelat, Bedeutungsmaterial, Bedeutungsraum, Begriffe, Bewußtsein, Bibel, Bild im Kopf, Biologische Evolution, Philosophiewerkstatt, Semantik, Sozialer Druck, Sprache, Sprache und Denken, Sprachliche Äußerung, Sprachmaterial, Übertragung, Vorurteil, Vorwissen, Wahr, Wahrheit, Wahrheit - definitorische (analytische), Wahrheit - Frage nach, Wahrheit - ontologische, Wahrheitskriterium, Wahrnehmen, Wahrscheinlichkeit

Dieses Memo bezieht sich auf die philosophieWerkstatt v.2.0 vom 12.Okt.2014.

1. Ein neuer Ort, eine neue Zeit, neue Menschen …. die philosophieWerkstatt v2.0 ging an den Start und trotz schönem Wetter und vielen Grippeinfizierten gab es eine bunte Runde von Gesprächsteilnehmern die sich zu einem philosophischen Gespräch zusammen fanden.

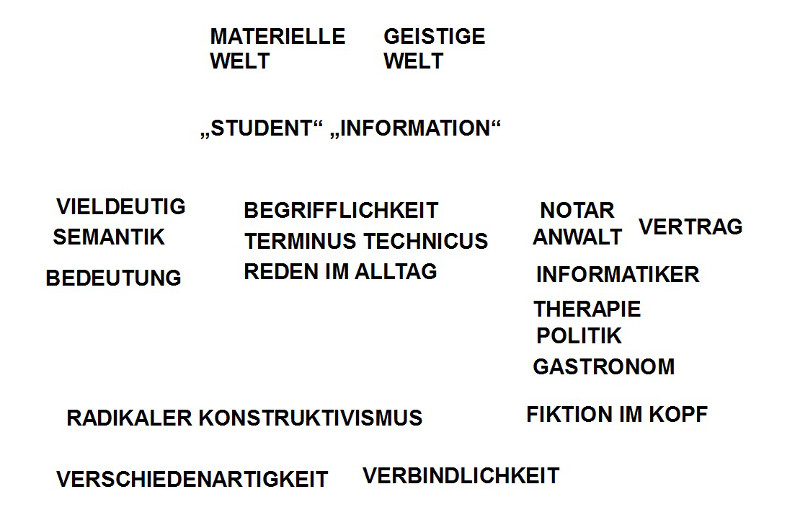
2. In einer kleinen ‚Aufwärmphase‘ konnte jeder etwas von sich und seinen Erwartungen erzählen und es wurde ein erstes Begriffsfeld sichtbar, das von Vielfalt kündete und einen erkennbaren Zusammenhang noch vermissen lies (siehe nachfolgendes Bild).

Begriffe im Raum, unverbunden, der Anfang
Begriffe im Raum, unverbunden, der Anfang

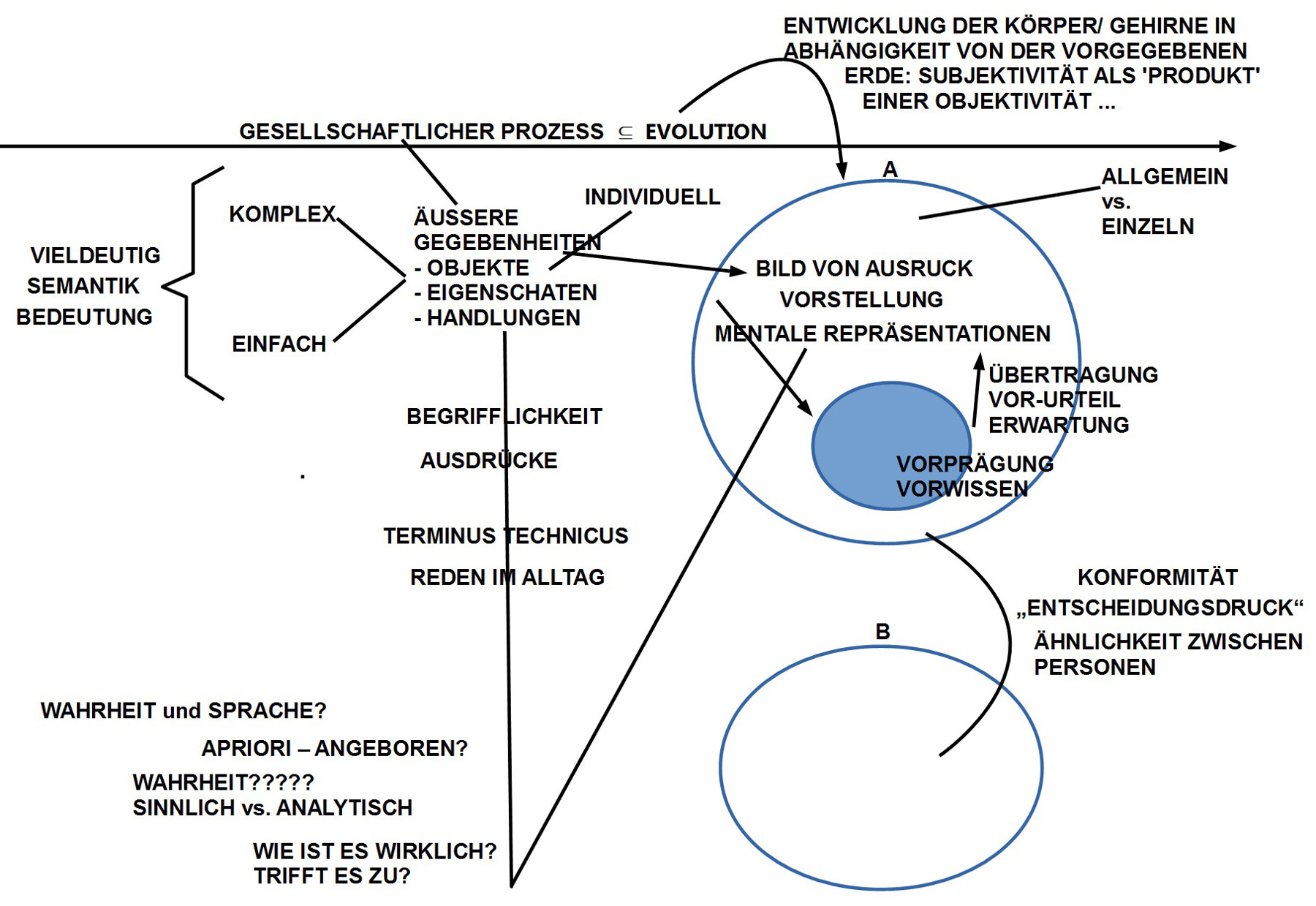
3. Es stand die Frage im Raum, ob und wie man hier zu einem verbindlichen Zusammenhang kommen könne? Wie – hier vorgreifend auf das Ergebnis des Gespräches – das abschließende Gesprächsbild andeutet, kam es zu immer mehr Differenzierungen, wechselseitigen Abhängigkeiten, Verdichtungen und Abstraktionen, die – wenngleich noch zaghaft – eine erste Struktur andeuten, an der man bei einem Nachfolgegespräch weiter anknüpfen könnte.

Begriffe in einem beginnenden Zusammenhang, Umrisse einer Struktur
Begriffe in einem beginnenden Zusammenhang, Umrisse einer Struktur

BILDER VON DER WELT – BEDEUTUNG

4. Eine erste Wendung im Gespräch kam durch den Hinweis, dass die ‚Bedeutung‘, die wir von den ‚Ausdrücken‘ einer Sprache unterscheiden, ‚in unserem Kopf‘ zu verorten sei. Dort. ‚in unserem Kopf‘ haben wir ‚Bilder von der Welt‘ (‚Vorstellungen‘, ‚mentale Repräsentationen‘), die für uns ‚Eigenschaften der umgebenden Welt‘ repräsentieren.

VORWISSEN

5. Bald kam auch der Begriff des ‚Vorwissens‘, der ‚bisherigen Erfahrung‘, einer ‚Vorprägung‘ ins Spiel: gemeint war damit, dass wir in jedem Augenblick nicht vom Punkt Null beginnen, sondern schon Erfahrungen in der Vergangenheit gemacht haben, die auf die aktuelle ‚Wahrnehmung der Welt‘ einwirken: als ‚Erwartungen‘, als ‚Vor-Urteil‘, als ‚Übertragung‘.

SOZIALER DRUCK

6. Hier wurde auch darauf hingewiesen, dass die ‚Interpretation der Wahrnehmung‘ von anderen Menschen (‚Gruppenzwang‘, ‚gesellschaftliche Gewohnheiten/ Erwartungen‘, ‚Prüfungssituationen‘) zusätzlich beeinflusst werden kann. Während man normalerweise spontan (fast unbewusst) entscheidet, wie man eine Wahrnehmung interpretieren soll (obgleich sie vieldeutig sein kann), kann dieser Prozess unter sozialem Druck gestört werden; wie zögern, werden unsicher, bemerken, dass die Situation vielleicht nicht eindeutig ist, und suchen dann nach Anhaltspunkten, z.B. nach den Meinungen der anderen. Oft ist es so, dass die ‚Mehrheit‘ besser ist als die Meinung eines einzelnen; die Mehrheit kann aber auch völlig daneben liegen (berühmtes Galileo-Beispiel).

ÄHNLICHKEITEN ZWISCHEN PERSONEN

7. Die Frage war, wie es denn überhaupt zu ‚Ähnlichkeiten‘ zwischen Personen kommen kann, wenn jeder seine Bilder im Kopf hat?

8. Ein Schlüssel scheint darin zu liegen, dass jeder seine Bilder in seinem Kopf anlässlich der Gegebenheiten der umgebenden Welt ‚formt‘. Sofern die umgebende Welt für alle die ‚gleiche‘ ist, lässt sich von daher eine gewisse Ähnlichkeit der Bilder motivieren.

9. Zusätzlich gibt es aber auch die Sachlage, dass die Körper der Menschen mit ihren Organen und Prozessen, insbesondere mit ihrem Gehirn und den darauf basierenden Information verarbeitenden Prozessen, eine gewisse Ähnlichkeit zwischen allen Menschen aufweisen, so dass auch dadurch Ähnlichkeiten zwischen den Bildern im Kopf begünstigt werden.

BEGRENZUNG DES BEWUSSTSEINS

10. In der neuzeitlichen Orientierung am Bewusstsein als primärer Erkenntnisquelle (ungefähr seit Descartes und später bis zur Phänomenologie) gab es keine Ansatzpunkte, um diese implizite ‚Harmonie der Körper und Erkenntnisse‘ aufzuhellen. Die antike Philosophie – insbesondere Aristoteles und seine Schüler – hatte zwar Ansatzpunkte, die Erkenntnisse über die Welt einzubeziehen, aber die damaligen ‚Welterkenntnisse‘ reichten nicht aus, um das moderne empirische Wissen über die physikalische, chemische, biologische und kulturelle Evolution vorweg zu nehmen. Erst mit den neuen Wissenschaften und einer davon inspirierten Strömung einer ‚evolutionär inspirierten‘ Erkenntnistheorie und Philosophie lieferte erste sachdienliche Hinweise, dass die unübersehbare ‚Harmonie der Körper‘ auch ein Grund für die Ähnlichkeit zwischen den Bildern in den verschiedenen Köpfen sein kann.

SCHLÜSSEL EVOLUTION

11. Mehr noch, die verblüffende ‚Passung‘ von menschlicher Erkenntnis zur ‚umgebenden Welt‘ ist letztlich vollständig induziert von einer evolutionären Entwicklung, in der sich nur solche Organismen ‚durchsetzen‘ konnten, die relativ am besten die ‚lebensfördernden Eigenschaften‘ der umgebenden (aber auch in sich sich verändernden) Welt aufgreifen und nutzen konnten.

12. Wenn man davon sprechen kann, dass der Menschen ein ‚Ebenbild‘ sei, wie es biblische Texte nahelegen (hier ohne kritischen Kommentar), dann zunächst mal ein Ebenbild der vorgegebenen Erde als Teil eines Sonnensystems als Teil einer Galaxie als Teil eines BigBang-Universums (Weiterreichende Interpretationen sind damit per se noch nicht ausgeschlossen).

BILDER IM KOPF vs. WELT

13. Es wurde auch festgestellt, dass man zwischen den ‚Bildern von der Welt im Kopf‘ und den ’sprachlichen Ausdrücken‘ unterscheiden muss.

ALLGEMEINBEGRIFFE

14. Die ‚Bilder von der Welt‘ repräsentieren irgendwie (mal mehr, mal weniger ‚passend‘) die ‚Gegebenheiten‘ der umgebenden Welt. Dies geschieht durch eine ‚denkerische‘ Mixtur aus ’sinnlicher Erfahrung von Einzelnem‘ und ‚denkerischer Abstraktion von Allgemeinheiten‘, so dass wir in jedem Moment zwar einen einzelnen konkreten Gegenstand identifizieren können, zugleich aber auch immer einen ‚allgemeinen Begriff‘, eine ‚Kategorie‘ zur Verfügung haben, die anhand von ‚abstrahierten Eigenschaften‘ einzelne Gegenstände als ‚Beispiele‘ (‚Instanzen‘) einer allgemeinen Struktur erscheinen lässt. Unser Denken lässt gar nichts anderes zu; es ‚zwingt‘ uns zur ‚automatischen‘ (‚unbewussten‘) Konstruktion von ‚Allgemeinbegriffen‘.

SPRACHE UND DING

15. Es wurde darauf hingewiesen, dass wir ja auch verschiedene Sprachen sprechen und dass möglicherweise die ‚Bilder im Kopf‘ bis zu einem gewissen Grade unabhängig von der verwendeten Sprache sind. Deswegen können wir auch zwischen den Sprachen übersetzen! Weil die körpergebundenen Sachstrukturen – bis zu einem gewissen Grade – sprachunabhängig gegeben sind und sich ‚aufbauen‘, können die Ausdrücke einer Sprache L darauf Bezug nehmen und durch andere ‚bedeutungsgleiche‘ Ausdrücke ‚ersetzt werden.

VERÄNDERLICHE WELT vs. STATISCHE BILDER

16. Die ‚Bedeutung‘ sprachlicher Ausdrücke (ihre ‚Semantik‘) begründet sich also von den körperbedingten Objektstrukturen her. Wenn nun die umgebende Welt sich ändert (Prozess, Geschichte, Evolution, …), dann ändern sich zwar die Sachstrukturen in der Welt, nicht aber unbedingt synchron die Bilder im Kopf eines Menschen. Damit entsteht das, was wir oft erleben: Menschen benutzen Ausdrücke einer Sprache L, ‚Begriffe‘, ‚Termini‘, die sie mit bestimmten ‚Bildern im Kopf‘ verknüpfen (assoziieren), aber diese Bilder können ‚veraltet‘ sein, da sich die Gegebenheiten in der Welt mittlerweile verändert haben (im Gespräch wurde der Ausdruckswandel des Begriffs ‚Student‘ angesprochen).

EINFACH vs. KOMPLEX

17. Vor dem Hintergrund einer ‚erlernten‘ Bedeutung kann es dann passieren, dass die ‚erlernten‘ Bedeutungen aus einer früheren Zeit die Welt ‚einfacher‘ erscheinen lassen als die gegenwärtige Welt mit ihrer wachsenden Vielfalt (es standen die Bemerkungen im Raum, dass Mädchen und junge Frauen es früher ‚einfacher‘ gehabt haben sollen als Mädchen und junge Frauen heute).

WAS IST WAHRHEIT?

18. An diesem Punkt im Gespräch angekommen stellte sich nochmals die Frage nach der ‚Wahrheit‘, ein Begriff, der ganz am Anfang etwas isoliert im Raum stand.

19. Ausgangspunkt ist die alltägliche Beobachtung, dass wir manchen Aussagen als ‚richtig‘, manche als ‚falsch‘ bezeichnen. Dies knüpft an dem Umstand an, dass ‚Behauptungen über die Gegebenheiten der Welt‘ bis zu einem gewissen Grade ‚überprüfbar‘ sind. D.h. es scheint, dass wir die ‚Bilder in unserem Kopf‘ mit den sinnlich wahrnehmbaren Gegebenheiten der umgebenden Welt bis zu einem gewissen Grad so ‚vergleichen‘ können, dass wir eine ‚Übereinstimmung‘ oder ‚Nicht-Übereinstimmung‘ feststellen können, und zwar alle Menschen in gleicher Weise.

20. Wenn wir diesen grundsätzlichen Sachverhalt zum Ausgangspunkt nehmen, dann würde der Begriff ‚Wahrheit‘ in diesem Kontext bedeuten, dass eine Aussage mit ’sinnlicher Bestätigung‘ sowohl ‚richtig‘ als auch ‚wahr‘ wäre bzw. — falls keine Übereinstimmung vorliegt –, ’nicht richtig‘ bzw. ‚falsch‘ bzw. ’nicht wahr‘ wäre.

21. Bei diesem Interpretationsansatz werden damit die ‚Gegebenheiten der Welt‘ zum Ausgangspunkt, zur ‚Vorgabe‘, zum ‚Maßstab‘, an dem wir uns letztlich orientieren. Davon abgeleitet könnte man dann auch – ganz im Sinne der antiken Metaphysik und Ontologie – davon sprechen, dass ‚das Seiende‘, wie es uns – in gewissem Sinne ‚a priori‘ – vorgegeben ist, das ‚Wahre‘, die ‚Wahrheit‘ verkörpert, an der wir uns orientieren müssen, wollen wir im Sinn der Welt/ des Sonnensystems/ der Galaxie/ des BigBang-Universums/ des … ‚wahr‘ sein. Empirische Wissenschaft ist dann nichts anderes als antike Metaphysik (dafür gäbe es noch mehr Argumente).

22. Eine solcherart (ontologisch) verstandene Wahrheit ist dann nicht beliebig, sondern eher ‚verpflichtend‘: wer das ‚Leben‘ ‚achtet‘ und ‚liebt‘ muss sich eigentlich an dieser Wahrheit orientieren. Dies wäre damit auch die mögliche Begründung einer ‚Ethik des Lebens‘, die sich z.B. als ‚ökologisches Denken‘ manifestiert.

ANALYTISCH WAHRHEIT

23. Wenn wir annehmen, dass wir zu einem bestimmten Zeitpunkt ‚Bilder im Kopf‘ von der umgebenden Welt haben und wir diese Bilder als ‚zutreffen‘ – sprich als ‚wahr‘ – betrachten, dann können wir oft auch auf der Basis dieser vorausgesetzten Bilder ‚Schlüsse ziehen‘. Berühmt sind die Beispiele mit Syllogismen wie (Annahme 1) ‚Alle Menschen sind sterblich‘, (Annahme2:) ‚Sokrates ist ein Mensch‘, (Schluß:) ‚Sokrates ist sterblich‘. Nimmt man an, dass Annahme 1 und 2 ‚wahr‘ sind, dann folgt ‚analytisch‘ (ohne Bezug auf die aktuelle empirische Welt), der Schluss. Die Wissenschaft der Logik arbeitet im Prinzip nur mit solchen analytischen Schlüssen und ihren möglichen (formalen) Formen. Sie weiß als Wissenschaft der Logik nichts von der Welt (was sich auch darin auswirkt/ auswirken kann, dass sie formale Strukturen entwickelt, die mehr oder weniger ‚unbrauchbar‘ für das weltbezogene Alltagsdenken sind).

ALLE SIND TRÄGER DER WAHRHEIT

24. Rückblickend zu diesem Gespräch kann man also sagen, dass letztlich jeder Stücke der allgemeinen Wahrheit mit sich herum trägt und dass es eigentlich nur darauf ankommt, diese einzelnen Fragmente zusammen zu sammeln und sie in rechter Weise ‚zusammen zu fügen’… Graswurzel-Philosophie … Bottom-Up Philosophie … induktives Denken …

Die Ankündigung zur nächsten Sitzung am 9.Nov.2014 findet sich HIER.

Für einen Überblick über alle Blogeinträge zur Philosophiewerkstatt siehe HIER

Für einen Überblick über alle Blogeinträge nach Titeln siehe HIER

AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 15

Analytisch, Art (Spezies), Ausdruck - sprachlicher, Ausdruck - zusammengesetzter, Aussage, Aussagetypen, Außenraum zum Körper, Außenwelt, Avicenna, Bedeutung, Bedeutung - abstraktes Konstrukt, Bedeutung - akzidentell, Bedeutung - empirisch, Bedeutung - wesentliche, Bedeutung eines Wortes, Bedeutungsbeziehung, Bedeutungsraum, Definition, Definition - explitite, Definitorisch, Eigenschaft, Externe Welt, Falsch, Gattung (genus), Kategorien, Kognition, Logik, Logik - Alltag, Logik - Antike, Logik - formale, Logische Operatoren, Objekt, Objekt - als Eigenschaft, Objekt - echtes, Objekt - kontingent, Objekt - universell, Objekthierarchie, Objekttyp, Ontologie, ontologisch, Operator, Operator - aussagenlogischer, Prädikat, Proposition, Sein, Semantik, Subjekt, Subjekt - logisches, Wahr, Wahrheit, Wahrheit - definitorische (analytische), Wahrheit - ontologische, Wahrheit als Übereinstimmung, Wahrheitsbegriff, wahrheitsfähig, Wahrheitsgehalt, Wahrheitskriterium, Wahrheitswert

VORGESCHICHTE

Für einen Überblick zu allen vorausgehenden Beiträgen dieser rekonstruierenden Lektüre von Avicennas Beitrag zur Logik siehe AVICENNAS ABHANDLUNG ZUR LOGIK – BLITZÜBERSICHT.

Übersicht zum Wissen K bestehend aus Ausdrücken E, Objekten O sowie Bedeutungsbeziehungen M
Übersicht zum Wissen K bestehend aus Ausdrücken E, Objekten O sowie Bedeutungsbeziehungen M

WAHR UND FALSCHE AUSSAGEN

1. Nach dem Blogeintrag Avicenna 14b gibt es jetzt Ausdrücke A, B, …, die ‚wahr‘ oder ‚falsch‘ sein können und die wir deshalb ‚Aussagen‘ (auch ‚Propositionen‘) nennen. Aussagen können mittels aussagenlogischer Operatoren wie ‚NEGATION‘, ‚UND‘, ‚IMPLIKATION‘ usw. zu komplexeren Ausdrücken so verknüpft werden, dass jederzeit ermittelt werden kann, wie der Wahrheitswert des komplexen Ausdrucks lautet, wenn die Wahrheitswerte der Teilausdrücke bekannt sind. Ob im Einzelfall eine Aussage A ‚wahr‘ oder ‚falsch‘ ist, muss durch Rückgriff auf ihre Bedeutungsbeziehung M(A) geklärt werden. Bislang ist nur klar, dass die Bedeutungsbeziehung M nur allgemein eine Beziehung zu den (kognitiven) Objekten O herstellt (siehe Grafik oben).

2. Avicenna spricht aber nicht nur von Aussagen A allgemein, sondern unterscheidet die Teilausdrücke ‚Subjekt‘ S und ‚Prädikat‘ P, zusätzlich oft noch ‚Quantoren‘ Q.

FEINSTRUKTUR DER BEDEUTUNG VON AUSDRÜCKEN

3. Man kann und muss dann die Frage stellen, ob und wie sich auf der Bedeutungsseite die Unterscheidung in S und P auf der Ausdrucksseite widerspiegelt?

ECHTE UND UNECHTE OBJEKTE

4. In vorausgehenden Blogeinträgen zu Avicenna (Avicenna 4, 5, 7 und 11) wurde schon unterschieden zwischen ‚echten‘ und ‚unechten‘ Objekten. ‚Unechte Objekte‘ sind solche Wissenstatbestände, die man zwar identifizieren und unterscheiden kann, die aber immer nur im Kontext von ‚echten Objekten‘ auftreten. ‚Unechte‘ Objekte werden meistens als ‚Eigenschaften‘ bezeichnet. Beispiel: die Farbe ‚Rot‘ können wir wahrnehmen und z.B. von der Farbe ‚Blau‘ unterscheiden, die Farbe ‚Rot‘ tritt aber nie alleine auf so wie z.B. Gegenstände (Tassen, Stühle, Früchte, Blumen, …) alleine auftreten.

5. Hier wird davon ausgegangen, dass die Objekthierarchie O primär von echten Objekten gebildet wird; unechte Objekte als Eigenschaften treten nur im Kontext eines echten Objekts auf.

GATTUNG UND ART; KATEGORIEN

6. Ein Objekt kann viele Eigenschaften umfassen. Wenn es mehr als ein Objekt gibt – also O1, O2, … — die sowohl Eigenschaften Ex gemeinsam haben wie auch Eigenschaften Ey, die unterschiedlich sind, dann kann man sagen, dass alle Objekte, die die Eigenschaften Ex gemeinsam haben, eine ‚Gattung‘ (‚genus‘) bilden, und dass man anhand der ‚unterscheidenden Eigenschaften Ey‘ unterschiedliche ‚Arten‘ (’species‘) innerhalb der Gattung unterscheiden kann.

7. Gattungen, die keine Gattungen mehr ‚über sich‘ haben können, sollen hier ‚Kategorien‘ genannt werden.

ONTOLOGISCHE UND DEFINITORISCHE (ANALYTISCHE) WAHRHEIT

8. Bislang ist der Wahrheitsbegriff $latex \top, \bot$ in dieser Diskussion an der hinreichenden Ähnlichkeit eines vorgestellten/ gedachten kognitiven) Objekts $latex a \in Oa$ mit sinnlichen wahrnehmbaren Eigenschaften $latex s \subseteq Os$ festgemacht worden. Ein ‚rein gedachtes Objekt $latex a \in Oa$ ist in diesem Sinne weder ‚wahr‘ $latex \top$ noch ‚falsch‘ $latex \bot$.

9. Setzt man allerdings eine Objekthierarchie O voraus, in der man von einem beliebigen individuellem Objekt a immer sagen kann, zu welchem Objekt Y es als seiner Gattung gehört, dann kann man eine Aussagen der Art bilden ‚a ist eine Tasse‘.

10. Wenn man zuvor in einer Definition vereinbart haben sollte, dass zum Begriff der ‚Tasse‘ wesentlich die Eigenschaften Ex gehören, und das Objekt a hätte die Eigenschaften $latex Ex \cup Ey$, dann würde man sagen, dass die Aussage ‚a ist eine Tasse‘ ‚wahr‘ ist, unabhängig davon, ob es zum kognitiven Objekt a ein ’sinnliches‘ ‚Pendant‘ geben würde oder nicht. Die Aussage ‚a ist eine Tasse‘ wäre dann ‚rein definitorisch‘ (bzw. ‚rein analytisch‘) ‚wahr.

11. Im Gegensatz zu solch einer rein definitorischen (analytischen) Wahrheit eines Objekts a, die als solche nichts darüber sagt, ob es das Objekt a ‚tatsächlich‘ gibt, soll hier die ursprünglich vereinbarte ‚Wahrheit‘ durch Bezug auf eine ’sinnliche Gegebenheit‘ $latex s \subseteq Os$ ‚ontologische‘ Wahrheit genannt werden, also einer Wahrheit, die sich auf das ‚real Seiende‘ in der umgebenden Welt W bezieht.

12. [Anmerkung: Dieses – auch im Alltagsdenken – unterstellte ‚Sein‘, die unterstellte übergreifende ‚Realität‘ ist nicht nur eine ‚Extrapolation‘ aufgrund sinnlicher Gegebenheiten ‚im‘ wissenden System, sondern ist in seiner unterstellten ‚Realität‘ auch nur eine sehr spezifische Form von Realität. Wie wir heute aufgrund immer komplexerer Messprozeduren wissen, gibt es ‚Realitäten‘, die weit jenseits aller sinnlichen Qualitäten liegen. Es fällt uns nur nicht so auf, weil diese gemessenen Eigenschaften X durch allerlei Prozeduren für unsere Sinnesorgane ‚umgerechnet‘, ‚transformiert‘ werden, so dass wir etwas ‚Sehen‘ oder ‚Hören‘, obgleich das gemessene X nicht zu sehen oder zu hören ist.]

13. Solange wir uns in unseren Aussagen auf das Enthaltensein eines Objektes a in einem Gattungsobjekts X beschränken ‚a ist ein X‘ oder das Feststellen von Eigenschaften der Art ‚a hat b‘ kann man sagen, dass eine Aussagestruktur wie (S P) wie folgt interpretiert werden kann: Es gibt einen Ausdruck A=(AsAp), bei dem ein Ausdrucksteil As sich auf ein echtes Objekt M(As) = $latex a \in Oa$ bezieht und der andere Ausdrucksteil Ap bezieht sich auf die Beziehung zwischen dem Objekt a und entweder einem Gattungsobjekt X (Ap = ‚ist ein X‘) oder auf eine Eigenschaft Y (Ap = ‚hat Y‘).

14. Derjenige Ausdrucksteil As, der sich auf das echte Objekt a bezieht, ‚von dem‘ etwas ausgesagt werden soll (‚ist ein…‘, ‚hat …‘), dieser Ausdrucksteil wird als ‚Subjekt‘ S bezeichnet, und der Ausdrucksteil Ap, mittels dem etwas über das Subjekt ausgesagt wird, wird ‚Prädikat‘ P genannt.

15. Hierbei ist eine gewisse ‚Asymmetrie‘ zu beachten. Die Bedeutung vom Ausdrucksteil As – M(As) – bezieht sich auf eine ‚konkrete‘ Eigenschaftsstruktur innerhalb der Objekthierarchie. Die Bedeutung vom Ausdrucksteil Ap – M(Ap) – bezieht sich auf eine ‚Beziehung‘ / ‚Relation’/ ein ‚Verhältnis‘ [R] zwischen dem bezeichneten Bedeutungsobjekt M(As) = a und einem anderen bezeichneten Bedeutungsobjekt M(Ap), also R(M(As), M(Ap)). Die Beziehung R ist selbst kein ‚Objekt‘ so wie das Objekt a oder das implizit angenommene ‚Bezugsobjekt‘ X bzw. Y von a. Eine solche Beziehung R setzt – um prozessural ‚hantierbar‘ zu sein – eine zusätzliche ‚Objektebene‘ voraus, auf der es ein R-Objekt gibt, das die Beziehung zwischen dem a-Objekt und dem X-Y-Objekt ‚repräsentiert.

16. [Anmerkung: Bei ’neuronalen Netzen‘ wäre das R-Objekt jenes Neuron, das die Verbindung zwischen zwei anderen Neuronen ‚realisiert‘.]

17. Fassen wir zusammen: Bei einem Ausdruck A der Art A=’Hans ist ein Mensch‘ gibt es den Ausdrucksteil As=’Hans‘ und den Ausdrucksteil Ap=’ist ein Mensch‘. Die Bedeutung des Ausdrucksteils As M(As) als M(‚Hans‘) ist ein Objekt h in der unterstellten Bedeutungshierarchie O des Sprechers, das gewisse Eigenschaften E(h) besitzt. Die Bedeutung des Ausdrucksteils Ap als M(Ap) bzw. M(‚ist ein Mensch‘) ist sowohl ein Objekt M mit Eigenschaften E(M) als auch eine Beziehung R_ist zwischen dem Objekt h und dem Objekt M, also R_ist(h,M). Die Beziehung ist definitorisch/ analytisch ‚wahr‘ wenn es gilt, dass die definierenden Eigenschaften E(M) des Objekts Mensch M auch bei den Eigenschaften E(h) von Hans zu finden sind, also $latex E(M) \subset E(h)$ .

BEZIEHUNGSRAUM – TRANSZENDENTALE BEDINGUNGEN

18.

Fortsetzung folgt

QUELLEN

  • Avicenna, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
  • Digital Averroes Research Environment
  • Nicholas Rescher (1928 – ),The Development of Arabic Logic. University of Pittsburgh Press, 1964
  • Hans-Jörg Sandkühler (Hg.) unter Mitwirkung von Dagmar Borchers, Arnim Regenbogen, Volker Schürmann und Pirmin Stekeler-Weithofer, ‚Enzyklopädie Philosophie‘, 3 Bd., Hamburg: FELIX MEINER VERLAG, 2010 (mit CD-ROM)
  • Stanford Encyclopedia of Philosophy, Aristotle’s Logic
  • Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7

Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER

AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 14

Aussage, Aussagetypen, Außenraum zum Körper, Außenwelt, Avicenna, Bedeutung, Bedeutung - abstraktes Konstrukt, Bedeutung - empirisch, Bedeutung eines Wortes, Bedeutungsbeziehung, Bedeutungskorrelat, Bedeutungsmaterial, Bedeutungsraum, Erfüllung, Falsch, Logik, Logik - Alltag, Logik - Antike, Logische Operatoren, Möglichkeit, Notwendig, Operator, Operator - aussagenlogischer, Semantik, Wahr, Wahrheit, Wissen, Wissen - gefolgertes, Wissen - sensorisches, Wissen - sprachlich vermitteltes, Zutreffen

VORGESCHICHTE

Für einen Überblick zu allen vorausgehenden Beiträgen dieser rekonstruierenden Lektüre von Avicennas Beitrag zur Logik siehe AVICENNAS ABHANDLUNG ZUR LOGIK – BLITZÜBERSICHT.

1. Wenn also eine Formulierung von Konvertierungsregeln nicht ohne Bezug auf irgend eine Bedeutung M hinter den Ausdrücken möglich ist, stellt sich zum wiederholten Male die Frage, über welche mögliche Bedeutung M ‚hinter‘ den Ausdrücken gesprochen werden muss.

KONVERTIERUNG MIT BEDEUTUNG – MIT WELCHER?

2. Beginnen wir mit dem Ausgangspunkt, dass Aussagen PROP solche Ausdrücke von der Menge aller Ausdrücke E sind, die ‚wahr‘ oder ‚falsch‘ sein können. ‚Treffen sie zu‘ gelten sie als ‚wahr‘; ‚treffen sie nicht zu‘ gelten sie als ‚falsch‘.
3. Bislang hatten wir schon die generelle Annahme geäußert, dass das Denken und Wissen eines Menschen im ‚Innern‘ dieses Menschen zu verorten sei und der Mensch ‚in‘ einer umgebenden Welt W mit realen Ereignissen X vorkommt.
4. Um die Begriffe ‚wahr/ falsch‘ bzw. ‚zutreffen/ nicht zutreffen‘ zu ‚erklären‘, nehmen wir an, dass die Menge des möglichen Wissens K eines einzelnen Menschen sich zerlegen lässt in die Teilmengen ‚Vorgestellt‘ K_v, ‚Erinnert‘ K_m sowie ’sinnlich präsent‘ K_s. Es gilt also $latex K = K_{s} \cup M_{v} \cup M_{m}$.
5. Eine Bedeutung wird dann durch eine Beziehung zwischen dem Wissen K und möglichen Ausdrücken $latex PROP \subseteq E$ gebildet: $latex M \subseteq PROP \times K$.
6. Speziell gilt aber, dass man zwischen einer ’neutralen‘ Bedeutung $latex M_n \subseteq E \times (K_{v} \cup K_{m})$ unterscheiden muss, die weder ‚wahr‘ noch ‚falsch‘ ist, und der ’sinnlich fundierten‘ Bedeutung $latex M_s \subseteq E \times K_{s}$. Gibt es zwischen einer neutralen Bedeutung $latex M_{n}$ und einer sinnlich fundierten Bedeutung $latex M_{s}$ eine Beziehung des ‚Zutreffens‘ $latex M_{s} \models M_{n}$, dann kann man sagen, dass das Wissen $latex K_{n}$ in dieser Beziehung ‚wahr‘ ist, andernfalls nicht, geschrieben $latex M_{s} \not\models K_{n}$.
7. Zusätzlich kann man im Bereich des erinnerten Wissens $latex K_{m}$ noch unterscheiden zwischen einem solchen, das Bezug zu ‚vormals sinnlich fundiertem Wissen‘ aufweist als $latex K_{ms}$ und solchem, das ‚keinen Bezug zu vormals fundiertem sinnlichen Wissen‘ aufweist als $latex K_{mns}$.
8. Erinnertes Wissen mit Bezug zu vormals fundiertem Wissen $latex K_{ms}$ hat die Eigenart, dass sich in Abhängigkeit von der ‚Häufigkeit‘ der erinnerbaren Wissenselementen in $latex K_{ms}$ eine Art ‚Erwartung‘ bzgl. des neuerlichen Eintretens dieses Wissens als sinnliches Wissen $latex K_{vs}$ ausbildet: $latex \mu: K_{ms} \longrightarrow K_{vs}$ mit $latex K_{vs} \subseteq K_{v}$, d.h. im Bereich des vorgestellten Wissens $latex K_{v}$ gibt es solches mit einem speziellen Erwartungsanteil $latex K_{vs}$ hervorgerufen durch besondere Erinnerungen.

EXKLUSIVE MODALOPERATOREN

9. An dieser Stelle könnte man dann noch die Begriffe ‚möglich‘ $latex \diamond$ und ’notwendig‘ $latex \boxempty$ wie folgt einführen: ein vorgestelltes Wissen gilt als ‚möglich‘, wenn der Erwartungswert nicht gleich 1 ist, also $latex \diamond K_{v} \leftrightarrow \mu(K_{v}) \not= 1$, andernfalls als notwendig, also $latex \boxempty K_{v} \leftrightarrow \mu(K_{v}) = 1$
10. Daraus kann man ableiten, dass gelten soll $latex \boxempty K_{v} \leftrightarrow \neg\diamond K_{v}$ oder $latex \neg\boxempty K_{v} \leftrightarrow \diamond K_{v}$.
11. Diese Definition von ‚möglich‘ und ’notwendig‘ entspricht nicht ganz der ‚Intuition‘, dass etwas, was ’notwendig‘ ist, auf jeden Fall auch möglich sein sollte; allerdings folgt – intuitiv — aus der Möglichkeit keine Notwendigkeit. Die vorausgehende Definition von möglich und notwendig erinnert ein wenig an das ‚exklusive Oder‘, das auch ’schärfer‘ ist als das normale Oder. Nennen wie die hier benutzte Definition von ‚möglich‘ $latex \diamond$ und ’notwendig‘ $latex \boxempty$ daher auch die ‚exklusiven Modaloperatoren‘: Wenn etwas notwendig ist, dann ist es nicht möglich, und wenn etwas möglich ist, dann ist es nicht notwendig.
12. Anmerkung: wenn etwas ‚gedanklich notwendig‘ ist, folgt daraus in diesem Rahmen allerdings nicht, dass es auch tatsächlich sinnlich eintritt. Aus der gedanklichen Notwendigkeit folgt nur, dass es in der erinnerbaren Vergangenheit bislang immer eingetreten ist und daher die Erwartung sehr hoch ist, dass es wieder eintreten wird.

WAHR und FALSCH ABKÜRZUNGEN

13. Wenn man von einer Aussage $latex e \in E$ sagen kann, dass das zugehörige vorstellbare Wissen $latex M(e)=K_{v}$ ‚wahr‘ ist, weil es auf ein sinnliches Wissen $latex K_{s}$ ‚zutrifft oder eben ‚falsch‘, weil es ’nicht zutrifft‘, dann soll dieser Sachverhalt hier wie folgt abgekürzt werden:
14. Eine Aussage A soll genau dann mit ‚wahr‘ $latex \top$ bezeichnet werden, wenn es ein sinnliches Wissen gibt, das das zugehörige vorgestellte Wissen ‚erfüllt‘, also $latex (A)\top \leftrightarrow M(A)=K_{v}$ und es gibt ein sinnlich fundiertes Wissen $latex K_{s}$, so dass gilt $latex K_{s} \models K_{v}$.
15. Eine Aussage A soll genau dann mit ‚falsch‘ $latex \bot$ bezeichnet werden, wenn es kein sinnliches Wissen gibt, das das zugehörige vorgestellte Wissen ‚erfüllt‘, also $latex (A)\bot \leftrightarrow M(A)=K_{v}$ und $latex K_{s} \not\models K_{v}$. [Anmerkung: Es gibt nur ein einziges sinnlich fundiertes Wissen, und zwar das jeweils aktuelle!]

AUSSAGEOPERATOREN

16. Jetzt kann man folgende Operatoren über Aussagen definieren:
17. NEGATION: die Verneinung einer Aussage A ist wahr, wenn die Aussage selbst falsch ist, also $latex (\neg A)\top \leftrightarrow (A)\bot$.
18. KONJUNKTION: die Konjunktion $latex \wedge$ von zwei Aussagen A und B ist wahr, wenn beide Aussagen zugleich wahr sind; ansonsten ist die Konjunktion falsch, also $latex (A \wedge B)\top \leftrightarrow (A)\top\ und\ zugleich\ (B)\top$; ansonsten falsch.
19. DISJUNKTION: die Disjunktion $latex \vee$ von zwei Aussagen A und B ist wahr, wenn eine von beiden Aussagen wahr ist; ansonsten ist die Disjunktion falsch, also $latex (A \vee B)\top \leftrightarrow (A)\top\ oder\ (B)\top$; ansonsten falsch.
20. EXKLUSIVE DISJUNKTION: die exklusive Disjunktion $latex \sqcup$ von zwei Aussagen A und B ist wahr, wenn genau eine von beiden Aussagen wahr ist; ansonsten ist die exklusive Disjunktion falsch, also $latex (A \sqcup B)\top \leftrightarrow\ Entweder\ (A)\top\ oder\ (B)\top$; ansonsten falsch.
21. IMPLIKATION: die Implikation $latex \rightarrow$ von zwei Aussagen A und B ist wahr, wenn nicht A wahr ist und zugleich B falsch, also $latex (A \rightarrow B)\top \leftrightarrow\ nicht (A)\top\ und\ zugleich\ (B)\bot$; ansonsten falsch.

Fortsetzung folgt

QUELLEN

  • Avicenna, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
  • Digital Averroes Research Environment
  • Nicholas Rescher (1928 – ),The Development of Arabic Logic. University of Pittsburgh Press, 1964
  • Stanford Encyclopedia of Philosophy, Aristotle’s Logic
  • Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7

Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER.

AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 13

Allquantor, Avicenna, Bedeutung, Bedeutung eines Wortes, Bedeutungsbeziehung, Bedeutungskorrelat, Bedeutungsmaterial, Beweis - logischer, Falsch, Folgern - logisches, Konvertierung von Ausdrucksformen, Logik, Logik - Alltag, Logik - Antike, Logik - formale, Partikularquantor, Prädikat, Quantor, Quantor - partikulär, Quantor - universell, Semantik, Subjekt, Wahr, Wahrheit

(Letzte Änderung 8.Sept.2014, 02:59h)

VORGESCHICHTE

Für einen Überblick zu allen vorausgehenden Beiträgen dieser rekonstruierenden Lektüre von Avicennas Beitrag zur Logik siehe AVICENNAS ABHANDLUNG ZUR LOGIK – BLITZÜBERSICHT.

AVICENNAS DISKUSSION VON UMWANDLUNG (‚Conversion‘)

1. Aus der englischen Übersetzung ist nicht klar zu entnehmen, ob der Begriff ‚Umwandlung‘ (engl.: ‚conversion‘) tatsächlich eine Form von ‚Umwandlung’/ ‚Umformung’/ ‚Konvertierung‘ meint oder spezieller eine Umformung von Aussagen, die letztlich eine ‚logische Folgerung‘ darstellen. Letztere Interpretation wird angeregt, da er dann tatsächlich an entscheidender Stelle zum ersten Mal in der ganzen Abhandlung eine Folge von Aussagen präsentiert, die man als ‚Folgerungstext‘ interpretieren kann.

2. In seiner Kerndefinition gleich zu Beginn charakterisiert er den Ausdruck ‚Umformung‘ mit Bezug auf zwei Ausdrücke A und B, die Subjekte, Prädikate, Antezedenz und Konsequenz enthalten können (implizit auch Quantoren, da er diese im folgenden Text beständig benutzt). Jede der beiden Aussagen hat eine Bedeutung M(A) bzw. M(B). Umformung hat jetzt damit zu tun, dass einzelne dieser logischen Rollen (Q, S, P, …) ‚ausgetauscht‘ werden, ohne dass dadurch die ‚Bedeutung‘ verändert wird.

3. [Anmerkung: Hier gibt es folgende Unklarheiten: (i) Sollen die Bedeutungen M(A) und M(B) von vornherein ‚gleich‘ sein, und zwar so, dass sie nach dem Austausch unverändert sind? oder (ii) sind die Bedeutungen M(A) und M(B) von vornherein ungleich, sollen aber, jede für sich, auch nach der Umformung gleich sein? In beiden Fällen – so interpretiere ich seine Aussage von Avicenna, gibt es eine Bedeutung vor der Umformung – eine gemeinsame oder eine individuelle –, die nach der Umformung ‚gleich‘ geblieben ist. Schreiben wir für die Umformung als $latex \vdash$, dann würde bedeuten ‚$latex A \vdash B$‘ A wird nach B umgeformt, so dass die Bedeutung von A und B – gemeinsam oder individuell – erhalten bleibt. Es stellt sich hier wieder das Problem – wie im gesamten vorausgehenden Text –, dass der Begriff ‚Bedeutung‘ bei Avicenna nicht scharf definiert ist. Er kann alles und nichts bedeuten. Die ‚Gleichheit‘ von zwei Bedeutungen M_vorher und M_nachher ist also ein ‚offener Begriff‘.]

4. In dem folgenden Text präsentiert Avicenna einerseits einige Beispiele von Umformungen ohne genauere Begründungen, in einem Fall präsentiert er aber das Beispiel einer ausführlicheren Begründung, die wie eine Folgerungstext (wie ein logischer Beweis) aussieht. Beginnen wir mit den Beispielen ohne Begründung.

5. Mögliche Konversion: Von ‚Kein Mensch ist unsterblich‘ ($latex \neg\exists (Mensch)(ist)(unsterblich)$) kann man bedeutungserhaltend umformen in ‚Kein Unsterblicher ist ein Mensch‘ ($latex (\neg\exists (Unsterblicher)(ist)(Mensch)$).

6. Avicenna stellt die Regel auf: Von einer affirmativen All-Aussage kann ich nicht zu einer anderen affirmativen All-Aussage konvertieren.

7. Beispiel: Von ‚Jeder Mensch ist ein Lebewesen‘ kann ich nicht umformen zu ‚Jedes Lebewesen ist ein Mensch‘ (mehr formalisiert: ($latex \forall (Mensch)(ist)(Lebwesen)$) kann nicht umgeformt werden zu ($latex \forall (Lebewesen)(ist)(Mensch)$).

8. Avicenna stellt die Regel auf: Die Umformung einer affirmativen All-Aussage ist eine affirmative Partikular-Aussage.

9. Beispiel: Die Aussage ‚Alle F sind B‘ kann umgeformt werden zu ‚Einige B sind F‘ (Formalisierter: Den Ausdruck $latex \forall (F)(sind)(B)$) kann man umformen zu ($latex \exists(B)(ist)(F)$))

10. Avicenna stellt die Regel auf: Eine affirmative Partikular-Aussage kann umgeformt werden in eine affirmative Partikular-Aussage.

11. Beispiel: Der Ausdruck ‚Einige F sind B‘ kann umgeformt werden zu ‚Einige B sind F‘ (Formalisierter: ($latex \exists (F)(sind)(B)$) $latex \vdash$ ($latex \exists (B)(sind)(F)$)).

12. Avicenna stellt die Regel auf: Eine negative Partikular-Aussage kann nicht konvertiert werden.

13. Beispiel: Die Aussage ‚Kein Lebewesen ist ein Mensch‘ kann nicht konvertiert werden zu ‚Kein Mensch ist ein Lebewesen‘. (mehr formalisiert: ($latex \neg\exists (Lebewesen)(ist)(Mensch)$) $latex \not\vdash$ ($latex \neg\exists (Mensch)(ist)(Lebewesen)$))

14. [Anmerkung: Hier gibt es einigen Diskussionsbedarf. Bevor die Diskussion eröffnet wird, hier aber noch das Konvertierungsbeispiel, das wie ein Folgerungstext aussieht.]

15. Ausgangspunkt ist die Regel: Eine negative All-Aussage kann in eine negative All-Aussage konvertiert werden mit dem Beispiel: Von ($latex \neg\exists (Mensch)(ist)(Unsterblicher)$) $latex \vdash$ ($latex \neg\exists (Unsterblicher)(ist)(Mensch)$).

16. Avicenna nennt die nun folgende ‚Folge von Aussagen‘ explizit einen ‚Beweis‘ (engl.: ‚proof‘).

17. Wenn es ‚wahr‘ ist, dass gilt (Kein F ist B), dann ist es auch wahr, dass (Kein B ist F). Andernfalls [wäre der Wenn-Dann-Zusammenhang nicht wahr] würde der Widerspruch (engl.: ‚contradictory‘) folgen (Einige B sind F).

18. [Anmerkung: Zur Erinnerung, die Negation einer Implikation (Wenn A dann B) ist nur wahr, wenn A wahr wäre und zugleich B falsch, also ’nicht B‘, d.h. ’nicht(Kein B ist F)‘ d.h. (einige B sind F). Insofern bildet die Aussage (Einige B sind F) einen logischen Widerspruch zu (Kein B ist F). ]

19. Der Beweis beginnt damit, dass Avicenna eine Abkürzung einführt: Er definiert ‚H := ‚Einige B‘. [ein sehr gefährliches Unterfangen…]

20. Dann folgert er ‚H ist gleichbedeutend mit F‘

21. Er folgert weiter: ‚H ist sowohl F als auch B [Damit unterschlägt er, dass H eigentlich nur ‚einige‘ B meinen sollte]

22. Er folgert weiter: Dann gibt es ein F, das auch B ist ($latex \exists (F)(ist)(B)$

23. Er folgert weiter: Nehme ich die Aussage (Einige B sind F) als wahr an, dann komme ich zu der Aussage (Einige F sind B); dies steht aber im Widerspruch zu der Ausgangsbehauptung, das ‚Kein F ist B‘.

24. Er folgert weiter: Deshalb ist es nicht möglich, von der Ausgangsbehauptung ‚Wenn es ‚wahr‘ ist, dass gilt (Kein F ist B), dann ist es auch wahr, dass (Kein B ist F)‘ auf den Widerspruch ‚Einige F sind B‘ zu schließen.

25. Avicenna folgert weiter: Von daher, wenn es gilt, dass ‚Kein F ist B‘, dann gilt auch die Konvertierung ‚Kein B ist F‘.

DISKUSSION

KONVERTIERBARKEIT DER FORMEN (Q (A B)) zu (Q (B A)) – BEDEUTUNGSABHÄNGIG

26. In den Beispielen, die Avicenna präsentiert, gibt es zwei Beispiele, die verwirrend sind. Im einen Fall will er über ’negative All-Aussagen‘ ($latex \neg\forall$) sprechen und im anderen Fall über ’negative Partikular-Aussagen‘ ($latex \neg\exists$). Das Beispiel für negative All-Aussagen lautet ‚Kein Mensch ist unsterblich‘. Der Quantor ‚kein‘ ist aber definiert als ’nicht einige‘ bzw. ‚$latex \neg\exists$‘. Dies aber ist gleichbedeutend mit einer negativen Partikular-Aussage. Später präsentiert er als Beispiel für negative Partikular-Aussagen den Ausdruck ‚Kein Lebewesen ist ein Mensch‘ ($latex \neg\exists (Lebewesen)(ist)(Mensch)$).

27. Damit haben wir es mit folgenden Widersprüchlichkeiten zu tun: (i) Avicenna interpretiert seinen Begriff der negativen Allaussagen mit einem Beispiel, das eine negative Partikular-Aussage repräsentiert; (ii) Mit einem Beispiel, das eine negative Partikular-Aussage repräsentiert, argumentiert er, dass man bedeutungserhaltend negative All-Aussagen konvertieren kann; (iii) Mit einem anderen Beispiel einer negativen Partikularaussage argumentiert er, man könne dieses nicht konvertieren.

28. Da das Beispiel zu (ii) zeigt, dass man sehr wohl eine negative Partikular-Aussage konvertieren kann, fragt man sich, warum es in einem anderen Fall nicht gehen soll. Dazu kommt, dass das konkrete Beispiel, das Avicenna präsentiert, aus sich heraus fragwürdig erscheint: ‚Kein Lebewesen ist ein Mensch‘ soll nicht konvertierbar sein zu ‚Kein Mensch ist ein Lebewesen‘. (mehr formalisiert: ($latex \neg\exists (Lebewesen)(ist)(Mensch)$) $latex \not\vdash$ ($latex \neg\exists (Mensch)(ist)(Lebewesen)$))

29. Bekannt ist – zumindest bezogen auf diese Begriffe –, dass sehr wohl einige Lebewesen Menschen sind, also eher gilt $latex \neg\neg\exists (Lebewesen)(ist)(Mensch)$, d.h. $latex \exists (Lebewesen)(ist)(Mensch)$. Von einer Aussage wie $latex \neg\exists (Mensch)(ist)\neg(Lebewesen)$) könnte man allerdings nicht konvertieren zu $latex \neg\exists (Lebewesen)(ist)\neg(Mensch)$).

30. Trotzdem gibt es eine mögliche Konvertierung von ($latex \neg\exists (Mensch)(ist)(Unsterblich)$)) zu ($latex \neg\exists (Unsterblich)(ist)(Mensch)$)).

31. Diese Beispiele legen die Vermutung nahe, dass die bisherigen ‚Konvertierungsregeln‘ von Avicenna nicht unabhängig sind von der jeweils unterstellten Bedeutung der beteiligten Subjekte und Prädikate.

32. Bezogen auf die Struktur (Q (A B)) $latex \vdash (Q (B A))$ hängt die Möglichkeit oder Unmöglichkeit einer Konvertierung in den Beispielen davon ab, wie sich die Bedeutungen von A und B, also M(A) und M(B), zueinander verhalten.

33. Zwei Hauptfälle kann man unterscheiden: (i) die Bedeutung von beiden Ausdrücken ist ‚gleich‘, d.h. M(A) = M(B), oder (ii) die Bedeutungen sind ungleich in dem Sinne, dass zwar alle Elemente, die zu M(B) gehören auch in M(A) sind, aber nicht umgekehrt, also $latex M(B) \subseteq M(A)$.

34. Wenn wir Fall (i) M(A) = M(B) unterstellen können, dann kann man von $latex \forall A sind B$ auf $latex \forall B sind A$ schließen, oder $latex \exists A sind B$ und umgekehrt. Die Aussage $latex \neg\forall A sind B$ wäre formal zwar möglich, wäre aber ’semantisch‘ (aufgrund der angenommenen Bedeutung) aber nicht möglich. Genau sowenig wie $latex \neg\exists A sind B$ semantisch möglich wäre, wohl aber syntaktisch.

35. Unterstellen wir hingegen den Fall (ii) $latex M(B) \subseteq M(A)$, dann würde die Konvertierung von $latex \forall A sind B$ auf $latex \forall B sind A$ nicht gelten. Entsprechend kann man die wahre Aussage $latex \forall B sind A$ nicht konvertieren zu $latex \forall A sind B$. Die Konvertierung $latex \exists A sind B$ würde gehen wie auch umgekehrt. Die Aussage $latex \neg\forall A sind B$ ist wahr, die Konvertierung zu $latex \neg\forall B sind A$ wäre falsch. Usw.

36. Diese Beispiele verdeutlichen, dass die Konvertierbarkeit von Ausdrücken der Form (Q (A B)) zu (Q (B A)) eindeutig von der angenommenen Bedeutungsstruktur abhängig ist (zumindest in dem Kontext, den Avicenna diskutiert). Betrachten wir seine anderen Konvertierungsregeln.

37. (i) Von einer affirmativen All-Aussage kann ich nicht zu einer anderen affirmativen All-Aussage konvertieren.

38. (ii) Die Umformung einer affirmativen All-Aussage ist eine affirmative Partikular-Aussage.

39. (iii) Eine affirmative Partikular-Aussage kann umgeformt werden in eine affirmative Partikular-Aussage.

40. (iv) Eine negative Partikular-Aussage kann nicht konvertiert werden.

41. Zu (i): Nehmen wir an, dass gilt ($latex M(A) = M(B)$), dann trifft diese Regel zu. Nehmen wir aber an, dass gilt ($latex M(B) \subseteq M(A)$), dann gilt diese Regel nicht.

42. Zu (ii) und (iii): Nehmen wir an, dass gilt ($latex M(A) = M(B)$), dann trifft diese Regel zu. Nehmen wir aber an, dass gilt ($latex M(B) \subseteq M(A)$), dann gilt diese Regel auch.

43. Zu (iv): Dieser Fall ist von der Form her (rein syntaktisch) möglich, von der Bedeutung her (rein semantisch) aber ausgeschlossen.

44. Bei allen bisherigen Konvertierungsbeispiele von Avicenna ist zu beachten, dass sich die Bedeutung des Subjekts S und des Prädikats P in einer Aussage (S P) in der Art $latex M(A) = M(B)$ oder $latex M(B) \subseteq M(A)$ beschreiben lässt. Dies setzt voraus, dass sich ein Prädikat P auch als eine Menge von Objekten auffassen lässt, denen eine bestimmte Eigenschaft E zukommt, also etwa P := ‚eine Menge von Elementen, die die Eigenschaft P haben‘. Zu sagen ‚S ist P‘ würde dann sagen, dass die Elemente die S sind auch die Elemente sind, die P sind.

45. Man muss hier die Frage stellen, ob Prädikate immer diese Form haben.

KONVERTIERUNG OHNE BEDEUTUNG?

46. Macht man die Konvertierbarkeit von Ausdrücken der Form (Q (A B)) und (Q (B A)) von der Bedeutung M der Ausdrücke A und B abhängig, dann hängt die Formulierung der Konvertierungsregeln ab von einer brauchbaren Definition des zugrundeliegenden Bedeutungsraumes samt seiner Interaktion mit den Ausdrucksformen. Im weiteren Verlauf soll dies explizit untersucht werden. Es stellt sich aber auch die Frage, ob man Konvertierungsregeln nicht auch ohne Rückgriff auf die Bedeutung der Teilausdrücke formulieren kann.

47. Hat man nur die Ausdrücke (Q (S P)) mit der Verallgemeinerung, dass S und P ‚gleichwertig‘ sein können im Sinne von (Q (A B)) $latex \vdash$ (Q (B A)), dann stellt sich die Frage welche Kriterien man hätte, gäbe es keinen Bedeutungsbezug?

48. Man muss feststellen, dass ohne irgendeinen Bedeutungsbezug die Ausdrücke als solche keinerlei Ansatzpunkt bieten, eine Konvertierung zuzulassen oder sie zu verbieten.

49. Wenn aber Konvertierungsregeln ohne Bedeutung keinen Sinn machen, dann muss man sich fragen, welche Bedeutungsstrukturen man benötigt, dass man solche Konvertierungsregeln sinnvoll einführen kann.

KONVERTIERUNG MIT BEDEUTUNG – MIT WELCHER?

50. Wenn es also ohne Bezug auf eine Bedeutung nicht geht, stellt sich die Frage, wie eine solche Bedeutungsstruktur aussehen muss, damit solche – oder auch andere – Konvertierungsregeln formuliert werden können.

51. Die weitere Diskussion wird in einem neuen Blogeintrag fortgeführt werden.

Fortsetzung folgt

QUELLEN

  • Avicenna, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
  • Digital Averroes Research Environment
  • Nicholas Rescher (1928 – ),The Development of Arabic Logic. University of Pittsburgh Press, 1964
  • Stanford Encyclopedia of Philosophy, Aristotle’s Logic
  • Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7

Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER.

AVICENNAS ABHANDLUNG ZUR LOGIK – BLITZÜBERSICHT

Allgemein, Allquantor, Alltagssprache, Analytisch, Annahme, Art (Spezies), Ausdruck, Ausdruck - einfacher, Ausdruck - sprachlicher, Ausdruck - zusammengesetzter, Aussage, Aussagetypen, Außenraum zum Körper, Außenwelt, Avicenna, Bedeutung, Bedeutung - akzidentell, Bedeutung - empirisch, Bedeutung - kontingent, Bedeutung - wesentliche, Bedeutung eines Wortes, Bedeutungsbeziehung, Bedeutungskorrelat, Bedeutungsraum, Begriffe, Definiendum, Definiens, Definition, Definition - explitite, Definition - rekursive, Definition - simultane, Denken, Eigenschaft, Erinnerung, Evolution - biologische, Evolution - kognitive, Externe Welt, Folgern - logisches, Folgerung, Logik, Logik - Alltag, Logik - Antike, Logik - formale, Prädikat, Prämisse, Subjekt, Subjekt - logisches, Syllogismus, Syllogismus - Konjunktiver, Term

(Letzte Änderung 14.Okt.2014, 06:11h )

Da die rekonstruierende Lektüre zu Avicennas Abhandlung zur Logik ein immer größeres Ausmaß annimmt, erweist sich die Methode, jeden einzelnen Beitrag mit einem Überblick über die vorausgehenden Beiträge einzuleiten, als immer weniger praktikabel. Deswegen wird jetzt ein eigener Blogeintrag als Referenzpunkt für diesen Überblick gewählt. Dies bedeutet, dass künftig alle nachfolgenden Beiträge einleitend (für die ‚Vorgeschichte‘), auf diesen Blogeintrag verweisen werden. Es ist zu beachten, dass diese Übersicht nur eine Übersicht über die wichtigsten Begriffe und Themen ist ohne alle Details und normalerweise auch ohne die ausführliche Diskussion von Avicennas Gedanken. Diese finden sich nur in den Blogeinträgen selbst, auf die verwiesen wird.

1. In einem ersten Beitrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 1 hatte ich geschildert, wie ich zur Lektüre des Textes von Avicenna gekommen bin und wie der Text grob einzuordnen ist.

2. In einem zweiten Beitrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 2 ging es um die Frage, warum überhaupt Logik? Avicenna führt erste Unterscheidungen zu verschiedenen Wissensformen ein, lässt aber alle Detailfragen noch weitgehend im Dunkeln.

3. Im Teil AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 3 ging es um einfache und zusammengesetzte Begriffe, und bei den einfachen Begriffen um ‚individuelle‘ und ‚universelle‘. Schon hier zeigt sich der fundamentale Unterschied zwischen der antiken und der modernen-formalen Logik. In der antiken Logik wird die Ausdrucksebene E – und einer sich daran manifestierenden Folgerungslogik – immer in Verbindung mit einer zugehörigen Bedeutungsstruktur gesehen, die sich an einer Objektstruktur O festmacht. Die moderne formale Logik kennt zwar auch ‚Semantiken‘ und ‚Ontologien‘, diese sind aber ’sekundär‘, d.h. es werden nur solche ‚formalen Semantiken‘ betrachtet, die zum vorausgesetzten syntaktischen Folgerungsbegriff ‚passen‘. Dies sollte dann später an konkreten Beispielen diskutiert werden. Hier liegt der Fokus auf der antiken Logik im Sinne Avicennas.

4. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 4 knüpft Avicenna an den zuvor eingeführten Begriff des ‚universellen‘ Begriffs an und betrachtet jetzt solche als ‚universell‘ bezeichneten Ausdrücke in einem Ausdruckskontext von aufeinanderfolgenden Ausdrücken. Alle diese Ausdrücke könnte man im Sinne der antiken Logik auch als ‚Urteile‘ bezeichnen, durch die einem bestimmten Ausdruck durch andere Ausdrücke bestimmte Bedeutungen (Eigenschaften) zu- oder abgesprochen werden. Hier unterscheidet er die Fälle eines ‚wesentlichen‘ Zusammenhanges zwischen zwei Begriffen und eines ’nicht wesentlichen‘ – sprich ‚akzidentellen‘ – Zusammenhangs.

5. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 5 führt Avicenna eine Reihe von neuen technischen Begriffen ein, die sich nicht alle in ihrer Bedeutung widerspruchsfrei auflösen lassen. Es handelt sich um die Begriffe ‚Genus‘, ‚Spezies‘, Differenz, allgemeine und spezielle Akzidens, den Begriff ‚Kategorie(n)‘ mit den Kategorien ‚Substanz‘, ‚Qualität‘ und ‚Quantität‘. Die Rekonstruktion führt dennoch zu spannenden Themen, z.B. zu einem möglichen Einstieg in das weltverändernde Phänomen der kognitiven Evolution.

6. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 6 geht es um die Begriffe ‚Definition‘ und ‚Beschreibung‘. Im Verhältnis zwischen beiden Begriffen geht die Beschreibung der Definition voraus. In der ‚Definition‘, die Avicenna vorstellt, wird ein neuer Ausdruck e mittels anderer Ausdrücke <e1, …, ek>, die sich auf schon bekannte Sachverhalte beziehen, ‚erklärt‘. Die von Avicenna dann vorgenommene Erklärung, was eine ‚Definition‘ sei, hängt u.a. stark ab von dem Begriff der ‚Bekanntheit‘ und dem Begriff des ‚wahren Wesens‘. Für die Tatsache, dass ein Mensch A bestimmte Ausdrücke <e1, …, ek> einer Sprache L ‚kennt‘ oder ’nicht kennt‘, dafür gibt es keine allgemeinen Regeln oder Kriterien. Von daher macht die Verwendung der Ausdrücke ‚bekannt’/ ’nicht bekannt‘ eigentlich nur Sinn in solch einem lokalen Kontexten W* (z.B. einem Artikel, ein Buch, ein Vortrag, …), in dem entscheidbar ist, ob ein bestimmter Ausdruck e einer Sprache L schon mal vorkam oder nicht. Schwierig wird es mit dem Begriff des ‚wahren Wesens‘. In meiner Interpretation mit der dynamischen Objekthierarchie gibt es ‚das wahre Wesen‘ in Form von Objekten auf einer Stufe j, die Instanzen auf Stufen kleiner als j haben. Dazu gab es weitere Überlegungen.

7. Im folgenden Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 7 beschreibt Avicenna syntaktisch zusammengesetzte, aber semantisch einfache Ausdrücke. Innerhalb der Ausdrücke unterscheidet er die Teileausdrücke ‚Name‘, ‚Verb‘ und ‚Präposition‘. Die unterschiedliche Charakterisierung erfolgt nicht aufgrund der syntaktischen Form, sondern aufgrund der semantischen Eigenschaften, die mit diesen Ausdrücken verbunden werden. Neben dem Objektbezug, der die eigentliche Bedeutung fundiert, gibt es im Bedeutungsraum auch noch den zeitlichen und den räumlichen Aspekt. Das Zusammenspiel von Bedeutung und Ausdruck wird angerissen.

8. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 8 geht es um solche Ausdrücke E, die ‚Aussagen‘ P sind, von denen man sagt, dass sie ‚wahr‘ oder ‚falsch‘ seien. Aussagen sind eine echte Teilmenge aller Ausdrücke, $latex P \subset E$. Avicenna unterscheidet drei Arten von Aussagen: ‚kategorische‘ Aussagen, ‚Disjunktiv-konditionelle‘ und ‚Konjunktiv-konditionelle‘. Es wird ausführlich eine mögliche Wahrheitstheorie für die Zuschreibung ‚wahr’/ ‚falsch‘ diskutiert. Dann werden nochmals die Aussagetypen näher untersucht. Ein Zusammenhang mit der modernen Aussagenlogik wird hergestellt. Disjunktion, Konjunktion (und ergänzend) Implikation) sind Aussagetypen, die aus zwei Teilausdrücken A und B bestehen, die selbst wieder Aussagen sind, die wahr oder falsch sein können. Die beiden Teilausdrücke A und B werden dann durch die Teilausdrücke (oder), (und) sowie (wenn)-(dann)- verknüpft. Sie unterscheiden sich dadurch, wie der Wahrheitswert des Gesamtausdrucks von der Verteilung der Wahrheitswerte auf die Teilausdrücke festgelegt ist. Die Teilausdrücke (oder), (und) sowie (wenn)-(dann)- nennt man später dann auch ‚aussagenlogische Operatoren‘. Der Aussagetyp ‚kategorisierend‘ passt nicht in dieses Schema. Der Aussagetyp ‚kategorisierend‘ ist eine Aussage A, die wahr oder falsch sein kann unabhängig von irgendeinem aussagenlogischen Operator. Auch wird die Verneinung/ Negation diskutiert. Ausdrücke wie (Etwas)(ist nicht)(dies)(oder)(jenes) wurden rekonstruiert als $latex \neg(A)(oder)(B)$ mit dem Zeichen $latex \neg$ für ’nicht‘ oder ‚es ist nicht der Fall, dass‘.

9. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 9 kommt Avicenna auf mehrere Begriffspaare zu sprechen, die sich z.T. mit Themen berühren, die er schon vorher besprochen hat, z.T. neue Aspekte thematisieren, die nicht so ohne weiteres mit dem bisher Gesagten harmonieren. Es handelt sich z.B. um die Begriffe ‚Kategorisch‘, ‚Negation‘, ‚Universal‘, ‚Partikulär‘, die aber jetzt mit neuen Randbedingungen nochmals diskutiert werden. So stellt er die Frage, wann ‚kategorischen‘ (‚kategorisierenden‘) Aussagen ‚affirmativ‘ und wann sie ’negativ‘ sind. Ferner führt er neben den bisherigen die semantisch motivierten Begriffe ‚Name‘, ‚Verb‘ (auch ‚Term‘ genannt), sowie ‚Präposition‘ nun auch das Begriffspaar ‚Subjekt‘ und ‚Prädikat‘. Auch diese sind ’semantisch‘ motiviert, d.h. nur durch Rückgriff auf die Bedeutung kann man zur Klassifikation ‚Subjekt‘ bzw. ‚Prädikat‘ kommen. In den soeben erwähnten Kontexten wie auch in nachfolgenden Beispielen diskutiert Avicenna auch die Begriffe ‚affirmativ‘ und ’negativ‘. Zwischendrin bemerkt er auch mal, dass das Treffen einer Feststellung, eigentlich nur Sinne mache, wenn dasjenige, von dem etwas ausgesagt wird, auch existiere. Doch wird dieser Punkt nicht weiter diskutiert. Vom Subjekt einer Aussage sagt Avicenna, dass es partikulär‘ oder ‚universell‘ sein kann. Falls universell, dann kann man unterscheiden, ob sie ‚unbestimmt‘ (engl.: ‚indeterminate‘) ist – wie viele genau involviert sind — oder eben ‚bestimmt‘ (engl.: ‚determinate‘). Ferner illustriert er am Beispiel der kategorisierenden Aussagen auch die Begriffe ’notwendig‘ und ‚kontingent‘. Diese Verwendung der Begriffe stimmt überein mit den zuvor eingeführten Begriffe ‚wesentlich‘ und ‚akzidentell‘. Auch erwähnt Avicenna den Begriff ‚möglich‘. Er sieht mindestens zwei Verwendungsweisen von ‚möglich‘: In der Diskussion dieses Abschnitts werden einerseits einige Widersprüchlichkeiten in den Ausführungen Avicennas sichtbar gemacht, andererseits wird die Rekonstruktion einer möglichen systematischen Theorie zur Logik Avicennas fortgesetzt. Die wichtigsten Kritikpunkte kreisen um das Begriffspaar ‚affirmativ – negativ‘ mit der Kritik, dass beide Begriffe auf unterschiedlichen semantischen Ebenen liegen. Ferner widerspricht die Handhabung der Quantoren durch Avicenna der allgemeinen Verwendung.

10. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 10 diskutiert Avicenna seine Begriffe ‚Konjunktives‘ und ‚Disjunktives Konditional‘ unter verschiedensten Aspekten. Einige davon sind die Quantoren (wobei er auch Quantoren über die Zeit benutzt!), das Begriffspaar ‚Antezedenz – Konsequenz‘, der Begriff der ‚Harmonie‘, und wiederholt die Aspekte ‚Existenz‘, ‚Affirmation‘ sowie ‚Bestimmt/ Unbestimmt‘. Alle diese Aspekte werden in diesem Blogeintrag schon ein wenig ‚vorsortiert‘, um dann im nachfolgenden Blogeintrag weiter rekonstruierend diskutiert zu werden.

11. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 11 erfolgt eine ‚rekonstruierende Diskussion‘ von Avicennas Überlegungen aus Blogeintrag 10. Seine Überlegungen werden aufgegriffen und in einen theoretischen Rahmen eingeordnet, der es erlaubt, die Begriffe schärfer zu fassen und sie dadurch besser voneinander abzugrenzen. Nach einer Übersicht über die Struktur der Aussagen erfolgt dann eine Rekonstruktion von Bedeutungszuordnungen und eine Erklärung von Begriffen wie ‚wahr’/ ‚falsch‘, ‚Existenz‘, und ‚möglich‘.

12. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 12 diskutiert Avicenna den Fall widersprüchlicher Aussagen. Gemessen an dem bisher Gesagten bringt er in diesem Abschnitt keine neuen Aspekte ins Spiel. Wohl aber bietet dieser Abschnitt weitere Beispiele für sein Auffassung des Sachverhalts. Sie belegen, wie schwer er sich durchgängig damit tut, in dem unscharfen Wechselspiel von Ausdrucksseite und Bedeutungsseite eine konstante Verwendungsweise seiner Begriffe durchzuhalten. In diesem Blogeintrag erfolgt die Diskussion seines Textes immer unmittelbar hinter jedem Punkt in Form einer Anmerkung.

13. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 13 diskutiert Avicenna die Möglichkeit der Konvertierung von Aussagen mit Quantoren in solche, deren Bedeutung trotz Veränderung von Ausdruckselementen ‚erhalten‘ bleibt. In einigen Beispielen widerspricht er sich selbst; manche Stellen sind unklar. Es zeigt sich allgemein: (i) die Formulierung von Konvertierungsregeln greift beständig auf bestimmte unterstellte Bedeutungen zurück und (ii) genau diese unterstellten Bedeutungen werden nicht hinreichend klar definiert. Daraus entsteht die Forderung, diese unterstellte Bedeutung klar zu definieren und auf dieser Basis alle logischen Ausdruckselemente eindeutig zu definieren (was im nachfolgenden Abschnitt dann unternommen wird).

14/14b. In den Blogeinträgen AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 14 sowie AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 14b geht es darum, erstmalig einen theoretischen Rahmen für eine Semantik zu formulieren, mit der man die Logik Avicennas konsistent entwickeln kann. Abschnitt 14b stellt eine Überarbeitung des Eingangsteils von Abschnitt 14 dar. Es hat sich gezeigt, dass die in 14b gewählte Begrifflichkeit für das weitere Vorgehen ‚günstiger‘ wirkt. Aber wir befinden uns noch in der Phase der ‚Annäherung‘ an das ‚Neue‘.

15. In dem Blogeintrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 15 geht es um die Feinstruktur von Aussagen. Avicenna unterteilt ja Ausdrücke anhand inhaltlicher Kriterien nach Subjekt S, Prädikat P und ergänzend nach Quantoren Q. Es fragt sich, wie man diesen Ausdrucksteilen eine ‚Bedeutung‘ im Objektraum O zuordnen kann. Wichtig ist hier die schon früher getroffene Unterscheidung zwischen ‚echten‘ und ‚unechten‘ Objekten. ‚Unechte‘ Objekte wurden als ‚Eigenschaften‘ bezeichnet. Mit dieser Terminologie kann man sagen, dass die Objekthierarchie O primär von echten Objekten gebildet wird; unechte Objekte als Eigenschaften treten nur im Kontext eines echten Objekts auf. Damit kann man die begriffe ‚Gattung‘ und ‚Art‘ einführen. Gattungen, die keine Gattungen mehr ‚über sich‘ haben können, sollen hier ‚Kategorien‘ genannt werden. Setz man Definitionen von Worten voraus, dann kann man ach erklären, warum eine Aussage wie ‚a ist eine Tasse‘ ‚rein definitorisch‘ (bzw. ‚rein analytisch‘) ‚wahr ist, unabhängig davon, ob diesem gedanklichen Sachverhalt etwas Sinnliches entspricht. Im Gegensatz zu solch einer rein definitorischen (analytischen) Wahrheit eines Objekts a soll hier die ursprünglich vereinbarte ‚Wahrheit‘ durch Bezug auf eine ’sinnliche Gegebenheit‘ $latex s \subseteq Os$ ‚ontologische‘ Wahrheit genannt werden. Solange wir uns in unseren Aussagen auf das Enthaltensein eines Objektes a in einem Gattungsobjekts X beschränken ‚a ist ein X‘ oder das Feststellen von Eigenschaften der Art ‚a hat b‘ kann man sagen, dass eine Aussagestruktur wie (S P) wie folgt interpretiert werden kann: Es gibt einen Ausdruck A=(AsAp), bei dem ein Ausdrucksteil As sich auf ein echtes Objekt M(As) = $latex a \in Oa$ bezieht und der andere Ausdrucksteil Ap bezieht sich auf die Beziehung zwischen dem Objekt a und entweder einem Gattungsobjekt X (Ap = ‚ist ein X‘) oder auf eine Eigenschaft Y (Ap = ‚hat Y‘). Hierbei ist eine gewisse ‚Asymmetrie‘ zu beachten. Die Bedeutung vom Ausdrucksteil As – M(As) – bezieht sich auf eine ‚konkrete‘ Eigenschaftsstruktur innerhalb der Objekthierarchie. Die Bedeutung vom Ausdrucksteil Ap – M(Ap) – bezieht sich auf eine ‚Beziehung‘ / ‚Relation’/ ein ‚Verhältnis‘ [R] zwischen dem bezeichneten Bedeutungsobjekt M(As) = a und einem anderen bezeichneten Bedeutungsobjekt M(Ap), also R(M(As), M(Ap)). Die Beziehung R ist selbst kein ‚Objekt‘ so wie das Objekt a oder das implizit angenommene ‚Bezugsobjekt‘ X bzw. Y von a. Eine solche Beziehung R setzt – um prozessural ‚hantierbar‘ zu sein – eine zusätzliche ‚Objektebene‘ voraus, auf der es ein R-Objekt gibt, das die Beziehung zwischen dem a-Objekt und dem X-Y-Objekt ‚repräsentiert.

16. In dem Blogeintrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 16 wird die Analyse der vorausgesetzten Objekthierarchie O und der damit interagierenden Ausdrucksstruktur E weiter analysiert. Nach der Analyse der Feinstruktur von (S P) werden die Aspekte Anzahl, Raum und Zeit betrachtet. Es wird gezeigt, wie man für diese Aspekte sowohl ‚globale Quantoren‘ wie auch ‚lokale Relationen‘ einführen kann; zudem ist die Wechselwirkung zwischen diesen Aspekten konfliktfrei, da sie voneinander unabhängig sind.

17. In dem Blogeintrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 17 geht es um die Frage, wie man Aussagen über Veränderungen in der hypothetisch angenmmenen Bedeutungsstruktur nachzeichnen kann. Es lässt sich erkennen, dass die Kodierung von Veränderungen mittels Ausdruckselementen innerhalb eines Prädikates P mittels ‚Veränderungsausdrücken‘ V (‚Verben‘) oft nicht nur die beteiligten Objekte Y benennt, sondern zusätzlich zahlreiche weitere Ausdruckselemente aktiviert, die räumliche Gegebenheiten R_r bezeichnen, zeitliche Relationen R_t, zusätzliche Eigenschaften At an den Veränderungen; dazu ferner spezielle kulturelle Relationen R_x einbeziehen können sowie mit zusätzlichen Subjektrepräsentationen operieren. Auch kann man beobachten, wie die Aneinanderreihung von unterschiedlichen Sachverhalten (S P) mit logischen Operatoren (S P) UND (S2 P2) auch zu speziellen Verkürzungen führen kann wie (S P1 UND P2). Dies lässt erahnen, dass eine vollständige Analyse auch nur einer einzigen Alltagssprache von ihrer logisch relevanten Semantik her eine schier unendliche Aufgabe ist. Diese wird weder ein einzelner Mensch alleine noch viele Menschen über viele Genrationen hinweg jemals vollständig erfüllen können. Was aber möglich erscheint, das ist die Analyse des grundlegenden Mechanismus, der sich mit Hilfe von evolvierenden Computermodellen experimentell untersuchen und mit realen semiotischen Systemen überprüfen lässt.

18. In dem Blogeintrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 18 weitet sich nun der Blick Avicennas auf das Wissen allgemein, und konzentriert sich im Wissen auf das schlussfolgernde Denken in Form von ‚beweisenden Syllogismen‘. Nach einer Definition von ‚Syllogismus‘ unterscheidet er dann zwei Arten von Syllogismen ‚Konjunktiver‘ Syllogismen und ‚Disjunktiver‘ Syllogismus. Am Beispiel des ‚Konjunktiven Syllogismus‘ führt Avicenna dann eine Reihe von technischen Begriffen ein. Dann stellt Avicenna zusätzliche Beschränkungen vor, um die 256 möglichen Figuren/ Muster auf nur 27 mögliche Muster einzuschränken. Alle seine Festlegungen geschehen ohne eigentliche Begründung.

19. In dem Blogeintrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 19 beginnt die Diskussion um die Interpretation der syllogistischen Schlussfiguren am Beispiel der ersten Figur (A F B), (A B H) und (A F H) mit der Quantorenbelegung ‚AAA‘. In einzelnen Schritten wird dann eine erste Skizze zu einer Logik auf der Basis einer dynamischen Objektstruktur erarbeitet. Zentrale Begriffe sind hier OBJEKTIFIZIERUNG, ENTHALTENSEIN, ZUSCHREIBUNG und VERERBUNG. In dieser Skizze werden auch ‚Aktivitäten‘ berücksichtigt, die in dem Muster zur ersten Figur nicht vorkommen, zusätzlich werden neben den Anzahlquantoren auch Raum- und Zeitquantoren berücksichtigt.

20. In dem Blogeintrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 20 geht es um die Interpretation des zweiten Musters der ersten syllogistischen Schlussfigur ‚A F ist B‘, ‚A B ist nicht H‘ (als ‚Kein A ist B‘), ‚A F ist nicht H‘ (als ‚Kein F ist H‘), dazu die Beispiele ‚Jeder ausgedehnte Körper ist farbig‘, ‚Kein farbiger Körper ist unerschaffen‘, ‚Kein ausgedehnter Körper ist unerschaffen‘. Wir treffen in diesem Muster wieder auf den Prozess der Objektifizierung, tatsächlich sogar in impliziten Formen mit der expliziten Angabe von Eigenschaften und der stillschweigenden Annahme einer daraus sich ergebenden Mengenbildung. Zusätzlich finden sich wieder Enthaltensbeziehungen einerseits anhand von Eigenschaftszuschreibungen, andererseits durch Benutzung von Anzahlquantoren. Die Zuschreibung von Eigenschaften wird explizit vorgenommen. Eine Vererbung von Eigenschaften von einer Menge zur anderen tritt nur implizit über eine Enthaltensbeziehung auf. Es tritt nur eine Sorte von Quantoren auf. Auch sei angemerkt, dass außer der Negation kein weiterer aussagenlogischer Operator auftritt.

21. In dem Blogeintrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 21 geht es um die Interpretation der Muster 3-4 der Schlussfigur 1. Dabei entsteht die Vermutung, dass viele der Unterscheidungen von Avicenna (die weitgehend auf Aristoteles zurückgehen!) möglicherweise ‚redundant‘ sind, d.h. mit anderen Formulierungen letztlich doch ‚das Gleiche‘ sagen. Der Ansatzpunkt für diese Vermutung liegt darin begründet, dass die Unterscheidung von einem Term als ‚Subjekt‘ (S) und als ‚Prädikat‘ (P) auf Seiten der abstrakten Bedeutungsstruktur als Bedeutungsrepräsentation jeweils ein ‚echtes‘ oder ein ‚unechtes‘ Objekt haben können, und zwar so, dass diese Strukturen ‚fließend‘ sind: jedes ‚echte‘ Objekt kann als ‚unechtes‘ interpretiert werden und umgekehrt. Weitere Vereinfachungen deuten sich an. Diese sollen im Folgenden überprüft werden.

Fortsetzung folgt …

QUELLEN

  • Avicenna, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
  • Digital Averroes Research Environment
  • Immanuel Kant, Critik der reinen Vernunft‘, Riga, 1781
  • Konrad Lorenz, 1973, ‚Die Rückseite des Spiegels. Versuch einer Naturgeschichte des menschlichen Erkennens‘, München, Zürich: Piper
  • Günther Patzig, ‚Die Aristotelische Syllogistik‘, 3,verb.Aufl., Göttingen: Vandenhoeck & Rupprecht, 1969
  • Nicholas Rescher (1928 – ),The Development of Arabic Logic. University of Pittsburgh Press, 1964
  • Hans-Jörg Sandkühler (Hg.) unter Mitwirkung von Dagmar Borchers, Arnim Regenbogen, Volker Schürmann und Pirmin Stekeler-Weithofer, ‚Enzyklopädie Philosophie‘, 3 Bd., Hamburg: FELIX MEINER VERLAG, 2010 (mit CD-ROM)
  • Stanford Encyclopedia of Philosophy, Aristotle’s Logic
  • Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7

Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER.

AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 7

Ausdruck, Ausdruck - einfacher, Ausdruck - sprachlicher, Ausdruck - zusammengesetzter, Avicenna, Bedeutung, Bedeutung eines Wortes, Bedeutungsbeziehung, Bedeutungsraum, Definition, Definition - explitite, Definition - rekursive, Definition - simultane, Logik, Logik - Alltag, Logik - Antike, Logik - formale, Modell, Objekt, Objekt - als Eigenschaft, Objekt - echtes, Objekthierarchie, Semantik, Struktur, Syntax

VORGESCHICHTE

1. In einem ersten Beitrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 1 hatte ich geschildert, wie ich zur Lektüre des Textes von Avicenna gekommen bin und wie der Text grob einzuordnen ist. In einem zweiten Beitrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 2 ging es um die Frage, warum überhaupt Logik? Avicenna führt erste Unterscheidungen zu verschiedenen Wissensformen ein, lässt aber alle Detailfragen noch weitgehend im Dunkeln. Im Teil AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 3 ging es um einfache und zusammengesetzte Begriffe, und bei den einfachen Begriffen um ‚individuelle‘ und ‚universelle‘. Schon hier zeigt sich der fundamentale Unterschied zwischen der antiken und der modernen-formalen Logik. In der antiken Logik wird die Ausdrucksebene E – und einer sich daran manifestierenden Folgerungslogik – immer in Verbindung mit einer zugehörigen Bedeutungsstruktur gesehen, die sich an einer Objektstruktur O festmacht. Die moderne formale Logik kennt zwar auch ‚Semantiken‘ und ‚Ontologien‘, diese sind aber ’sekundär‘, d.h. es werden nur solche ‚formalen Semantiken‘ betrachtet, die zum vorausgesetzten syntaktischen Folgerungsbegriff ‚passen‘. Dies sollte dann später an konkreten Beispielen diskutiert werden. Hier liegt der Fokus auf der antiken Logik im Sinne Avicennas. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 4 knüpft Avicenna an den zuvor eingeführten Begriff des ‚universellen‘ Begriffs an und betrachtet jetzt solche als ‚universell‘ bezeichneten Ausdrücke in einem Ausdruckskontext von aufeinanderfolgenden Ausdrücken. Alle diese Ausdrücke könnte man im Sinne der antiken Logik auch als ‚Urteile‘ bezeichnen, durch die einem bestimmten Ausdruck durch andere Ausdrücke bestimmte Bedeutungen (Eigenschaften) zu- oder abgesprochen werden. Hier unterscheidet er die Fälle eines ‚wesentlichen‘ Zusammenhanges zwischen zwei Begriffen und eines ’nicht wesentlichen‘ – sprich ‚akzidentellen‘ – Zusammenhangs. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 5 führt Avicenna eine Reihe von neuen technischen Begriffen ein, die sich nicht alle in ihrer Bedeutung widerspruchsfrei auflösen lassen. Es handelt sich um die Begriffe ‚Genus‘, ‚Spezies‘, Differenz, allgemeine und spezielle Akzidens, den Begriff ‚Kategorie(n)‘ mit den Kategorien ‚Substanz‘, ‚Qualität‘ und ‚Quantität‘. Die Rekonstruktion führt dennoch zu spannenden Themen, z.B. zu einem möglichen Einstieg in das weltverändernde Phänomen der kognitiven Evolution. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 6 geht es um die Begriffe ‚Definition‘ und ‚Beschreibung‘. Im Verhältnis zwischen beiden Begriffen geht die Beschreibung der Definition voraus. In der ‚Definition‘, die Avicenna vorstellt, wird ein neuer Ausdruck e mittels anderer Ausdrücke <e1, …, ek>, die sich auf schon bekannte Sachverhalte beziehen, ‚erklärt‘. Die von Avicenna dann vorgenommene Erklärung, was eine ‚Definition‘ sei, hängt u.a. stark ab von dem Begriff der ‚Bekanntheit‘ und dem Begriff des ‚wahren Wesens‘. Für die Tatsache, dass ein Mensch A bestimmte Ausdrücke <e1, …, ek> einer Sprache L ‚kennt‘ oder ’nicht kennt‘, dafür gibt es keine allgemeinen Regeln oder Kriterien. Von daher macht die Verwendung der Ausdrücke ‚bekannt’/ ’nicht bekannt‘ eigentlich nur Sinn in solch einem lokalen Kontexten W* (z.B. einem Artikel, ein Buch, ein Vortrag, …), in dem entscheidbar ist, ob ein bestimmter Ausdruck e einer Sprache L schon mal vorkam oder nicht. Schwierig wird es mit dem Begriff des ‚wahren Wesens‘. In meiner Interpretation mit der dynamischen Objekthierarchie gibt es ‚das wahre Wesen‘ in Form von Objekten auf einer Stufe j, die Instanzen auf Stufen kleiner als j haben. Dazu gab es weitere Überlegungen.

NAMEN, VERBEN/TERME, PRÄPOSITIONEN

2. Nach all den Vorüberlegungen nähert sich Avicenna nun dem eigentlichen Gegenstand der (antiken, auf das Alltagsdenken bezogenen) Logik, nämlich jenen ‚Ausdrücken‘, durch die entscheidende Bedeutungen kommuniziert werden.
3. Er beginnt mit ‚einfachen‘ Ausdrücken.

4. Er nimmt an, dass sich einfache Ausdrücke e aus drei Teilausdrücken zusammen setzen, die er als ‚Name‘, ‚Verb‘ und ‚Präposition‘ klassifiziert.

5. Terminologisch merkt er an, dass der grammatische Begriff ‚Verb‘ von Logikern ‚Term‘ genannt wird.

6. Sowohl der Name als auch das Verb sollen eine ‚vollständige Bedeutung‘ haben, Präpositionen dagegen nicht.

7. Namen unterscheiden sich von Termen dadurch, dass sie sich nicht auf eine ‚zeitliche Abfolge‘ (engl.: ‚temporal sequence‘) beziehen.

8. Verben hingegen – im Unterschied zu Namen – haben sowohl eine ‚Bedeutung‘ wie auch einen ‚zeitlichen Bezug‘ (engl.: ‚temporal significance‘).

9. Grenzfälle sind Namen wie ‚Heute‘ (engl.: ‚day‘) und ‚Gestern‘ (engl.: ‚yesterday). Obwohl sie einen ‚Teil der Zeit‘ (engl.: ‚part of time‘) bezeichnen (engl.: ’signify‘), sind sie doch keine Verben, da bei diesen Namen ihre ‚Bedeutung‘ mit dem ‚zeitlichen Bezug‘ zusammenfällt; bei einem Term wie ‚geschlagen‘ (engl.: ’struck‘) ist die Bedeutung (Vorgang des Schlagens) klar zu unterscheiden von dem Zeitbezug (der Vorgang war in der Vergangenheit).

10. Beispiele: e = <e1,e2,e3,e4,e5> = N:(Ich)Va:(habe)N:(den Zid)Vb:(gesehen); Der einfache Ausdruck e zerfällt in mehrere Ausdrucksteile <e1,e2,e3,e4,e5>, denen sich Bedeutungen zuordnen lassen. e1 = (Ich), bezieht sich auf den aktuellen Sprecher, und wird von daher als Name [N] für ein Objekt gewertet, das dem Namen eine Bedeutung verleiht. <e3, e4> = (den Zid) bezieht sich auf eine Person Zid, und wird auch als Name für ein Objekt gewertet, das dem Namen eine Bedeutung verleiht. e2 und e5 = (habe) … (gesehen) bezieht sich auf einen Vorgang des Sehens, bei der ein Beobachter etwas sieht (Bedeutungsanteil); zusätzlich wird ein zeitlicher Aspekt angedeutet, dass es sich um einen Vorgang in der Vergangenheit handelt. Ausdruck e1 füllt die ‚Rolle‘ des Beobachters und Ausdruck <e3, e4> spielt die Rolle des beobachteten Objekts.

11. Beispiel: e = <e1,e2,e3,e4> = N:(Zid) V:(ist) PRÄP:(im) N:(Haus). Der einfache Ausdruck e zerfällt in mehrere Ausdrucksteile <e1,e2,e3,e4>, denen sich Bedeutungen zuordnen lassen. e1 = N:(Zid) ist ein Ausdruck, der sich auf eine Person Zid bezieht, die dem Ausdruck als Objekt eine Bedeutung verleiht. e2 = V:(ist) ist ein Ausdruck, der sich auf einen Sachverhalt ‚etwas ist an einem Ort‘ bezieht, der dem Ausdruck sowohl eine Bedeutung verleiht wie auch eine davon unabhängige zeitliche Bestimmung, dass es in der Gegenwart ist. e3 = PRÄP:(im) ist ein Ausdruck, der sich auf einen räumlichen Sachverhalt bezieht ‚etwas ist in einem Raumgebiet‘, der dem Ausdruck eine Bedeutung verleiht, ohne expliziten Zeitbezug. e4 = N:(Haus) ist ein Ausdruck, der sich auf einen Ort Haus bezieht, der dem Ausdruck als Objekt eine Bedeutung verleiht. Die Kombination aus <e2, e3> ergibt einen Sachverhalt, der einerseits ein Objekt verlangt, von dem gesagt wird, dass es sich irgendwo befindet, und ein Objekt, das den Ort markiert. Beides ist mit e1 und e4 gegeben.

DISKUSSION

TERMINOLOGIE

12. Zur Terminologie: dass die (antiken) Logiker ‚Verben‘ als ‚Terme‘ bezeichnen sollen ist eine Sache. In diesem Kontext der Ausdrucksanalyse erscheint es mir eher verwirrend, zwei verschiedene Terminologien zu vermischen. Ich behalte im Folgenden die ‚grammatischen‘ Begriffe bei. Später kann man dann alle grammatischen Begriffe in einem mehr formalisierten logischen Kontext ‚übersetzen‘, falls notwendig.

13. Von ‚einfachen‘ Ausdrücken e zu sprechen, wenn die Ausdrücke sich alle aus mehreren Teilausdrücken e = <e1, e2, e3, …> zusammen setzen, kann verwirrend wirken, zumal er in vorausgehenden Abschnitten mit ‚einfachen‘ Ausdrücken tatsächlich solche meinte, die eben nicht zusammen gesetzt sind. Avicenna gibt keine direkte Erklärung für diese geänderte Verwendungsweise seines Begriffs eines ‚einfachen Ausdrucks‘, aber der Kontext legt folgende Interpretation nahe:

SYNTAX UND SEMANTIK

14. Es gibt eine ’syntaktische‘ Einfachheit (im Sinne von ’nicht zusammen gesetzt‘) und es gibt eine ’semantische‘ Einfachheit. Einfache Aussagen in diesem Abschnitt scheinen zu den ’semantisch einfachen‘ Ausdrücken zu gehören, denn syntaktisch sind sie eindeutig nicht einfach, sondern zusammengesetzt.

DER SEMANTISCHE RAUM

15. Damit stellt sich die Frage, wie man den ’semantischen Raum‘ ( den ‚Bedeutungsraum) eines Ausdrucks e (sowohl syntaktisch einfach als auch syntaktisch zusammengesetzt) so charakterisieren kann, dass man eine ‚einfache‘ Bedeutung von einer ’nicht einfachen = komplexen‘ Bedeutung unterscheiden kann.

16. Avicenna selbst hat ja in den vorausgehenden Abschnitten den ‚Bedeutungsraum‘ nicht ausdrücklich als eigenständigen Gegenstand thematisiert, immer nur indirekt, anhand von einzelnen Beispielen. Von diesen seinen indirekten, fragmentarischen Andeutungen aus lässt sich die Frage nach einer klaren Unterscheidung einer ‚einfachen‘ und einer ’nicht einfachen‘ Bedeutung im Kontext eines Ausdrucks e kaum einfach beantworten.

17. Als ‚Abfallprodukt‘ der bisherigen Rekonstruktion wurde das Konzept einer ‚dynamischen Objekthierarchie‘ O angedeutet, für die allgemeine Metaklassifikationen (entspricht in etwa dem klassischen Kategorienbegriff) wie z.B. ‚echtes Objekt‘ (etwa die Kategorie ‚Substanz‘), ‚unechte Objekte (etwa die Kategorie ‚Qualität‘), ‚Zeit‘, ‚Raum‘ und ‚Zahl‘ (etwa die Kategorie ‚Quantität‘) postuliert werden konnten.

18. Wenn man nun also von einem ‚Bedeutungsraum‘ (semantischen Raum) M sprechen will, dann müsste man entweder diese – bislang nur angedeuteten – Objektstrukturen mit den zusätzlichen Metaklassifikationen zugrunde legen oder eine Alternative formulieren. Ohne irgendwelche Annahmen dieser Art wäre der Begriff des semantischen Raumes vollständig leer und damit jegliche Art von Rekonstruktion von Ausdrücken e mit Bezug auf die zugehörigen ‚Bedeutungen‘ beliebig: alles wäre richtig und zugleich falsch.

19. Bis auf weiteres wird hier die bisherige Skizze zum dynamischen Objektraum mit den Metaklassifikationen als Arbeitshypothese für die weitere Interpretationen benutzt.

20. Von einem Ausdruck e mit Teilausdrücken <e1, e2, e3, …> zu sagen, dass bestimmte Ausdrucksteile $latex e_{i}$ bestimmte, voneinander abgrenzbare Bedeutungen haben, ihnen also unterschiedliche ’semantische Funktionen‘ zukommen, ist einerseits gewagt, da die Ausrücke als solche keinerlei syntaktische Hinweise haben müssen, aus denen man dies erkennen könnte, zugleich aber auch interessant, da damit die Denkaufgabe gestellt wird, wie es möglich sein soll, beliebige Ausdrucksteile $latex e_{i}$ in einem Ausdruck e durch Bezugnahme auf ‚etwas anderes‘, nämlich auf die ‚Bedeutung‘ indirekt charakterisieren zu können.

SIMULTANE DEFINITONEN

21. In gewissem Sinne könnte man hier auch von einem Definitionsvorgang sprechen: das Neue, das Unbekannte, das sind die Ausdruckselemente <e1, e2, e3, …> in einem Ausdruck e, das Bekannte das ist ein vorausgesetztes Bedeutungsgefüge, und die definitorische Erklärung ist die Verbindung von neuem Ausdruckselement und bekanntem Bedeutungsobjekt. Abweichend vom einfache Fall der expliziten syntaktischen Definition von einem Element e durch eine Folge von anderen Ausdrücken <e1, e2, e3, …> haben wir es hier im Falle der Definition von syntaktischen Ausdrücken durch Bezugnahme auf semantische Objekte mit zwei zusätzlichen Aspekten zu tun: (i) die Erklärung findet nicht in ein und demselben syntaktischen Raum statt sondern es werden zwei ansonsten getrennte Räume miteinander verknüpft: der syntaktische Raum mit dem semantischen Raum, und umgekehrt. Ferner (ii) wird nicht nur ein einziges syntaktisches Element ‚erklärt‘, sondern es werden mehrere syntaktische Elemente ‚parallel’/ ’simultan‘ erklärt.

22. Einen vergleichbaren Fall von ’simultaner‘ Erklärung haben wir im Falle von mathematischen Strukturtheorien, wie sie auch bei modernen empirischen Theorien auftreten. Ein typischer Fall wäre eine Struktur wie $latex < M, f1, …, fk >$. Hier werden mehrere Ausruckselemente eingeführt, deren Bedeutung sich erst im (syntaktischen) Gesamtkontext ergibt, der zusätzlich mit semantischen Elementen aufgeladen werden kann.

23. Ein anderes Beispiel sind formale Semantiktheorien, in denen zusammengesetzte Ausdrücke der Art e = <e1, e2, …> durch eine komplexe Abbildungsvorschrift so auf eine formale Struktur (auch ‚Domäne‘ oder ‚Modell‘ genannt) bezogen werden, dass für jeden syntaktisch zusammengesetzten Ausdruck e gesagt werden kann, wann das ‚Modell‘ M diese syntaktischen Ausdrücke ‚erfüllt‘, oft geschrieben $latex M \models e$ mit ‚e‘ als dem Ausdruck, der durch das Modell ‚erfüllt‘ wird.

24. Eine Besonderheit bei diesen Charakterisierungen von Ausdruckselementen e über den ‚Umweg‘ einer Bedeutungsstruktur M liegt darin, dass es nicht ausreicht, jedem einzelnen Teilausdruck $latex e_{i}$ eine – quasi isolierte – Bedeutung zuzuordnen, sondern die einzelnen bedeutungsfundierenden Objekte O der Bedeutungsstruktur M kommen in bedeutungsspezifischen Anordnungen (in Raum, Zeit, …) vor. Diese spezifischen Sachverhalte müssen in den Ausdruckselementen mitkodiert werden. Es reicht also nicht, nur zu sagen, dass das Ausdruckselement ‚e1‘ ein Objekt o1 bezeichnet, das für eine konkrete Person steht, sondern man muss zusätzlich auch – meistens – einen möglichen ‚Vorgang‘ benennen, in den das Objekt o1 eingebettet ist, und – meistens – zusätzlich mit einem zeitlichen Aspekt. Das wären dann schon mindestens drei verschiedene Kodierungsdimensionen, die im Bereich der Ausdruckselemente repräsentiert werden müssten.

25. Aufgrund der Beispiele von Avicenna gäbe es die zusätzlichen Arbeitshypothesen, dass (i) Vorgänge durch ‚Verben‘ [V] kodiert werden, (ii) zeitliche Aspekte sowohl durch Verben wie auch durch ‚Namen‘ [N], und (iii) räumliche Aspekte durch ‚Präpositionen‘ [PRÄP].

26. Die interessante Frage wäre natürlich, wie genau diese verschiedenen Objektstrukturen und -eigenschaften und -Relationen in der dynamischen Objekthierarchie O als dem Bedeutungsraum M repräsentiert sind. Sie müssten ja so vorliegen, dass man sie einfach ‚ablesen‘ könnte und dann durch einen entsprechenden ‚Übersetzungsprozeß‘ von M nach E zugeordnet werden könnten, also $latex \lambda: M \longrightarrow E$ (mit $latex \lambda $ als Übersetzungsvorschrift).

27. Nehmen wir das Beispiel e = <e1,e2,e3,e4> = N:(Zid) V:(ist) PRÄP:(im) N:(Haus). Es gibt hier (woher wissen wir dies überhaupt!) zwei Ausdruckselemente e1 und e4, die sich auf ‚echte Objekte‘ beziehen; e1 bezieht sich auf eine konkrete Personen, e4 auf ein Objekt, in dem Menschen sich aufhalten können. Der Ausdruck ist kein echtes Objekt, da es nur eine bestimmte Form von Beziehung zwischen zwei Objekten repräsentiert, nämlich dass ein Objekt A ‚räumlich in‘ einem anderen Objekt B vorkommt. Das Ausdruckselement e2 repräsentiert einen Zusammenhang zwischen zwei Objekten (echt oder unecht), der zudem aktuell ist, genauer: von einem Zielobjekt A wird gesagt, dass es in einer ist-Beziehung zu einem anderen Objekt steht. Da aber nach dem ‚Sprachgefühl‘ (was ist das?) die Kombination <e1, e2, e4> nicht geht, muss also <e3,e4> zusammen auftreten, damit e1 mittels e2 mit e4 kombiniert werden kann. Eine Arbeitshypothese könnte sein, dass echte Objekte, die mögliche ‚Orte des Vorkommens‘ bezeichnen, eine zusätzliche Präposition benötigen, um als Gegenpart in einer ist-Relation auf zu treten. Das ist natürlich hier alles sehr ad hoc und unsystematisch. Es kann aber verdeutlichen, dass die große Arbeitshypothese mit der bereichsübergreifenden Zuordnung $latex \lambda $ von Elementen einer Bedeutungsstruktur M (mit der dynamischen Objekthierarchie O als Teilstruktur) zu einer Menge E von möglichen Ausdrücken eine sehr detaillierte Beschreibung verlangt, die nicht ad hoc entscheidet, sondern systematisch.

Eine Fortsetzung zu diesem Beitrag findet sich HIER.

QUELLEN

  • Avicenna, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
  • Digital Averroes Research Environment
  • Stanford Encyclopedia of Philosophy, Aristotle’s Logic
  • Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7

Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER.

AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 4

Avicenna, Bedeutung, Bedeutung - abstraktes Konstrukt, Bedeutung - akzidentell, Bedeutung - kontingent, Bedeutung - wesentliche, Bedeutung eines Wortes, Bedeutungsbeziehung, Bedeutungsmaterial, Logik, Logik - Alltag, Logik - Antike, Logik - formale, Metaphysik, Objekt, Objekt - als Eigenschaft, Objekt - echtes, Objekt - kontingent, Objekt - universell, Objekttyp, Ontologie

VORGESCHICHTE

1. In einem ersten Beitrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 1 hatte ich geschildert, wie ich zur Lektüre des Textes von Avicenna gekommen bin und wie der Text grob einzuordnen ist.
2. In einem zweiten Beitrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 2 ging es um die Frage, warum überhaupt Logik? Avicenna führt erste Unterscheidungen zu verschiedenen Wissensformen ein, lässt aber alle Detailfragen noch weitgehend im Dunkeln.
3. Im Teil AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 3 ging es um einfache und zusammengesetzte Begriffe, und bei den einfachen Begriffen um ‚individuelle‘ und ‚universelle‘. Schon hier zeigt sich der fundamentale Unterschied zwischen der antiken und der modernen-formalen Logik. In der antiken Logik wird die Ausdrucksebene E – und einer sich daran manifestierenden Folgerungslogik – immer in Verbindung mit einer zugehörigen Bedeutungsstruktur gesehen, die sich an einer Objektstruktur O festmacht. Die moderne formale Logik kennt zwar auch ‚Semantiken‘ und ‚Ontologien‘, diese sind aber ’sekundär‘, d.h. es werden nur solche ‚formalen Semantiken‘ betrachtet, die zum vorausgesetzten syntaktischen Folgerungsbegriff ‚passen‘. Dies sollte dann später an konkreten Beispielen diskutiert werden. Hier liegt der Fokus auf der antiken Logik im Sinne Avicennas.

WESENTLICHE UND NICHT-WESENTLICH (AKZIDENTIELL, KONTINGENT…)

4. Im nächsten Abschnitt knüpft Avicenna an den zuvor eingeführten Begriff des ‚universellen‘ Begriffs an, das sind jene, die zwar eine Bedeutung haben, diese Bedeutung kann aber verschiedene konkreten ‚Instanzen‘, ‚Realisierungen‘, ‚Beispiele‘ umfassen (also: der Ausdruck ‚Tasse‘ kann sich auf viele verschiedene konkrete Tassenobjekte beziehen).
5. Er betrachtet jetzt solche als ‚universell‘ bezeichneten Ausdrücke in einem Ausdruckskontext von aufeinanderfolgenden Ausdrücken mit den folgende Kombinationen von Ausdrücken (hier in deutscher Übersetzung): (i) ‚Der Mensch ist ein Lebewesen‘, (ii) ‚Vier ist eine Zahl‘, (iii) ‚Der Mensch existiert‘, (iv) ‚Zahlen existieren‘, (v) ‚Der Mensch ist weiß‘, (vi) ‚Der Mensch ist nicht weiß‘, (vii) ‚Der Mensch lacht‘, (viii) ‚Zid sitzt‘, (ix) ‚Zid schläft‘, (x) ‚Zid ist alt‘, (xi) ‚Zid ist jung‘.
6. Alle diese Ausdrücke könnte man im Sinne der antiken Logik auch als ‚Urteile‘ bezeichnen, durch die einem bestimmten Ausdruck durch andere Ausdrücke bestimmte Bedeutungen (Eigenschaften) zu- oder abgesprochen werden (z.B. wird in (v) dem Objekt (der Mensch) die Eigenschaft (weiß) zugesprochen).
7. Er nimmt folgende interessante Unterscheidung vor: (i) er betrachtet sowohl ‚universelle‘ Ausdrücke wie ‚Mensch‘, ‚Zahl‘, ‚Lebewesen‘, Vier‘ und einen ‚individuellen‘ Ausdruck wie ‚Zid‘ als Bezeichnung eines konkreten Objektes, das als Instanz eines ‚Menschen‘ genommen wird, und (ii) sagt dann, dass die Bedeutung (‚meaning‘) dieser Ausdrücke sich aus dem ‚Wesen‘ des Objektes ergibt. D.h. dasjenige, was wir aufgrund unserer sinnlichen Wahrnehmung in Verbindung mit unseren Denkprinzipien als Objekt ‚Mensch‘ oder ‚Vier‘ oder ‚Zahl‘ oder ‚Zid‘ abstrahierend erkennen können, das ergibt sich nicht einfach so, nicht zufällig, nicht kontingent, nicht akzidentiell, sondern dies ergibt sich aus dem ‚Wesen‘ des Objektes, und zwar notwendig, zwingend, eben ‚essentiell‘, ‚wesenhaft‘.
8. In der Ausdrucksfolge (Der Mensch) (ist) (weiß) wird eine Beziehung zwischen der Bedeutung des Ausdrucks (der Mensch) und (weiß) durch Verwendung des Ausdrucks (ist) hergestellt. In der ’normalen Verwendung‘ bedeutet dies, dass die Bedeutung von (weiß) der Bedeutung von (der Mensch) zugesprochen wird.
9. Doch aus der Kenntnis der Bedeutung des Ausdrucks (der Mensch) folgt nach Avicenna nicht notwendigerweise die Kenntnis der Bedeutung des Ausdrucks (weiß) als Teil von (der Mensch). Die Begründung von Avicenna: zum ‚Wesen‘ des Menschen gehört es nicht, dass er ‚weiß‘ ist; er kann ‚weiß‘ sein, aber er muss nicht.
10. Das ist die entscheidende Argumentationsfigur: charakteristisch für ‚wesentliche‘ Ausdrücke ist es, dass deren Bedeutung sich auf Objekte bezieht, denen aufgrund ihres ‚Wesens‘ bestimmte Eigenschaften notwendig zukommen, andere aber nicht.
11. Doch lassen die Sätze von Avicenna noch eine weitere Deutung zu. Im Fall von ‚universellen‘ Ausdrücken unterscheidet er ja die universelle (eine) Bedeutung von den möglichen ‚Instanzen‘ (in der englischen Übersetzung wird ‚Instanz‘ als ein ‚particular‘ bezeichnet). Die Frage ist, ob und inwieweit sich die Eigenschaften der universellen Bedeutung auf die Instanzen überträgt.
12. Hier benutzt Avicenna zwei Gedanken: (i) Er sagt, dass die ‚Existenz‘ der universellen Bedeutung die Voraussetzung (‚prerequisite‘) für die ‚Existenz‘ der besonderen Bedeutung ist und (ii) dass die besondere Bedeutung aus der universellen Bedeutung folgt.
13. Also, wenn der Ausdruck (der Mensch) (ist) (ein Lebewesen) Sinn machen soll, dann muss die allgemeine Bedeutung von ‚Lebewesen‘ gegeben sein und es muss klar sein, dass ‚Mensch‘ eine Instanz (in der englischen Übersetzung ein ‚particular‘) von der allgemeinen (wesentlichen) Bedeutung ‚Lebewesen‘ ist; entsprechend setzt der Name ‚Zid‘ die Existenz der allgemeinen Bedeutung von ‚Mensch‘ voraus.
14. Interessant ist noch das Detail, dass Avicenna die ‚Seele‘ als wesentlich zur Bedeutung von ‚Mensch‘ gehörig ansieht. Bedenkt man, wie schwierig (bis unmöglich?) es ist, die Bedeutung von ‚Seele‘ zu klären, kann es zumindest verwundern, wie apodiktisch er behaupten kann, dass die ‚Seele‘ eine wesentliche Eigenschaft der Bedeutung (und damit des Objektes) ‚Mensch‘ sei.

DISKUSSION

15. Mit diesem Abschnitt über ‚wesentliche‘ und ’nicht wesentliche‘ gleich ‚akzidentiellen‘ / ‚kontingenten‘ / ‚arbiträren‘ Eigenschaften eines Bedeutungsobjektes O sind wir schon in den tiefsten Abgründen einer Ontologie bzw. einer Metaphysik gelandet.
16. Dazu muss man sich nochmals bewusst machen, dass die Ausdrücke E (die selbst sinnliche Muster der Wahrnehmung sind und die auch Abstraktionsprozessen unterliegen; man denke nur an die ‚type’/ ‚token‘ Unterscheidung der Linguisten) in Beziehung gesetzt werden zu Bedeutungselementen, die gegeben sind als aus der sinnlichen Wahrnehmung $latex K_{s}$ abstrahierte Objekte O, die in verschiedenen Abstraktionsstufen organisiert sind. Alle (!) diese Objekte setzen Wahrnehmungsprozesse voraus, die mit einer elementaren Form von Lernen verknüpft sind.
17. Wenn also ein Mensch A zu einem bestimmten Zeitpunkt t durch seine individuellen Lernprozesse in einer bestimmten Sprachgemeinschaft mit Sprache L ‚gelernt‘ hat, dass ein Ausdruck e sich mit bestimmten – aus der Wahrnehmung gewonnenen – Objekten O verbindet – als m(o,e) –, dann kann man folgende Unterscheidung treffen: (i) sofern sich diese Wahrnehmungsobjekte O auf Eigenschaften der umgebenden Welt W beziehen, die im Zeitraum des Lernens von Mensch A mehr oder weniger ‚konstant‘ / ‚unveränderlich‘ waren, dann ‚existiert‘ die ‚erlernte Bedeutung‘ O für den Menschen A und die gelernten Bestandteile von O sind für diesen Menschen A ‚wesentlich‘; ebenso für alle anderen Menschen, die mit diesem Aspekt der umgebenden Welt W in Berührung gekommen sind. Wenn (ii) die gelernten Eigenschaften O der umgebenden Welt aber ‚variabel‘ sind, mal so und mal so, also akzidentiell/ kontingent/ arbiträr, dann ‚kennt‘ der lernende Mensch A zwar diese möglichen Bedeutungen O‘, sie aber mit einem anderen Objekt O in Verbindung zu bringen, ist nicht notwendig, ist nicht zwingend, sondern muss sich aus der aktuellen kontingenten Situation ‚ergeben‘. Wenn üblicherweise ein Mensch nicht weiß ist (weil alle anderen in der Umgebung schwarz sind), dann wäre das Ereignis, dass ein Mensch auftritt, der weiß ist, ein ‚interessantes‘ Ereignis, das zu berichten lohnen würde.
18. Ein Mensch B mit einer anderen Sprache L‘ wird die Ausdrücke der Sprache L von Mensch A zunächst nicht verstehen (z.B. sei L= Arabisch und L’=Hebräisch). Wenn aber der Mensch A sich auf einen Aspekt X der umgebenden Welt W bezieht, den auch der Mensch B wahrnehmen kann, dann haben A und B die leise Chance, aufgrund der gemeinsamen Kenntnisnahme von X die hinreichend ‚gleichen Wahrnehmungen O(X)‘ zu haben, und dann kann B eventuell ‚begreifen‘, dass der arabische Ausdruck von A sich auf dieses gemeinsam wahrnehmbare O(X) bezieht, und er dann aufgrund seiner Kenntnis des L’=Hebräischen weiß, wie er den L= arabischen Ausdruck für O(X) im Hebräischen wiedergeben würde.
19. Wichtig ist hier, dass die ‚Existenz‘ einer Bedeutung O(X) generell von ‚existierenden Eigenschaften X in der umgebenden Welt W‘ abhängt UND (!!!) von den daran anknüpfenden Wahrnehmungsprozessen, die – stimuliert von X – zu den entsprechenden Bedeutungsobjekten O(X) führen. Existieren in diesem Sinne Bedeutungen O(X), dann kann man von ihren Eigenschaften sagen, dass sie ‚wesentlich‘ sind, wenn sie ’normalerweise immer‘ so vorkommen.
20. Solange man sich der sinnlichen Herkunft aller Bedeutungen bewusst ist, solange hat man auch keine Probleme damit, dass ‚Menschen‘ aufgrund ihrer genetischen Basis im Laufe der Zeiten zu ganz unterschiedlichen Erscheinungsweisen kommen können: verschiedene Hautfarben, verschiedene Körperformen, verschiedene Deformationen (keine Arme, verkrüppelte Beine, anders geformte Köpfe, …), unterschiedliche Intelligenzen, usw. Heute zusätzlich erweitert durch medizinische Operationen, Schönheitsoperationen, allerlei Prothesen und Implantate. Dass der Begriff ‚Mensch‘ vor diesem Hintergrund unterschiedliche Bedeutungen O aufgrund unterschiedlicher Gegebenheiten X in der Welt annehmen kann, sollte dann kein Problem sein.
21. Schwieriger wird es, wenn man – was in der Vergangenheit ständig geschah – glaubte, aus den empirisch gewonnenen Bedeutungen O(X) auf ‚allgemeine Strukturen‘ schließen zu können, die ‚hinter‘ den empirischen Eigenschaften in dem Sinne liegen, dass sie den empirischen Ereignissen ‚zeitlich und logisch vorausgehen‘. In diesen Zusammenhang gehört der populäre Geist-Materie-Dualismus, nach dem die materiellen Erscheinungen ‚Ausfluss‘ geistiger Strukturen sind, die als solche die ‚wesentlichen‘ Eigenschaften repräsentieren.
22. Psychologisch sind solche Denkfiguren verständlich, da sich die Antike auch die Frage gestellt hat, wie die vielfältigen empirischen Formen der umgebenden Welt trotz allem nicht ganz arbiträr sind, sondern offensichtlich gewissen ‚Regeln‘ / ‚Gesetzen‘ folgen. In Unkenntnis der modernen Physik und Biologie konnte man nur sehr allgemeine Annahmen machen, meist sehr statische. Heute beginnen wir zu verstehen, dass die Vielfalt der Formen auf spezifische Erzeugungsprozesse zurückgehen, die wiederum allgemeinen Gesetzen folgen. Diese Gesetze erlauben in der Umsetzung viel Variabilität, so dass Vielfalt und Regelhaftigkeit keinen Widerspruch darstellen.
23. Die Kernaussagen von Avicenna zu der Begriffslogik bis zu dieser Stelle kann man aber wohl aufrecht erhalten. Erst wenn man aufgrund von Erfahrungen anlässlich X Bedeutungen O(X) ausbilden konnte kann man mit diesen Bedeutungen Urteile der Art bilden ‚Etwas X existiert‘ oder ‚Ein Etwas X ist ein Etwas Y‘.
24. Wichtig ist hier aber, zu sehen, dass das ‚Denknotwendige‘ der Alltagslogik sich nicht aus den Ausdrücken E als solchen ergibt, sondern aus den Eigenschaften der mit den Ausdrücken verknüpften Bedeutungen O(X).
25. Bislang wurde hier nur angenommen, dass die Bedeutungsobjekte O ‚Hierarchien‘ bilden können. Dies erklärt, wieso eine Bedeutung ‚universell‘ sein kann im Sinne von Allgemeinbegriff – Instanzen. Im Fall von (Zid) (ist) (ein Mensch) wäre ‚Zid‘ eine Instanz von Mensch; oder im Fall von (Der Mensch) (ist) (ein Lebewesen) wäre (der Mensch) eine Instanz von (Lebewesen). Entsprechend wäre (Zid) (schläft) ein Urteil, in dem von Zid (als Instanz von Mensch) gesagt würde, er habe die Eigenschaft zu schlafen. Sofern man ’schlafen‘ als ‚typisch‘ für Menschen ansehen würde, wäre dies eine ‚wesentliche‘ Aussage, da es normalerweise so ist. Würde man sagen, der Mensch schläft nur gelegentlich, dann wäre es eine akzidentelle/ kontingente Eigenschaft, eben nicht wesentlich.
26. Diese Beispiele mit (ist)(weiß), (schläft), (sitzt) legen den Schluss nahe, dass die Bedeutung O(X) nicht nur ein gleichförmiges Etwas ist, sondern aus einer Menge von ‚unterscheidbaren Eigenschaften‘ [PROP] bestehen kann.
27. Daraus würde folgen, das z.B. die Instanz ‚Zid‘ und die Instanz ‚Hans‘ von der Bedeutung ‚Mensch‘ jeweils bestimmte Eigenschaften PROP_Hans und PROP_Zid aufweisen, die so sind, dass der Oberbegriff ‚Mensch‘ solche Eigenschaften PRP_Mensch aufweist, die sowohl Zid und Hans gemeinsamen haben; Zid und Hans können aber auch Eigenschaften aufweisen, die sie voneinander unterscheiden und die nicht in im universellen Begriff ‚Mensch‘ vorkommen.
28. Also $latex PROP_{Mensch} = PROP_{Zid} \cap PROP_{Hans}$ würde sowohl die Menge der gemeinsamen Eigenschaften der beiden Instanzen ‚Zid‘ und ‚Hans‘ bezeichnen als auch die Verbindung zwischen dem universellem Begriff und seinen Instanzen herstellen.
29. Stellt sich noch die Frage, was denn dann die ‚Eigenschaften‘ sind? Setzen wir den bisherigen Zusammenhang voraus, dann haben wir die Annahme einer umgebenden Welt W mit ‚Welteigenschaften‘ X und einen Menschen als ein System, das mittels seiner Sinnesorgane eine Wahrnehmung (‚perception‘) als Abbildung von bestimmten dieser Welteigenschaften X auf innere sensorische Muster $latex K_{s}$ realisieren kann ($latex perc: X \longrightarrow K_{s}$). Aus diesen Mustern $latex K_{s}$ lassen sich dann mittels Abstraktion unterschiedlichste Objekte O generieren ($latex \alpha: K_{s} \cup K_{p} \longrightarrow O$) (unterstellt, dass dabei implizite Denkprinzipien $latex K_{p}$ nach Avicenna mitwirken können (was nahezu alle Philosophen ähnlich angenommen haben)). Aus diesen Annahmen ergibt sich, dass jedwede Eigenschaft auch solch ein abstrahiertes Objekt aufgrund von Sinneseindrücken sein muss.
30. Fragt sich dann, ob sich Objekte und Eigenschaften von Objekten unterscheiden, und wie?
31. Intuitiv würde man sagen: Ja. Aber wie genau?
32. Hier könnte man Avicennas Begriffe ‚universell‘ und ‚wesentlich‘ bemühen: ein ‚echtes‘ Objekt umfasst andere Objekte (als Eigenschaften), die ihm ‚wesentlich‘ zukommen, d.h. ’normalerweise‘, ‚regelhaft‘; ein ‚unechtes‘ Objekt ist ein solches, das zwar als ‚Teil von einem echten Objekt‘ auftreten kann, normalerweise aber nicht alleine vorkommt. So wäre eine ‚Rose‘ tendenziell ein ‚echtes Objekt‘, da es mit bestimmten Eigenschaften ’normalerweise‘ auftritt, ‚Rot‘ wäre aber ein ‚unechtes‘ Objekt, da ‚Rot‘ normalerweise nicht isoliert auftritt sondern nur in Verbindung mit anderen Objekten; z.B. kann das Objekt ‚Rose‘ das Objekt ‚Rot‘ als Eigenschaft – also als unechtes Objekt – enthalten.
33. Die Unterscheidung von (echtem) Objekt und (unechtem) Objekt (als Eigenschaft) hängt damit von der ‚gelernten‘ Bedeutung ab: was tritt wann wie oft und welcher Konstellation auf.
34. ‚Wesentlich‘ wird hier interpretiert als ‚regelmäßige Erscheinung‘ (normal), und ’nicht wesentlich‘ bzw. kontingent bzw. akzidentell wird hier interpretiert als ’nicht regelmäßig‘, ’nicht normal‘, ‚gelegentlich‘, ‚zufällig‘ auftretend.

Fortsetzung folgt …

QUELLEN

  • Avicenna, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
  • Digital Averroes Research Environment
  • Stanford Encyclopedia of Philosophy, Aristotle’s Logic
  • Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7

Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER.

AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 3

Ausdruck, Ausdruck - einfacher, Ausdruck - sprachlicher, Ausdruck - zusammengesetzter, Avicenna, Bedeutung, Bedeutung - abstraktes Konstrukt, Bedeutung eines Wortes, Bedeutungsbeziehung, Bedeutungskorrelat, individuell, Logik, Logik - Antike, Objekt, universell

VORGESCHICHTE

1. In einem ersten Beitrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 1 hatte ich geschildert, wie ich zur Lektüre des Textes von Avicenna gekommen bin und wie der Text grob einzuordnen ist.
2. In einem zweiten Beitrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 2 ging es um die Frage, warum überhaupt Logik? Avicenna führt erste Unterscheidungen zu verschiedenen Wissensformen ein, lässt aber alle Detailfragen noch weitgehend im Dunkeln.
In diesem Teil geht es jetzt um einfache und zusammengesetzte Begriffe.

AUSDRÜCKE: EINFACH UND ZUSAMMENGESETZT

3. In Weiterführung seiner Redeweise von sprachlich vermitteltem Wissen $latex K_{m}$ verstanden als ein Paar bestehend aus einem Bündel von sinnlichen Eindrücken $latex k \subseteq K_{s}$ einerseits und einem Ausdruck $latex e \in E, E \subseteq K_{s}$ andererseits, also m(k,e), führt er jetzt die Unterscheidung von ‚einfachen‘ und ‚zusammengesetzten‘ Ausdrücken ein. Der Ausdruck ‚einfach‘ bezieht sich dabei auf die Menge der ‚Bedeutungsbeziehungen‘, in denen ein Ausdruck e vorkommt. Kommt der Ausdruck e nur in einer Bedeutungsbeziehung vor, also m(k,e), dann ist er einfach. Kann man aber einen Ausdruck e zerlegen, so dass einzelnen Teilen $latex e_{i}$ jeweils eine eigene Bedeutungsbeziehung zugewiesen werden kann, dann ist er ‚zusammengesetzt‘, also etwa $latex e = \langle e_{1}, …, e_{n} \rangle$ mit $latex m_{1}(k_{1}, e_{1}), … m_{n}(k_{n}, e_{n})$.

EINFACHE AUSDRÜCKE: INDIVIDUELL ODER UNIVERSELL

4. Avicenna führt dann noch die weitere Unterscheidung ein, dass ‚einfache Ausdrücke‘ entweder ‚individuell‘ sein können oder ‚universell‘.

5. Er motiviert diese neuen Begriffe so, dass er sagt, dass ein einfacher Ausdruck e mit m(k,e) nur eine einzige Entität (‚entity‘) bezeichne, wohingegen ein einfacher Ausdruck m(k*,e), der als ‚universell‘ gilt, mit seiner Bedeutungskomponente ‚k*‘ viele Entitäten (‚many entities‘) bezeichne.

DISKUSSION

6. So einfach diese neuen Begriffe ‚einfach/ zusammengesetzt‘ sowie bei ‚einfach zusätzlich ‚individuell/ universell‘ klingen, so stehen sie für ein Geflecht von Problemen, das dies heute nicht als gelöst gelten kann.

7. Wie schon in der Diskussion von Teil 2 deutlich wurde, setzt die Diskussion der Unterscheidung der verschiedenen Wissensformen einen begrifflichen Rahmen voraus, der letztlich auf generelle Annahmen zum erkennen Subjekt hinausläuft, wie es etwa im Rahmen einer Erkenntnistheorie geleistet werden könnte, also ein abstraktes Modell eines erkennenden Subjektes, das den formalen Rahmen liefert, innerhalb dessen dann über spezielle Sachverhalte wie ’sprachliches‘ oder ‚logisches‘ Wissen gesprochen werden kann.

8. Schon die Einführung der Unterscheidung von sprachlichen Ausdrücken $latex E \subseteq K_{s}$, die in einer ‚Bedeutungsbeziehung‘ M zu anderen sinnlichen Ereignissen $latex K_{s} \subseteq K$ stehen, können als $latex M \subseteq K_{s} \times E$, wirft eigentlich zusätzliche Fragen auf, die bislang von Avicenna nicht geklärt wurden.

9. Nun zu sagen, dass ein einfacher Ausdruck e in genau einer Bedeutungsbeziehung m stehe, und die darin vorkommenden sinnlichen Ereignisse k genau ‚eine Entität‘ bezeichnen, legt die Vorstellung nahe, dass bestimmten Mustern sinnlicher Ereignisse k etwas ‚Abstrakteres‘ korrespondiert, nämlich ein ‚Objekt‘ o mit $latex o \in O$. Daraus würde folgen, dass die Bedeutungsbeziehung möglicherweise nicht direkt auf Muster k von sinnlichen Ereignissen abzielt, sondern auf abstrakte Objekte O, die aus den sinnlichen Mustern k durch einen Abstraktionsprozess $latex \alpha$ erzeugt werden; also $latex \alpha: KS \longrightarrow O$ und $latex M \subseteq O \times E$.

10. Nimmt man diese Interpretation an, dann ließe sich der Fall von ‚einfachen‘ Ausdrücken, die bedeutungsmäßig ‚universell‘ sind, so rekonstruieren, dass sich im Bereich der abstrakten Objekte O mehr als eine ‚Abstraktionsebene‘ denken lässt. Analog der Whitehead-Russelschen Typentheorie aus den Principia Mathematica gibt es dann Abstraktionsebenen von 1 bis n, und ein Objekt auf der Ebene j könnte alle Objekte von Abstraktionsebenen ‚kleiner als j‘ als ‚Instanzen‘ haben.

11. Dazu müsste man die Abstraktionsfunktion ein wenig verallgemeinern zu $latex \alpha: KS \cup O \longrightarrow O$, und man müsste sich noch die Hierarchie der Ebenen ‚dazudenken‘.

12. Beispiel: auf dem Tisch stehen verschiedene konkrete, einzelne Tassen $latex \{ t_{1}, …, t_{r} \}$; diese repräsentieren einzelne Entitäten (Ebene 1). Dazu gibt es den abstrakteren Begriff ‚Tasse‘ auf einer Ebenen 2. Auf dem Tisch befinden sich aber auch noch andere Gegenstände, z.B. ‚Teller‘, ‚Bestecke‘ usw. Die Begriffe ‚Teller‘ und ‚Besteck‘ bezeichnen Objekte der Ebene 2. Man könnte jetzt von diesen unterschiedlichen Objektarten weiter ‚abstrahieren‘ und z.B. den Begriff ‚Frühstücksgegenstände‘ auf Ebene 3 einführen. Die konkreten Tassen sind Instanzen des Begriffs ‚Tasse‘; die Begriffe ‚Tasse‘, ‚Teller‘, ‚Besteck‘ sind Instanzen von ‚Frühstücksgegenstände‘; es könnten aber auch natürlich die konkreten Tassen, konkreten Bestecke usw. als Instanzen des Begriffs ‚Frühstücksgegenstände‘ bezeichnet werden.

13. Dies würde bedeuten, dass man einem Ausdruck e zwar genau ‚eine Bedeutung‘ o zuordnen kann, diese Bedeutung o gehört aber zu einer Hierarchie von ‚Objekten‘ O, die, je nach Stellung in der Hierarchie der Bedeutungsobjekte, unterschiedliche andere Objekte von einer ’niedrigeren‘ Stufe/ Ebene‘ als ‚Instanzen‘ beinhalten kann. Dies führt dazu, dass man neben den bisherigen Unterscheidungen von Wissensformen noch eine weitere einführen müsste, nämlich das ‚Objektwissen‘ $latex K_{o}$, das eine Objekthierarchie umfasst, die aus dem sinnlichen Wissen $latex K_{s}$ mittels eines Abstraktionsprozesses $latex \alpha$ erzeugt wird.

Eine Fortsetzung findet sich HIER

QUELLEN

  • Avicenny, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
  • Digital Averroes Research Environment
  • Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7

Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER.

Der Ursprung und die Evolution des Lebens auf der Erde. Leben als ein kosmischer Imperativ. Reflexionen zum Buch von Christian de Duve. Teil 3

Antikodon, Auftreten, Bedeutung, Bedeutung eines Wortes, Bedeutungskorrelat, Bedeutungsmaterial, Chaitin, DNA-Molekül, Geist, Information, Kodon, Quasikristalle, Replikation, Repräsentation, RNA - Boten (mRNA), RNA - Ribosomal, RNA - Transfer (tRNA), RNA-Molekül, Semetische Evolution, Semiotik, Shannon, Translation, Uncategorized, Virus, Zeichen, Zeichenbegriff, Zeichenmaterial

Christian de Duve, VITAL DUST. Life as a Cosmic Imperative, New York: Basic Books, 1995

Beginn: 25.Okt.2012, 23:30h
Letzte Änderung: 10.Nov. 2012, 10:30h

Für Teil2 siehe HIER

  1. [ANMERKUNG: Obwohl Duve den Begriff der Information im Text immer wieder verwendet, wird der Begriff bislang nicht definiert. Selbst an der Stelle, an der er vom Ende der chemischen Evolution spricht, die dann mit Hilfe von DNA/ RNA in die informationsgeleitete Entwicklung übergeht, findet man keine weitere Erklärung. Der einzige greifbare Anhaltspunkt ist der Bezug zur DNA/ RNA, wobei offen bleibt, warum die DNA der RNA vorgeschaltet wurde.]
  2. Duve beschreibt den Kernsachverhalt so, dass wir ein Abhängigkeitsverhältnis haben von der DNA (die zur Replikation fähig ist) über eine Transkription zur RNA (die in speziellen Fällen, Viren, auch zur Replikation fähig ist) mittels Translation (Übersetzung) zu den Proteinen (vgl. S.55f) ; von den Proteinen gäbe es keinen Weg zurück zur RNA (vgl. S.56f). Die RNA hat dabei auch eine enzymatisch-katalytische Rolle.
  3. [ANMERKUNG: Für einen Interpretationsversuch zur möglichen Bedeutung des Begriffs ‚Information‘ in diesem Kontext bietet sich vor allem der Sachverhalt an, dass die ‚Konstruktion‘ eines DNA-Moleküls bzgl. der Anordnung der einzelnen Aminosäurebausteinen nicht deterministisch festgelegt ist. Ist erst einmal ein DNA-Molekül ‚zustande gekommen‘, dann kann es innerhalb des Replikationsmechanismus (kopieren, mischen und mutieren) so verändert werden, dass es nach der Replikation ‚anders‘ aussieht. Diese nicht-deterministischen Veränderungsprozesse sind völlig unabhängig von ihrer möglichen ‚Bedeutung‘! Es ist etwa so, wie ein kleines Kind, das mit einem Haufen von Buchstaben spielen würde, allerdings mit der kleinen Vorgabe, dass es eine fertige ‚Kette‘ von Buchstaben bekommen würde, die es zerschneiden darf, neu zusammenfügen, und gelegentlich einzelne Stellen austauschen darf.
  4. Die Übersetzung dieser DNA-Ketten in Proteine erfolgt dann über den RNA-gesteuerten Mechanismus. Diese Übersetzung folgt ‚in sich‘ festen Regeln, ist von daher im Prinzip deterministisch. Dies bedeutet, dass ohne die DNA-Ketten zwar deterministische Prozesse möglich sind, allerdings ohne die ‚freie Kombinierbarkeit‘ wie im Falle der DNA-Ketten (was aber, siehe Viren, im Prinzp auch gehen könnte). Die standardmäßige Trennung von Replikation und Translation deutet indirekt daraufhin, dass mit dieser Trennung irgendwelche ‚Vorteile‘ einher zugehen scheinen.
  5. Der Clou scheint also darin zu liegen, dass durch die Entkopplung von chemisch fixierten (deterministischen) Übersetzungsmechanismen von den freien erinnerungs- und zufallsgesteuerten Generierungen von DNA-Ketten überhaupt erst die Voraussetzung geschaffen wurde, dass sich das ‚Zeichenmaterial‘ von dem ‚Bedeutungsmaterial‘ trennen konnte. Damit wiederum wurde überhaupt erst die Voraussetzung für die Entstehung von ‚Zeichen‘ im semiotischen Sinne geschaffen (zu ‚Zeichen‘ und ’semiotisch‘ siehe Noeth (2000)). Denn nur dann, wenn die Zuordnung zwischen dem ‚Zeichenmaterial‘ und dem möglichen ‚Bedeutungsmaterial‘ nicht fixiert ist, kann man von einem Zeichen im semiotischen Sinne sprechen. Wir haben es also hier mit der Geburt des Zeichens zu tun (und damit, wenn man dies unbedingt will, von den ersten unübersehbaren Anzeichen von Geist!!!).
  6. Die Rede von der Information ist in diesem Kontext daher mindestens missverständlich, wenn nicht gar schlichtweg falsch. Bislang gibt es überhaupt keine allgemeine Definition von Information. Der Shannonsche Informationsbegriff (siehe Shannon und Weaver (1948)) bezieht sich ausschließlich auf Verteilungseigenschaften von Elementen einer endlichen Menge von Elementen, die als Zeichenmaterial (Alphabet) in einem technischen Übermittlungsprozeß benutzt werden, völlig unabhängig von ihrer möglichen Bedeutung. Mit Zeichen im semiotischen Sinne haben diese Alphabetelemente nichts zu tun. Daher kann Shannon in seiner Theorie sagen, dass ein Element umso ‚wichtiger‘ ist, je seltener es ist.  Hier von ‚Information‘ zu sprechen ist technisch möglich, wenn man weiß, was man definiert; diese Art von Information hat aber mit der ‚Bedeutung‘ von Zeichen bzw. der ‚Bedeutung‘ im Kontext von DNA-Ketten nichts zu tun. Die Shannonsche Information gab und gibt es auch unabhängig von der Konstellation DNA – RNA – Proteine.
  7. Auch der Informationsbegriff von Chaitin (1987, 2001) bezieht sich ausschließlich auf Verteilungseigenschaften von Zeichenketten. Je weniger ‚Zufall‘ bei der Bildung solcher Ketten eine Rolle spielt, also je mehr ‚regelhafte Wiederholungen (Muster, Pattern)‘ auftreten, um so eher kann man diese Ketten komprimieren. Benutzt man dann dazu das Shannonsche Konzept, dass der ‚Informationsgehalt‘ (wohlgemerkt ‚Gehalt‘ hier nicht im Sinne von ‚Bedeutung‘ sondern im Sinne von ‚Seltenheit‘!) umso größer sei, je ’seltener‘ ein Element auftritt, dann nimmt der Informationsgehalt von Zeichenketten mit der Zunahme von Wiederholungen ab. Insofern Zeichenketten bei Chaitin Algorithmen repräsentieren können, also mögliche Anweisungen für eine rechnende Maschine, dann hätten nach dieser Terminologie jene Algorithmen den höchsten ‚Informationsgehalt (im Sinne von Shannon)‘, die die wenigsten ‚Wiederholungen‘ aufwiesen; das wären genau jene, die durch eine ‚zufällige Bildung‘ zustande kommen.
  8. Lassen wir den weiteren Aspekt mit der Verarbeitung durch eine rechnende Maschine hier momentan mal außer Betracht (sollte wir später aber noch weiter diskutieren), dann hätten DNA-Ketten aufgrund ihrer zufälligen Bildung von ihrer Entstehung her einen maximale Informationsgehalt (was die Verteilung betrifft).
  9. Die Aussage, dass mit der DNA-RNA die ‚Information‘ in das Geschehen eingreift, ist also eher nichtssagend bzw. falsch. Dennoch machen die speziellen Informationsbegriffe von Shannon und Chaitin etwas deutlich, was die Ungeheuerlichkeit an der ‚Geburt des Zeichens‘ verstärkt: die zufallsgesteuerte Konstruktion von DNA-Ketten verleiht ihnen nicht nur eine minimale Redundanz (Shannon, Chaitin) sondern lässt die Frage aufkommen, wie es möglich ist, dass ‚zufällige‘ DNA-Ketten über ihre RNA-Interpretation, die in sich ‚fixiert‘ ist, Protein-Strukturen beschreiben können, die in der vorausgesetzten Welt lebensfähig sind? Zwar gibt es im Kontext der biologischen (= zeichengesteuerten) Evolution noch das Moment der ‚Selektion‘ durch die Umwelt, aber interessant ist ja, wie es durch einen rein ‚zufallsgesteuerten‘ DNA-Bildungsprozess zu Ketten kommen kann, die sich dann ‚positiv‘ selektieren lassen. Dieses Paradox wird umso stärker, je komplexer die Proteinstrukturen sind, die auf diese Weise erzeugt werden. Die ‚Geordnetheit‘ schon einer einzigen Zelle ist so immens groß, dass eine Beschreibung dieser Geordnetheit durch einen ‚zufälligen‘ Prozess absurd erscheint. Offensichtlich gibt es hier noch einen weiteren Faktor, der bislang nicht klar identifiziert wurde (und der muss im Generierungsprozess von DNA-Ketten stecken).]
  10. [ANMERKUNG: Eine erste Antwort steckt vielleicht in den spekulativen Überlegungen von Duve, wenn er die Arbeiten von Spiegelmann (1967), Orgel (1979) und Eigen (1981) diskutiert (vgl. S.57-62). Diese Arbeiten deuten daraufhin, dass RNA-Molküle Replizieren können und Ansätze zu evolutionären Prozessen aufweisen. Andererseits sind RNA-Moleküle durch Übersetzungsprozesse an Proteinstrukturen gekoppelt. Wenn also beispielsweise die RNA-Moleküle vor den DNA-Ketten auftraten, dann gab es schon RNA-Ketten, die sich in ihrer jeweiligen Umgebung ‚bewährt‘ hatten. Wenn nun — auf eine Weise, die Duve nicht beschreibt — zusätzlich zu den RNA-Ketten DNA-Ketten entstanden sind, die primär nur zur Replikation da waren und die RNA-Ketten dann ’nur‘ noch für die Übersetzung in Proteinstrukturen ‚zuständig‘ waren, dann haben die DNA-Ketten nicht bei ‚Null‘ begonnen sondern repräsentierten potentielle Proteinstrukturen, die sich schon ‚bewährt‘ hatten. Der Replikationsmechanismus stellte damit eine lokale Strategie dar, wie die im realen Raum vorhandenen DNA/ RNA-Ketten den ‚unbekannten Raum‘ möglicher weiterer Proteinstrukturen dadurch ‚absuchen‘ konnten, dass neue ‚Suchanfragen‘ in Form neuer DNA-Moleküle gebildet wurden. Der ‚Akteur‘ war in diesem Fall die komplette Umgebung (Teil der Erde), die mit ihren physikalisch-chemischen Eigenschaften diese Replikationsprozesse ‚induzierte‘. Die einzige Voraussetzung für einen möglichen Erfolg dieser Strategie bestand darin, dass die ‚Sprache der DNA‘ ‚ausdrucksstark‘ genug war, alle für das ‚hochorganisierte Leben‘ notwendigen ‚Ausdrücke‘ ‚bilden‘ zu können. Betrachtet man den RNA-Proteinkonstruktionsprozess als die ‚Maschine‘ und die DNA-Ketten als die ‚Anweisungen‘, dann muss es zwischen der RNA-Proteinmaschine‘ und den DNA-Anweisungen eine hinreichende Entsprechung geben.]
  11. [ANMERKUNG: Die Überlegungen von Duve haben einen weiteren kritischen Punkt erreicht. Um die Optimierung des Zusammenspiels zwischen RNA und Proteinen und ihren Vorformen erklären zu können, benötigt er einen Rückkopplungsmechanismus, der ein schon vorhandenes ‚Zusammenspiel‘ von allen beteiligten Komponenten in einer gemeinsamen übergeordneten Einheit voraussetzt. Diese hypothetische übergeordnete gemeinsame Einheit nennt er ‚Protozelle‘ (‚protocell‘). (vgl.S.65f)]
  12. Die Protein-Erzeugungsmaschinerie (‚proteine-synthesizing machinery‘) besteht aus mehreren Komponenten. (i) Das Ribosom heftet eine Aminosäure an eine wachsende Peptid-Kette, quasi ‚blindlings‘ entsprechend den determinierenden chemischen Eigenschaften. (vgl. S.66) Das Bindeglied zwischen den ‚informierenden‘ Aminosäuren und den zu bildenden Petidketten (Proteinen) bildet die ‚Boten-RNA‘ (‚messenger RNA, mRNA‘), in der jeweils 3 Aminosäuren (Aminosäuren-Triplets) als ‚Kodon‘, also 4^3=64, eine von 64 möglichen Zieleinheiten kodieren. Dem Kodon entspricht in einer ‚Transport-RNA‘ (‚transfer-RNA, tRNA‘) dann ein ‚Antikodon‘ (ein chemisch komplementäres Aminosäure-Triplet), an das genau eine von den 22 (21) biogenen Aminosäuren ‚angehängt‘ ist. Durch diesen deterministischen Zuordnungsprozess von mRNA-Kodon zu tRNA-Antikodon und dann Aminosäure kann eine Peptidkette (Protein) Schritt für Schritt entstehen. Diejenigen Zieleinheiten aus den 64 Möglichen, die nicht in eine Aminosäure übersetzt werden, bilden ‚Befehle‘ für die ‚Arbeitsweise‘ wie z.B. ‚Start‘, ‚Stopp‘. Dieser ‚Kode‘ soll nach Duve ‚universal‘ für alle Lebewesen gelten. (vgl. S.66f)
  13. [ANMERKUNG: Für eine vergleichende Lektüre zu diesem zentralen Vorgang der Proteinbildung sei empfohlen, die immer sehr aktuellen Versionen der entsprechenden englischsprachigen Wikipediabeiträge zu lesen (siehe unten Wkipedia (en).]
  14. Duve weist ausdrücklich darauf hin, dass die eigentliche ‚Übersetzung‘, die eigentliche ‚Kodierung‘ außerhalb, vorab zu dem mRNA-tRNA Mechanismus liegt. Der ribosomale Konstruktionsprozess übernimmt ja einfach die Zuordnung von Antikodon und Aminosäure, wie sie die Transfer-RNA liefert. Wann, wie und wo kam es aber zur Kodierung von Antikodon und Aminosäure in dem Format, das dann schließlich zum ‚Standard‘ wurde? (vgl. S.69)
  15. Letztlich scheint Duve an diesem Punkt auf der Stelle zu treten. Er wiederholt hier nur die Tatsachen, dass RNA-Moleküle mindestens in der dreifachen Funktionalität (Botschaft, Transfer und Konformal) auftreten können und dass sich diese drei Funktionen beim Zusammenbauen von Peptidketten ergänzen. Er projiziert diese Möglichkeit in die Vergangenheit als möglichen Erklärungsansatz, wobei diese reine Möglichkeit der Peptidwerdung keinen direkten ‚evolutionären Fitnesswert‘ erkennen lässt, der einen bestimmte Entwicklungsprozess steuern könnte.(vgl. S.69f) Er präzisiert weiter, dass der ‚Optimierung‘ darin bestanden haben muss, dass — in einer ersten Phase — ein bestimmtes Transfer-RNA Molekül hochspezifisch nur eine bestimmte Aminosäure kodiert. In einer nachfolgenden Phase konzentrierte sich die Optimierung dann auf die Auswahl der richtigen Boten-RNA. (vgl.S.70f)
  16. [ANMERKUNG: Das alles ist hochspekulativ. Andererseits, die ‚Dunkelheit‘ des Entstehungsprozesses ist nicht ‚völlige Schwärze‘, sondern eher ein ’nebliges Grau‘, da man sich zumindest grundsätzlich Mechanismen vorstellen kann, wie es gewesen sein könnte.]
  17. Duve reflektiert auch über mögliche chemische Präferenzen und Beschränkungen innerhalb der Bildung der Zuordnung (= Kodierung) von Kodons und Antikodons mit der Einschätzung, dass die fassbaren chemischen Eigenschaften darauf hindeuten, dass eine solche Zuordnung nicht ohne jede Beschränkung, sprich ’nicht rein zufällig‘ stattgefunden hat.(vgl. S.72f)
  18. [ANMERKUNG: Der spekulative Charakter bleibt, nicht zuletzt auch deswegen, weil Duve schon für den ‚evolutionären‘ Charakter der Kodon-Antikodon Entwicklung das fiktive Konzept einer ‚Protozelle‘ voraussetzen muss, deren Verfügbarkeit vollständig im Dunkel liegt. Etwas kaum Verstandenes (= die Kodon-Antikodon Zuordnung) wird durch etwas an dieser Stelle vollständig Unverstandenes (= das Konzept der Protozelle) ‚erklärt‘. Natürlich ist dies keine echte Kritik an Duve; schließlich versucht er ja — und darin mutig — im Nebel der verfügbaren Hypothesen einen Weg zu finden, der vielleicht weiter führen könnte. In solchen unbefriedigenden Situationen wäre eine ‚vornehme Zurückhaltung‘ fehl am Platze; Suchen ist allemal gefährlich… ]
  19. Duve geht jedenfalls von der Annahme aus, dass ein evolutionärer Prozess nur in dem Umfang effektiv einsetzen konnte, als die Veränderung der Kodon-Antikodon Zuordnung samt den daraus resultierenden chemischen Prozessen (Katalysen, Metabolismus…) insgesamt ein Trägersystem — in diesem Fall die vorausgesetzte Protozelle — ‚positiv‘ unterstützte und ‚überlebensfähiger‘ machte. (vgl. S.73f)
  20. Ungeachtet der Schwierigkeit, die Details des Entstehungsprozesses zum jetzigen Zeitpunkt zu enthüllen, versucht Duve weitere Argumente zu versammeln, die aufgrund allgemeiner Eigenschaften des Entstehungsprozesses den evolutionären Charakter dieses Prozesses weiter untermauern.
  21. Generell gehört es zu einem evolutionären Prozess, dass die Entwicklung zum Zeitpunkt t nur auf das zurückgreifen kann, was an Möglichkeiten zum Zeitpunkt t-1 zur Verfügung gestellt wird, also change: STATE —> STATE. Dies schränkt den Raum der Möglichkeiten grundsätzlich stark ein. (vgl. S.75, 77)
  22. Da es bei der Übersetzung von mRNA in Peptide zu Fehlern kommen kann (Duve zitiert Eigen mit der quantitativen Angabe, dass auf 70 – 100 übersetzten Aminosäuren 1 Baustein falsch ist ), bedeutet dies dass die ersten Kodon-Antikodon Zuordnungen in Gestalt von mRNA Molekülen aufgrund dieser Fehlerrate nur 60 – 90 Einheiten lang sein konnten, also nur 20 – 30 Aminosäuren kodieren konnten. (vgl. S.76)
  23. Rein kombinatorisch umfasst der Möglichkeitsraum bei 20 Aminosäuren 20^n viele Varianten, also schon bei einer Länge von nur 100 Aminosäuren 10^130 verschiedene Moleküle. Rein praktisch erscheint nach Duve ein solcher Möglichkeitsraum zu groß. Nimmt man hingegen an — was nach Duve der tatsächlichen historischen Situation eher entsprechen soll –, dass es zu Beginn nur 8 verschiedene Aminosäuren gab die zu Ketten mit n=20 verknüpft wurden, dann hätte man nur 8^20 = 10^18 Möglichkeiten zu untersuchen. In einem kleinen Tümpel (‚pond‘) erscheint das ‚Ausprobieren‘ von 10^18 Variationen nach Duve nicht unrealistisch.(vgl. S.76)
  24. Schließlich führt Duve noch das Prinzip der ‚Modularität‘ ein: RNA-Moleküle werde nicht einfach nur ‚Elementweise‘ verlängert, sondern ganze ‚Blöcke‘ von erprobten Sequenzen werden kombiniert. Dies reduziert einserseits den kombinatorischen Raum drastisch, andererseits erhöht dies die Stabilität. (vgl. S.77)

Fortsetzung folgt…

LITERATURVERWEISE

Chaitin, G.J; Algorithmic information theory. Cambridge: UK, Cambridge University Press, (first:1987), rev.ed. 1988, 1990, 1992, ,paperback 2004

Chaitin, G.J; Exploring Randomness. London: UK, Springer Ltd., (2001, corr. 2001), 3rd printing 2002

Noeth, W., Handbuch der Semiotik, 2. vollst. neu bearb. und erw. Aufl. mit 89 Abb. Stuttgart/Weimar: J.B. Metzler, xii + 668pp, 2000

Claude E. Shannon A mathematical theory of communication. Bell System Tech. J., 27:379-423, 623-656, July, Oct. 1948 (online: http://cm.bell-labs.com/cm/ms/what/shannonday/paper.html; zuletzt besucht: May-15, 2008)

Claude E. Shannon; Warren Weaver The mathematical theory of communication. Urbana – Chicgo: University of Illinois Press, 1948.

Wikipedia (en): Genetischer Kode: http://en.wikipedia.org/wiki/Genetic_code, Ribosom: http://en.wikipedia.org/wiki/Ribosome, Protein Biosynthesis: http://en.wikipedia.org/wiki/Protein_biosynthesis, Aminosäuren: http://en.wikipedia.org/wiki/Amino_acid, Proteinoide Aminosäuren:http://en.wikipedia.org/wiki/Proteinogenic_amino_acid (Alle Links zuletzt besucht: Mo, 29.Okt.2012)

Für einen Überblick über alle bisherigen Einträge nach Titeln siehe HIER.

WANN IST EIN MENSCH AUTHENTISCH?

Allgemein, authentisch, Bedeutung, Bedeutung - abstraktes Konstrukt, Bedeutung - empirisch, Bedeutung eines Wortes, in dubio pro reo, Worterkennung

 

  1. Das gesprochene Wort ‚authentisch‘: ein einzelner Mensch kann das Wort ‚authentisch‘ im Deutschen ganz unterschiedlich aussprechen (langsam, schnell, laut, leise, mit speziellen Betonungen…). Beim Sprechen wird ein veränderlicher Schalldruck erzeugt, den man messen kann (z.B. mit einem Mikrophon, analog) und dann ‚digitalisieren‘. Diese besteht in einer periodischen (1x pro Sekunde, 10x, 1000x, …) Abtastung des analogen Signals mit einer bestimmten ‚Bitauflösung‘ (2 Bit, 4, 8, 16 ….). Damit entsteht eine Zahlenfolge, die jeweils verschieden ist. Ein Computerprogramm ohne ‚Vorwissen‘, könnte damit nicht viel anfangen. Sprecher der deutschen Sprache sind aber in der Regel in der Lage, die verschiedenen lautlichen Realisierungen des einen gesprochenen Wortes als ‚das gleiche Wort‘ zu erkennen. Dies bedeutet, dass unser Gehirn verbunden mit dem Gehörorgan in der Lage ist, bei unterschiedlichen Schallobjekten ‚Gemeinsamkeiten‘ zu erkennen, die nicht ‚unmittelbar‘ im Schall selbst präsent sind. Menschen können – bei ein bischen Training – ‚Lautbestandteile‘ an einem Wort unterscheiden (Konsonanten, Vokale, Halbsilben, Silben, Morpheme,…), die ein Computerprogramm nur mit erheblichem Aufwand zu identifizieren in der Lage ist (die heute (August 2012) käuflich erhältlichen Programme zum Diktieren können dies immer noch nur sehr begrenzt!). Zu fragen, was denn die ‚richtige‘ Aussprache des Wortes ‚authentisch‘ sei, hängt also von dieser besonderen Fähigkeit des menschlichen Gehirns ab und ist — von daher schwierig. Das, was jeder Mensch jeweils als ‚das Gemeinsame‘ in den unterschiedlichen Aussprachen (‚Realisierungen‘) des einen Wortes ‚authentisch‘ ‚erkennt‘, ist selbst nicht ‚vorzeigbar‘. Es existiert nur im individuellen Erkennen. Dass es dieses ‚Gemeinsame‘ gibt, erkennen wir indirekt daran, dass ein Mensch bei unterschiedlicher Aussprache immer das gleiche Wort auf einen Zettel ’schreiben‘ könnte (wobei das ‚Schreiben‘ eine eigenständige Leistung ist. Sogenannte ‚Analphabeten‘ können sprechen, aber nicht schreiben). Sprachgemeinschaften versuchen zwar, eine ‚offizielle Aussprache‘ zu ’normieren‘ (das ‚Hochdeutsche‘, das ‚Bühnendeutsch‘ der Nachrichtensprecher, usw.), doch können diese Normierungen letztlich nur grobe Leitlinien sein, die — aufgrund des Sachverhalts — niemals vollständig eindeutig sein können. Halten wir fest: schon das gesprochene Wort als primäres Mittel sprachlicher Kommunikation existiert in Realisierungsformen, die eine letzte Eindeutigkeit nicht zulassen; man braucht eine Vielzahl von Beispielen, man braucht Hypothesen (Annahmen, Vermutungen), man ’nähert sich an‘, man operiert mit einem ’subjektivem Konstrukt‘ auf der Basis ‚empirischer Ereignisse‘.

  2. Die Bedeutung des Wortes ‚authentisch‘: Ein Lautereignis als solches hat normalerweise keine Bedeutung. Wenn ich im Deutschen Laute äußern würde, die sich schriftlich in etwa als ‚Dididu‘, ‚Garseku‘, ‚Uklukl‘ usw. repräsentieren lassen, dann wird normalerweise niemand etwas damit anfangen können. Äußerungen, die sich schriftlich in etwa als ‚Haus‘, ‚Tasse‘, ‚Stuhl‘ usw. repräsentieren lassen (und die sich lautlich als ‚das gleiche Wort‘ identifizieren lassen), würde man sehr wohl als ‚bedeutsam‘ einstufen. Eine lautliche Äußerung, die sich als ‚Stuhl‘ aufschreiben lässt, verbindet man mit ‚etwas anderem‘, eben jenem, was man ‚meint‘, wenn man das Wort ‚Stuhl‘ äußert. Dieses ‚andere Gemeinte‘ konstituiert dann die ‚Bedeutung‘ des lautlichen Ereignisses ‚Stuhl‘. Dieses ‚Andere‘ zum gesprochenen Wort, das seine ‚Bedeutung‘ konstituieren kann, ist auch wieder – im einfachen Fall – ein ‚Wahrgenommenes‘ (sichtbar, hörbar, tastbar, schmeckbar,…), das in verschiedenen Realisierungen vorkommt: dasselbe ‚Stuhlobjekt‘ aus verschiedenen Perspektiven, mit verschiedenen Beleuchtungsverhältnissen in unterschiedlichen Kontexten, oder aber ‚unterschiedliche‘ Stuhlobjekte (Farben, Materialien, Abmessungen, Formen,…) (auch hier würde eine einfache Digitalisierung z.B. der visuellen Signale einer Videokamera Zahlenkolonnen erzeugen, die selbst bei dem gleichen Stuhlobjekt völlig verschieden wären. Ein Computerprogramm ohne ‚Vorwissen‘ würde nichts erkennen können). Aber auch in diesem Fall besitzt das menschliche Gehirn im Verbund mit den verschiedenen Sinnesorganen (Sehsinn, Höhrsinn, Tastsinn,…) die erstaunliche Fähigkeit, in der Vielzahl der Eindrücke ‚Gemeinsamkeiten‘ zu erkennen, aufgrund deren dann ein Mensch (z.B. ein Kind, das Sprache lernt) bei einem bestimmten Stuhlobjekt trotz wechselndem Standpunkt, wechselnder Perspektive, unterschiedlichem Abstand, unterschiedlicher Beleuchtung dieses Stuhlobjekt als das ‚gleiche Objekt‘ in den unterschiedlichen Wahrnehmungsrealisierungen zu erkennen. Diese Fähigkeit des Erkennens von ‚Gemeinsamkeiten‘ in ‚veränderlichen Details‘ ist eine entscheidende Fähigkeit zum Erkennen überhaupt (heute käufliche Computerprogramme zur Objekterkennung sind hier mittlerweile erstaunlich weit gekommen, zumindest wenn man auf bestimmte Teilaspekte abhebt (z.B. Gesichtserkennung)). Aber auch hier gilt, dass der entscheidende Aspekt des ‚Erkennens‘ nicht in der aktuellen Realisierung eines Objektes liegt, sondern in dem ’subjektiven Konstrukt‘ eines Gehirns, das sich anlässlich der unterschiedlichen ‚empirischen Realisierungen‘ eines Objektes ‚bildet‘. Dieses ’subjektive Konstrukt‘ Cog(Perc(EObj)) = CObj eines ‚kognitiven Objektes‘ anlässlich unterschiedlicher ‚empirisches Objekte‘ ist aber – wie schon im Falle des subjektiven Konstrukts des gesprochenen Wortes – selbst nicht ‚vorzeigbar‘, sondern existiert nur ‚intern‘, als ‚gewusstes Etwas‘, indirekt erkennbar an einem bestimmten ‚Verhalten‘, z.B. daran, dass ein Mensch bei ‚ein und demselben Objekt‘ immer das ‚gleiche Wort‘ benutzt, obwohl er das empirische Objekt unterschiedlich realisiert wahrnimmt. Dies hat zur Folge, dass die ‚gemeinte Bedeutung‘ eines Wortes wie ‚Stuhl‘ grundsätzlich niemals ‚eindeutig‘ sein kann noch jemals ‚abgeschlossen‘ ist. Neue Stuhlereignisse können das bisherige subjektive Konstrukt ‚verändern‘, und diese Veränderungen sind von Mensch zu Mensch verschieden und sie sind dem einzelnen Menschen selbst nicht notwendigerweise ‚bewusst‘! Man merkt solche Veränderungen des subjektiven Erkenntnisstandes oft erst dann, wenn man in einer Gesprächssituation feststellen darf, dass der Gesprächspartner aktuell einen anderen ‚Aspekt‘ des Objektes ‚thematisiert‘ als man selbst bereit oder fähig ist, zu thematisieren. Halten wir fest: die subjektive Bedeutung von empirischen Ereignissen ist der eigentliche Kern sprachlicher Bedeutungen, diese selbst sind dynamische Gebilde, als solche nicht vorzeigbar, teilweise dem Sprecher selbst nicht ‚bewusst‘ und bilden sich interaktiv in gemeinsame geteilten Sprechsituationen.

  3. Im Fall des Wortes ‚authentisch‘ kommt noch ein weiterer Aspekt hinzu: während ‚empirisch aufweisbare‘ Objekte wie ‚Stuhl‘, ‚Tisch‘, ‚Tasse‘ für alle beteiligten Sprecher einen ‚gemeinsamen objektiven Referenzpunkt‘ bilde können, an dem die verschiedenen Sprachteilnehmer ihre ‚Bedeutungshypothesen‘ ‚ausrichten‘, gibt es Worte – wie das Wort ‚authentisch‘ –, die nicht als ‚einfache empirische Objekte‘ vorkommen. Zu sagen, ein Mensch sei ‚authentisch‘ kann sich prinzipiell auf sämtliche Aktivitäten dieses Menschen beziehen, auf sämtliche Situationen, in denen er auftritt. Faktisch wird man sich meistens auf eine Auswahl beschränken, da normalerweise niemand das vollständige Verhalten eines Menschen untersuchen kann (wie ja auch der einzelne Mensch von sich selbst nur eine sehr begrenzte Kenntnis hat (weil man vieles vergisst, weil die Selbstwahrnehmung unvollständig ist, weil das Verständnis von einem selbst unvollständig oder unpassend ist,….). Man hat also normalerweise eine kleine Auswahl von Fragmenten eines komplexen Geschehens, dessen Randbedingungen einem nur unvollständig zugänglich sind (z.B. hat man keine direkten Kenntnisse von den inneren (subjektiven) Zuständen, die einen Menschen dazu bringen, etwas Bestimmtes zu tun). Will man in solch einer komplexen und unübersichtlichen Situation dennoch einen Bedeutungsinhalt konstruieren, der eine minimale ‚Gemeinsamkeit‘ zwischen verschiedenen Sprechern erlaubt, dann kann dies nur dadurch geschehen, dass es ‚Standardsituationen‘ und ‚Standardverhaltensweisen‘ gibt, die sich von allen Beteiligten hinreichend identifizieren lassen und die man als ‚Kriterium‘ benutzen kann, um zur ‚Einschätzung‘ zu kommen, jemand sei ‚authentisch‘ oder nicht.

  4. Fragt man sich, wie solche ‚Standardsituationen‘ und ‚Standardverhaltensweisen‘ aussehen könnten, dann benötigt man etwas ‚Allgemeines‘, das über einzelne konkrete Ereignisse hinausreicht, so, dass man sagen könnte, dass diese oder jene konkrete Verhaltensweise ‚Beispiele‘ für dieses ‚Allgemeine‘ sind (z.B.  Formulierungen wie ‚X kocht‘, ‚X hebt Geld ab‘, ‚X macht Musik‘, ‚X lernt gerade‘,… als Beispiele für etwas Allgemeines, dem sich ein konkretes individuelles Verhalten zuordnen lässt). Die Gesetzgebung — wie auch unterschiedliche Normierungen — sind ein Beispiel dafür, wie man versucht, mittels Texten Situationen so zu beschreiben, dass man im Einzelfall entscheiden kann, ob die Handlung einer Person solch einer Beschreibung subsumiert werden kann und ein Richter feststellen kann, ob eine Person mit diesem Verhalten im Sinne dieser Beschreibung ’straffällig‘ geworden ist oder nicht. Wie man aus der Praxis der Rechtsfindung weiß, ist dies alles andere als einfach und ganz selten eindeutig. Letztlich sind es die aktiven Richter, die darüber ‚befinden‘, ob bestimmte Ereignisse als unter eine Beschreibung ’subsumierbar‘ anzusehen sind oder nicht. Im alten lateinischen Spruch ‚in dubio pro reo‘ (Etwa „Im Zweifel für den Angeklagten“), drückt sich schlagwortartig diese Einsicht in die Begrenztheit der Erkenntnis aus, so dass man im Strafprozess einen Angeklagten aufgrund der notorisch schwierigen Erkenntnislage nicht verurteilen sollte, wenn Zweifel an seiner Schuld verbleiben.

  5. Was wären ‚Standardsituationen‘ für ‚authentische‘ Menschen? Wenn jemand – ohne erkennbare Not — sagt, er heiße ABC, laut Ausweis aber CAB heißt, wäre dies vielleicht ein Grenzfall (ein Scherz? Schauspielerei? Vorgauklung falscher Tatsachen?..). Wenn jemand (ebenfalls ohne Not) sagt, er übe Position XYZ in einer Institution aus oder den Beruf XYZ, tatsächlich aber nicht, wäre dies eher kein Beispiel für ‚Authentizität‘? Wenn jemand nichts vom modernen Modebetrieb hält, sich aber dennoch bestimmte Kleidungsstücke anzieht, weil dies die mediengesteuerte Mehrheit in einer bestimmten soziologischen Gruppe ’so tut‘, ist dies ‚Anpassung‘, ‚Unterwerfung‘ – und damit nicht authentisch – oder ist dies ‚Pragmatismus‘, ‚Klugheit‘ und dadurch noch authentisch? Wenn jemand in Gesprächen mit KollegenInnen eine ‚Rolle‘ spielt, von der er/sie meint, damit komme er/sie ‚gut an‘, obgleich er/sie tatsächlich andere Meinungen und Werte haben, wäre dies auch ein Grenzfall; eher kein Fall von Authentizität? Was aber, wenn bestimmte berufliche Positionen nur erreicht werden können, wenn man einer Mehrheit ‚gefällt‘, deren Meinung man nur bedingt teilt. Gibt man sich auf, ‚verrät‘ man sich, wenn man dann ’so tut‘, ‚als ob‘ man diese Meinungen vertritt, um die Position zu bekommen? Falls die Position selbst dann Handlungen ermöglicht, hinter denen man stehen kann, wäre der Weg zu dieser Position dann ein ‚Kompromiss‘ (?), um etwas ‚Gutes‘ zu erreichen. Wäre dies ‚authentisch‘? Wenn aber die Position selbst weitgehend Handlungen erfordert, hinter denen man nicht wirklich steht, würde dies jede ‚Authentizität‘ ausschließen?

  6. Schon diese wenigen Beispiele zeigen, dass offensichtlich Handlungen als solche nicht direkt etwas über ‚Authentizität‘ aussagen, da die Umstände von Handlungen sehr vielschichtig sein können und die ‚Bedeutung‘ einzelner Momente sich nur im Gesamtkontext erschließt.

  7. Was kann es aber unabhängig von bestimmten Handlungsabläufen geben, was sich in all den verschiedenen Situationen ‚durchhält‘? Ferner muss man auch fragen, ob es unbedingt ‚für andere erkennbar‘ sein muss? Kann es nicht sogar sein, dass ein Mensch ’sich selbst treu‘ bleibt, wenn er in verschiedenen Situationen und Lebensphasen ganz unterschiedliche Dinge tut, in denen ein ‚Außenstehender‘ nur ‚Widersprüchliches‘ erkennt obwohl es aus Sicht des Handelnden einen ‚roten Faden‘ gibt. Wäre solch ein Mensch ‚authentisch‘ … sozusagen mit einer verborgenen Authentizität? Wäre ‚das Authentische‘ dann eher eine subjektive Kategorie, ein ’sich selbst treu bleiben‘ im Laufe unterschiedlichster Situationen? Wenn wir aber annehmen müssen, dass das Bild von einem selbst sehr fehleranfällig, sehr unvollständig ist, dann wäre eine Authentizität, die sich an diesem problematischen Selbstbild orientiert, nicht minder problematisch und fehleranfällig.

  8. Möglicherweise haben wir hier einen ersten ‚Ankerpunkt‘ für die Bedeutung von ‚Authentizität‘. Da wir wissen, dass jede Form von Wissen grundsätzlich unvollständig und fehleranfällig ist, bleibt uns nur die bescheidene Möglichkeit, mit dem Wenigen, was wir haben, ’sorgsam umzugehen‘. Wir können versuchen, das Wenige, was wir tatsächlich meinen zu wissen und vom dem wir glauben, dass es ‚wichtig‘ sein könnte, dieses in jeder Hinsicht so ‚transparent‘ wie möglich zu ‚bewahren‘ und es zu ‚benutzen‘. Da wir nichts anderes haben als dieses ‚Wenige‘ entscheidet Sorgsamkeit, Ehrlichkeit, Transparenz darüber, ob wir mit diesem Wenigen ‚ein Stück mehr‘ erkennen können, ‚wie es ist‘ oder nicht. In diesem Sinne ist unser eigener Umgang mit dem Wenigen, was wir haben die Voraussetzung für nächste Schritte bzw. für die Integration von einzelnen Aspekten zu größeren Zusammenhängen. Ich könnte mir vorstellen, dass wir einen Menschen, der in diesem grundlegenden Sinne ’sorgsam‘, ‚ehrlich‘, ‚transparent‘ mit sich selbst und anderen umgeht, etwas ‚Authentisches‘ hat, dass er eine ‚Atmosphäre‘ ‚ausstrahlt‘, in der man ‚vertrauen‘ kann, sich ‚entspannen‘ kann usw. Ein authentischer Mensch in diesem Sinne repräsentiert daher einen ‚Raum von Transparenz, Ehrlichkeit, Sorgsamkeit, Verantwortlichkeit‘, von der aus sich im Prinzip alles erreichen lässt, was wichtig ist, allerdings in – meistens – vielen Schritten, längeren Zeiträumen, mit viel Energie, mit viel Arbeit, mit einer ’sich selbst speisenden‘ Motivation und Zufriedenheit, die sich nicht aus ‚Sachen‘ speist, sondern aus einer Haltung, einem Prozess, einem sich daraus ergebenden Zustand.

  9. Ich glaube nicht, dass man in irgendeinem Buch (Wörterbuch, Lexikon,…) dieser Welt im einzelnen nachlesen kann, was ‚authentisch‘ ist. Wer für sich selbst diesen ‚Zustand‘ nicht selber findet, wird niemals verstehen können, was es ist (wie mit allen wichtigen Dingen). Zugleich gibt es keinen harten Grund, warum nicht grundsätzlich jeder Mensch ein ‚authentischer Mensch‘ werden könnte, wenngleich Schmerzen, Folter, Terror, Überlebenskampf und dergleichen starke Faktoren sind, die einen Menschen darin behindern können. Doch gibt es viele Beispiele, wo Menschen selbst unter solchen extremen Umständen ihren authentischen Charakter beibehalten haben. Letztlich gibt es für uns Menschen auch keine wirkliche Alternative zum Authentischsein. Wer in den elementaren Dingen des Lebens Kompromisse mit dem Nicht-Authentischen eingeht, zerstört letztlich seine eigene Lebensgrundlage und damit meistens auch die Lebensgrundlage von anderen Menschen. Wir sind niemals alleine: weder im Empfangen noch im Geben. Die Vorstellung des Alleine-Seins ist ein tragischer Irrtum, der den Keim der Lüge und Unwahrheit von Anbeginn in sich trägt und mehr zur Selbstzerstörung beiträgt als alles andere. Jeder Mensch braucht den anderen Menschen, und zwar so authentisch wie möglich. Leider garantiert dies keinen Erfolgt im Überlebenskampf. Ohne diese Kunst des wechselseitigen Authentischseins kann es aber auch keinen nachhaltigen Erfolg geben, da Authentischsein die Voraussetzung für wahre Erkenntnis ist, diese wiederum ist die Voraussetzung für Theorien (und Technologien), die nachhaltig funktionieren. Große Teile unserer heutigen Lebensweisen und Technologien sind dabei, die Lebensgrundlagen fast aller Arten und damit auch die des Menschen nachhaltig zu zerstören. In diesem Sinne sind sie nicht ‚wahr‘, weil wir, die Urheber und Schöpfer, nicht ausreichend authentisch sind. Wir Verschließen unsere Augen, weil wir uns wechselseitig suggerieren, so schlimm sei es doch nicht, wenn wir es im Detail nicht so genau nehmen, wenn wir uns wechselseitig verletzen und ruinieren. Doch, mit der Wahrheit lässt sich nicht spielen. Sie war schon lange vor unseren modernen Unwahrheiten dar und sie ist unvergleichlich mächtiger. Unwahrheit führt unweigerlich zum Scheitern (dazu braucht man keine ‚Pseudogötter‘ zu beschwören. Die Wahrheit selbst reicht dazu völlig aus).

Spiegelung Umwelt im Gebaeude

Eine Übersicht über alle bisherigen Themen findet sich HIER