VORGESCHICHTE
1. In einem ersten Beitrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 1 hatte ich geschildert, wie ich zur Lektüre des Textes von Avicenna gekommen bin und wie der Text grob einzuordnen ist.
2. In einem zweiten Beitrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 2 ging es um die Frage, warum überhaupt Logik? Avicenna führt erste Unterscheidungen zu verschiedenen Wissensformen ein, lässt aber alle Detailfragen noch weitgehend im Dunkeln.
3. Im Teil AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 3 ging es um einfache und zusammengesetzte Begriffe, und bei den einfachen Begriffen um ‚individuelle‘ und ‚universelle‘. Schon hier zeigt sich der fundamentale Unterschied zwischen der antiken und der modernen-formalen Logik. In der antiken Logik wird die Ausdrucksebene E – und einer sich daran manifestierenden Folgerungslogik – immer in Verbindung mit einer zugehörigen Bedeutungsstruktur gesehen, die sich an einer Objektstruktur O festmacht. Die moderne formale Logik kennt zwar auch ‚Semantiken‘ und ‚Ontologien‘, diese sind aber ’sekundär‘, d.h. es werden nur solche ‚formalen Semantiken‘ betrachtet, die zum vorausgesetzten syntaktischen Folgerungsbegriff ‚passen‘. Dies sollte dann später an konkreten Beispielen diskutiert werden. Hier liegt der Fokus auf der antiken Logik im Sinne Avicennas.
4. Im nächsten Abschnitt VICENNAS ABHANDLUNG ZUR LOGIK – Teil 4 knüpft Avicenna an den zuvor eingeführten Begriff des ‚universellen‘ Begriffs an und betrachtet jetzt solche als ‚universell‘ bezeichneten Ausdrücke in einem Ausdruckskontext von aufeinanderfolgenden Ausdrücken . Alle diese Ausdrücke könnte man im Sinne der antiken Logik auch als ‚Urteile‘ bezeichnen, durch die einem bestimmten Ausdruck durch andere Ausdrücke bestimmte Bedeutungen (Eigenschaften) zu- oder abgesprochen werden. Hier unterscheidet er die Fälle eines ‚wesentlichen‘ Zusammenhanges zwischen zwei Begriffen und eines ’nicht wesentlichen‘ – sprich ‚akzidentellen‘ – Zusammenhangs.
BEGRIFFSINFLATION
5. Im nächsten Abschnitt führt er mindestens fünf neue technische Begriffe ein, deren Erklärung partiell unvollständig bleibt. Dies ist sehr schade. Aber, versuchen wir zu verstehen, was noch verstehbar ist.
6. Es sind die Begriffe ‚Genus‘ (Gattung?), ‚Spezies‘ (Art?), Differenz, allgemeine und spezielle Akzidens, und den Begriff ‚Kategorie(n)‘.
7. Er beginnt die Diskussion mit der ‚universellen Bedeutung‘, von der er behauptet, man könne hier 5 Typen unterscheiden (ohne sie direkt anzugeben). Drei Typen von universellen Bedeutungen seien ‚wesentlich‘ und zwei ’nicht-wesentlich‘, also ‚akzidentell‘.
8. Seine Erklärungen zu den ‚wesentlich universellen‘ Bedeutungen wiederholt in gewisser Weise das bislang Gesagte, indem er das Klassifizierungsmerkmal als Frage formuliert: ‚Zu welcher Art Y von Dingen gehört eine Entität X‘? Die Antwort wäre allgemein: ‚X ist ein Y‘, eventuell noch ergänzt um charakteristische Eigenschaften wie ‚Y ist/ hat/kann … Z‘. Letztlich ist dies, wie Avicenna feststellt, eine Definition, bei der etwas Neues (das X) durch Bezugnahme auf etwas schon Bekanntes (Y) erklärt wird. Y ist eine notwendige Voraussetzung für X.
9. Als Beispiel führt er u.a. an, Frage: ‚Was ist ein X=Mensch?‘, Antwort: ‚X=Mensch ist ein Y=Lebewesen‘ (‚animal‘).
10. Allerdings benutzt er auch Beispiele, die von dem ‚üblichen‘ Konzept eines Dings (einer ‚Entität‘ (engl.: ‚entity‘)) abweichen. Statt von ‚Mensch‘, ‚Kuh‘ und ‚Pferd‘ spricht er auch von ‚Schwarzheit‘, ‚Rotheit‘ und ‚Weisheit‘ bzw. auch von ‚Drei‘, ‚Fünf‘ und ‚Zehn‘.
11. Bedeutungen X = {‚Schwarzheit‘, ‚Rotheit‘, ‚Weisheit‘} beantwortet er mit Y=Qualitäten. Bedeutungen X = {‚Drei‘, ‚Fünf‘, ‚Zehn‘} beantwortet er mit Y=Zahlen.
12. Etwas später benutzt der die Bedeutungen ‚Substanz‘, ‚Qualität‘ und ‚Quantität‘ als universelle Begriffe für die ersten Beispiele, so dass man lesen kann/ muss Wenn X= {‚Mensch‘, ‚Kuh‘ und ‚Pferd‘}, dann Y= ‚Substanz‘, wenn X = {‚Schwarzheit‘, ‚Rotheit‘, ‚Weisheit‘} dann Y=Qualität, wenn X = {‚Drei‘, ‚Fünf‘, ‚Zehn‘} dann Y=Quantität.
13. Von den ‚wesentlichen universellen‘ Begriffen ‚Substanz‘, ‚Qualität‘ und ‚Quantität‘ sagt Avicenna, dass sie sich nicht weiter verallgemeinern lassen, d.h. wenn X=Substanz, dann gibt es kein allgemeineres Y, auf das sich dieser universelle Begriff zurückführen lässt (und entsprechend für X=Qualität‘ und X=Quantität). Deshalb nennt Avicenna diese universellen Begriffe, die wesentlich keinen anderen universellen Begriff mehr ‚über sich‘ haben, ‚Kategorien‘, ohne dass er diesen Zusammenhang explizit benennt; er tut es einfach.
14. Als Beispiele für ‚akzidentelle universelle‘ Begriffe führt er an, dass ‚fest‘ (engl.: ’solid‘) allgemeiner sei als ‚Lebewesen‘, aber spezieller als ‚Substanz‘; entsprechend sei ‚Zahl‘ allgemeiner als ‚gleich‘ (engl.: ‚even‘), aber spezieller als ‚Quantität‘. ‚Gleichheit (engl.: ‚eveness‘) sei allgemeiner als ‚vier‘, doch spezieller als ‚Quantität‘.
15. Dann führt er die Begriffe ‚Genus‘ und ‚Spezies‘ ein mit der Formulierung, dass dasjenige, das allgemeiner ist, die speziellere Spezies sei, und umgekehrt, dass dasjenige, was das speziellere Universelle ist, ist die allgemeinere Spezies. Diese Formulierungen sind nicht eindeutig.
16. Später sagt er noch, dass es Dinge gibt, die sowohl Genus und Spezies sein können oder Dinge, die nur Genus sind, und nicht unter irgendeiner Spezies sind.
17. Dann folgt die Feststellung, dass die Begriffe ‚Substanz‘, ‚Qualität‘ und ‚Quantität‘ kein Genus einer Spezies seien; unter ihnen befinden sich nur Instanzen wie ‚Mensch‘, ‚Schwarzheit‘ und ‚vier‘.
18. Aus diesen Beispielen folge die Natur einer Spezies, die kein Genus sein kann, sondern nur Spezies von allen Spezies, die ‚unter‘ ihr kommen.
19. Instanzen eines wesentlichen universellen Begriffs können sich durch akzidentelle Eigenschaften unterscheiden (z.B. angenommen {X1, X2} sind beide Y und X1 ist ’schwarz‘ und X2 ‚weiß‘ und ’schwarz‘. Dann ist die Eigenschaft ’schwarz‘ allgemeiner als X1 und X2, ’schwarz‘ kommt X1 und X2 nicht wesentlich, sondern akzidentell zu, kann aber differenzierend wirken.
20. Abschließend führt Avicenna noch folgende Beispiele an: Jeder universelle Begriff ist entweder Genus, so wie ‚Lebewesen‘, oder Spezies, so wie ‚Mensch‘, oder Differenz, so wie ‚die Fähigkeit zu Sprechen‘, oder ‚allgemein akzidentell‘ so wie ‚Bewegung‘, ‚Schwarzheit‘, ‚Weisheit‘.
INTERPRETATION- ANMERKUNGEN
21. War die Re-Lektüre und einsetzende Interpretation von Avicennas Text bis zu dieser Stelle relativ einfach, so zeigen sich jetzt erste Problemstellungen, die man nicht mehr so einfach ‚verworten‘ kann.
22. Einmal gibt es das Phänomen, dass er Begriffe einführt und benutzt, die nicht – zumindest auf einen ersten Blick – direkt erklärbar sind. Dann werden Zusammenhänge thematisiert, wo man sich die Frage stellen kann, ob er dies wirklich ‚gemeint‘ haben kann oder, falls ja, wie man damit umgehen will.
23. Dies gibt Gelegenheit, kurz ein paar Worte zum ‚Interpretieren‘ zu sagen. Ich werde dabei nicht auf die sehr umfangreiche Literatur zu diesem Thema eingehen (im Bereich Philosophie, Literatur und wissenschaftliche Bibelauslegung gibt es dazu nicht hunderte, sondern sicher tausende von Artikeln und Büchern. Einiges davon musste ich zu früheren Zeiten durcharbeiten). Ich beschränke mich hier auf jene Grundprinzipien, die ich hier anwenden möchte.
24. Die philologischen Fragen, ob die englische Übersetzung hier den arabischen Text korrekt wiedergibt, oder ob gar der arabische Text Überlieferungsfehler aufweist, kann ich hier nicht behandeln. Ich muss den Text nehmen, wie ich ihn vorfinde, und wenn sich für mich Unklarheiten ergeben, kann ich sie nur benennen und versuchen sie zu interpretieren.
25. Was die ‚Interpretation‘ (Auslegung, Deutung, …) des Textes angeht, so gibt es ja mindestens zwei verschiedene Ansprüche: (i) man will die ‚Bedeutung‘ rekonstruieren, die der Autor selbst mit dem verknüpft hatte (also eine Art ‚konservierende‘ Interpretation), oder (ii) man will die Bedeutung des Autors (des Textes) in einem anderen/ neuen Bedeutungsrahmen ‚rekonstruieren‘, ihn quasi von Bedeutungsraum R_Autor in den Bedeutungsraum R_Leser ‚übersetzen‘.
26. Beide Vorgehensweisen haben ihr Recht. Die ‚konservierende‘ Rekonstruktion ist idealerweise eigentlich der erste Schritt und die Voraussetzung für die ‚Neuinterpretation‘. Es ist aber eine offene Frage, ob ein Leser immer und überall über genau die Voraussetzungen in seinem Denken verfügt, dass er den ursprünglichen Bedeutungsraum R_Autor überhaupt eins-zu-eins rekonstruieren kann. Nach ca. 1000 Jahren, die uns von Avicenna trennen, ist es sogar ziemlich unwahrscheinlich, dass wir dies überhaupt noch können.
27. Hier, in dieser Rekonstruktion, werde ich erst gar nicht versuchen, den ursprünglichen Bedeutungsraum R_Autor zu rekonstruieren, da ich niemals wüsste, ob ich mit meinen Überlegungen ‚richtig‘ liege oder nicht. Dies Referenzproblem haben alle wissenschaftlichen Rekonstruktionen alter Texte (dies gilt natürlich auch für das hebräische Alte Testament, das griechische Neue Testament und den arabischen Koran).
28. Im weiteren Verlauf werde ich also die bisherigen Rekonstruktionsannahmen weiter verfolgen. Letztlich ist es eine Art ‚Test‘, ob und wie sich der Text von Avicenna in einem modernen erkenntnistheoretischen Modell ’neu lesen‘ lässt.
DISKUSSION
29. Bisher haben wir folgende allgemeine Annahmen bei der Rekonstruktion des Textes von Avicenna getroffen:
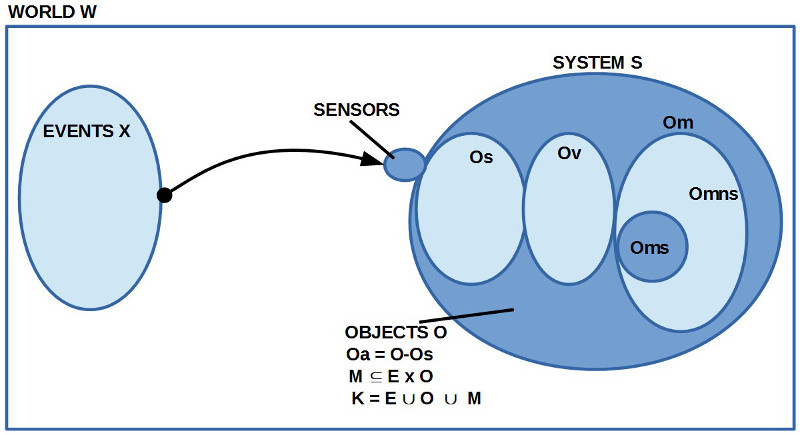
30. Die Ausdruckselemente E einer Sprache L sind nur ‚Zeiger‘, die auf irgendwelche kognitiven Objekte O hindeuten, die im Rahmen der generierten Zeigebeziehung M für die Ausdruckselemente E zu dem werden, was wir ihre Bedeutung nennen.
31. Die kognitiven Objekte O entstehen in einem Erzeugungsprozess, der Eigenschaften X der umgebenden Welt W über sinnliche Wahrnehmungsprozesse perc() und interne Abstraktionsprozesse $latex \alpha$ als irgendwelche Objekte O klassifiziert. Man könnte von daher auch sagen $latex \kappa = perc \otimes \alpha$, oder $latex \kappa(X, O) = O$.
32. Wir hatten ferner noch unterschieden zwischen ‚echten‘ Objekten, d.h. solchen Bündelungen von Objekten, die als solche in der umgebenden Welt W ‚vorkommen‘ und und solchen ‚unechten‘ Objekten, die zwar gebildet werden können, die aber immer nur ‚als Teil anderer Objekte‘ auftreten können. Die Definition von ‚wesentlich universellen Objekten‘ von Avicenna deckt sich mit dem Konzept ‚echter Objekte‘ und Avcennas Definition von ‚akzidentellen universellen‘ Objekten deckt sich mit den unechten Objekten, die anderen Objekten zukommen können, aber nicht müssen.
DISKUSSION – KATEGORIEN
33. Avicenna führt dann indirekt das Konzept von ‚(wesentlichen universellen) Kategorien‘ ein, die ich indirekt rekonstruiert habe als solche ‚wesentlich universellen Objekte‘, ‚über die‘ es keine weiteren Verallgemeinerungen mehr gibt. Da er es nur bei einzelnen Beispielen belässt ohne wirkliche Argumentationen bleibt hier einiges offen.
34. Die genannten drei Kategorien erscheinen wie eine Art ‚Meta-Klassifikation‘ über allen möglichen Objekten, so eine Art ‚Typisierung‘ der verschiedenen möglichen Objektbildungen. Versucht man im Bereich der Objektklassifikationen kriterien zu finden, welches Objekt zu welcher Kategorie gehört, wird es aber schnell schwierig.
35. Kategorie ‚Substanz‘: Wann ist ein Objekt eine ‚Substanz‘ und wann ‚Qualität‘ oder ‚Quantität‘? Ein erster Ansatzpunkt wäre zu sagen, dass alle ‚echten‘ Objekte ‚Substanzen‘ sind und alle ‚unechten‘ Objekte ‚Qualitäten‘. Was aber wäre dann mit den ‚Quantitäten‘? Die ‚Anzahl‘ von Objekten (echten wie unechten) ist ja keine ‚Eigenschaft an sich‘, sondern ist eher eine ‚Metaeigenschaft‘, die man vorhandenen (real oder gedachten) Objekten zuordnen kann. Im Vergleich zu Farben, Formen, Tönen usw., die auf Sinneseigenschaften aufsetzen, ist ‚Quantität‘ als Metaeigenschaft eine abgeleitete, sekundäre, abstrakte Eigenschaft, so wie z.B. auch ‚größer/ kleiner‘, ‚vorher/ nachher‘, ‚vorne/ hinten, ‚oben/ unten‘, usw. In allen genannten Fällen gibt es schon irgendwelche Objekte, zwischen denen räumliche, zeitliche – oder sonstige – allgemeine Beziehungen erkennbar sind. Diese indirekten, sekundären, abgeleiteten Beziehungen bilden dann eine eigene Klasse von ‚abstrakten‘ Eigenschaften, von denen die ‚Quantitäten‘ nur eine Teilmenge wären. Wenn also Avicenna schon die Kategorie ‚Quantität‘ bemüht, warum nicht auch ‚Raum‘ und ‚Zeit‘?
36. Alle diese Überlegungen zu ‚Kategorien‘ als zusätzliche Meta-Klassifikationen der generierbaren Objekte setzen allerdings voraus, dass es möglich ist, im Bereich der Objekthierarchie für alle Objekte O solche ‚Kontexte‘ annehmen zu können, durch die sie bzgl. ‚Substanz‘, ‚Qualität‘, ‚Quantität‘, ‚Raum‘ und ‚Zeit‘ charakterisierbar werden. Im bisher verfolgten Modell würde dies bedeuten, dass Objekte nicht nur über ihre ‚direkten‘ sensorischen Eigenschaften $latex K_{s}$ generiert werden, sondern sie werden von vornherein auch mit minimalen ‚Raumanteilen‘ bzw. in bestimmten ‚Abfolgen‘ ‚gespeichert‘ bzw. sind sensitiv bzgl. Abfolgen ‚erinnerbar‘.
DENKEN ALS KOGNITIVE EVOLUTION
37. Oder, wenn schon, dann noch allgemeiner: der gesamte Objekterzeugungsprozess $latex \kappa$ mus so beschaffen sein, dass er die fundamentalen Eigenschaften X der umgebenden Welt so in die Objekthierarchie übersetzt, dass (i) echte und unechte Objekteigenschaften hinreichend erhalten bleiben können, dass (ii) räumliche und zeitliche Verhältnisse hinreichend repräsentiert werden können, dass (iii) quantitative Verhältnisse erzeugt werden können (z.B. Aufzählungen und Äquivalenzklassen), dass (iv) neben den Eigenschaften, die ‚gegeben‘ sind (IST, real), auch ’neue‘ Kombinationen erzeugt werden können (Möglichkeit, Potenz, kombinatorischer Raum), und dass (v) neue Kombinationen (Möglichkeiten) mit dem ‚realen Raum‘ verglichen werden können.
38. Sofern dies möglich ist (und alles, was wir über das menschliche Denken heute wissen, bestätigt dies), kann man dann diese Art von Denken als Fortsetzung der biologischen Evolution im Bereich des Denkens (quasi als kognitive Evolution) betrachten, d.h. die biologische Evolution hat – mit ihrem kombinatorischen genetischen Mechanismus – Strukturen geschaffen (Körper mit Gehirn), die in der Lage sind, die an die materiellen Strukturen gebundene Kombinatorik neuer Lebensformen über die Neuronennetze zu dynamisieren, zu beschleunigen, zu flexibilisieren. Mit der Kombinatorik des neuronalen Denkens konnte die biologische Evolution der Entwicklung neuer, leistungsfähigerer Lebensformen einen gewaltigen Schub im einzelnen Organismus verleihen; durch die Möglichkeit symbolischer Kombination können sich die neurologisch erzeugbaren neuen Denkräume zusätzlich direkt miteinander verschränken und die Entwicklung neuer Lebensformen in bis dahin ungeahnte Dimensionen katapultieren.
39. Doch zurück zur vorliegenden Interpretationsaufgabe.
GENUS – SPEZIES
40. Bislang haben wir ansatzweise eine Rekonstruktion des Konzeptes von ‚Kategorien‘ als Meta-Klassifikationen im Bereich der dynamischen Objekthierarchie.
41. Unklar, da widersprüchlich, bleibt bei Avicenna die Verwendung der Begriffe ‚Genus‘ und Spezies‘. Eine erste, einfache, und nachvollziehbare Interpretation wäre die, jedes Objekt als ein ‚Genus‘ zu bezeichnen, das ‚Instanzen‘ besitzt, denen ‚differenzierende‘ Eigenschaften zukommen (wie auch die verschiedenen Genus-Objekte sich voneinander durch Eigenschaften unterscheiden). ‚Spezies‘ wären dann jene voneinander abgrenzbaren Instanzen (vgl. auch Carl von Linné (1707 – 1778), sein Werk ‚Systema Naturae‘), die einem Genus ‚untergeordnet‘ wären. Allerdings kommen die Begriffe ‚Genus‘ und ‚Spezies‘ im Text mehrfach in Verwendungen vor (z.B. auch als ‚Spezies der Spezies‘), die sich – aus meiner Sicht – einer schlüssigen Interpretation entziehen.
ALLGEMEINE UND SPEZIELLE AKZIDENZ
42. Mit den Begriffen ‚allgemeine‘ und ’speziellen‘ Akzidenzien verhält es sich ähnlich: es gäbe eine einfache, nachvollziehbare Interpretation, aber diese deckt nicht alle Verwendungsweisen dieser Begriffe ab.
43. Ausgangspunkt sind ja nicht-zusammengesetzte Ausdrücke mit einer universellen Bedeutung, bei der zwischen ‚wesentlichen‘ und ‚akzidentellen‘ unterschieden wurde. Die ‚akzidentellen universellen Begriffe wurden zuvor schon als ‚unechte Objekte‘ rekonstruiert, die niemals isoliert auftreten können, sondern immer nur als Teile von echten (wesentlichen universellen) Objekten. Insofern sind sie ‚akzidentell‘ und eine informelle abkürzende Redeweise könnte sie als ‚Akzidentien‘ bezeichnen, verstanden als Eigenschaften, die bei einem Objekt auftreten können, aber nicht müssen.
44. Wäre zu klären, was ‚allgemeine‘ von ’speziellen‘ Akzidenzien unterscheidet. Hier nochmals die Beispiele aus dem Text, wonach ‚fest‘ (engl.: ’solid‘) allgemeiner sei als ‚Lebewesen‘, aber spezieller als ‚Substanz‘; entsprechend dass ‚Zahl‘ allgemeiner sei als ‚gleich‘ (engl.: ‚even‘), aber spezieller als ‚Quantität‘, und schließlich dass ‚Gleichheit (engl.: ‚eveness‘) allgemeiner sei als ‚vier‘, doch spezieller als ‚Quantität‘.
45. Die Eigenschaft ‚fest‘ ist nach bisheriger Rekonstruktion klar ein unechtes Objekt, d.h. eine akzidentelle Eigenschaft, die als Teil von echten Objekten auftreten kann. Zu sagen, dass diese akzidentelle Eigenschaft allgemeiner sei als ‚Lebewesen‘, aber spezieller als ‚Substanz‘, macht nicht unbedingt Sinn, genauso wenig wie es Sinn machen würde, Hühner mit Grashalmen zu vergleichen. Es sei denn, es gäbe einen ‚übergreifenden Aspekt‘, auf den sich beide, die Hühner und die Grashalme, beziehen lassen würden.
46. Ich kann in diesem Zusammenhang keinen solchen übergreifenden Gesichtspunkt erkennen. Bestimmte akzidentelle Eigenschaften können bei Objekten auf verschiedenen Stufen der Objekthierarchie auftreten. Hier ein Beziehungsgeflecht zwischen den Eigenschaften konstruieren zu wollen überzeugt mich nicht.
ALLGEMEINE EINSCHÄTZUNG
47. Schon an dieser Stelle der Relektüre von Avicennas Logik deutet es sich an, dass Avicenna viele seiner technischen Begriffe nur unzulänglich erklärt und voneinander abgrenzt. Ein Grund dafür kann sein, dass er die das Konzept der Objekterstehung und der Objekthierarchie als Gegenpol zu den Ausdrücken offenbar nicht als eigenständiges System systematisch entwickelt. In anderen Interpretationsprojekten (z.B. bei Nicolai Hartmann) musste ich die Rekonstruktion irgendwann einfach abbrechen, da der Text in sich irgendwann so widersprüchlich war, dass ein sinnvolles Weiterlesen nicht mehr möglich erschien.
Fortsetzung folgt …
QUELLEN
- Avicenna, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
- Digital Averroes Research Environment
- Stanford Encyclopedia of Philosophy, Aristotle’s Logic
- Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
- Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
- Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
- Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7
Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER.