(Letzte Änderung: 3.Oktober 2014, 08:47h)

VORGESCHICHTE

Für einen Überblick zu allen vorausgehenden Beiträgen dieser rekonstruierenden Lektüre von Avicennas Beitrag zur Logik siehe AVICENNAS ABHANDLUNG ZUR LOGIK – BLITZÜBERSICHT.

1. Bei der Beschreibung der ‚Bedeutung‘ der logischen Ausdrücke in einer syllogistischen Figur wurde im letzten Beitrag Gebrauch gemacht von Diagrammen, in denen ‚Kreise‘ ‚Mengen‘ repräsentieren und die Anordnung der Kreise ‚Mengenverhältnisse‘.

2. Diese Vorgehensweise ist nicht neu und wird vielfach benutzt. Am bekanntesten ist wohl der Begriff ‚Venn-Diagramm‘.

3. So bekannt die Methode von verdeutlichenden Mengendiagrammen einerseits ist, so wenig tragen diese Methoden bislang zum wirklichen Verständnis des Gesamtzusammenhanges bei. Uns interessiert ja hier der Mensch als ’semiotisches System‘, als ein ‚adaptives Input-Output-System‘, das sowohl Objektstrukturen $latex perc(X,W)=I, O \subseteq I$ aus der umgebenden Welt W wahrnehmen kann wie auch – von den Objekten unterschiedene – Ausdrucksstrukturen $latex perc(X,W)=I, E \subseteq I$, die sich auf die Objektstrukturen beziehen können.

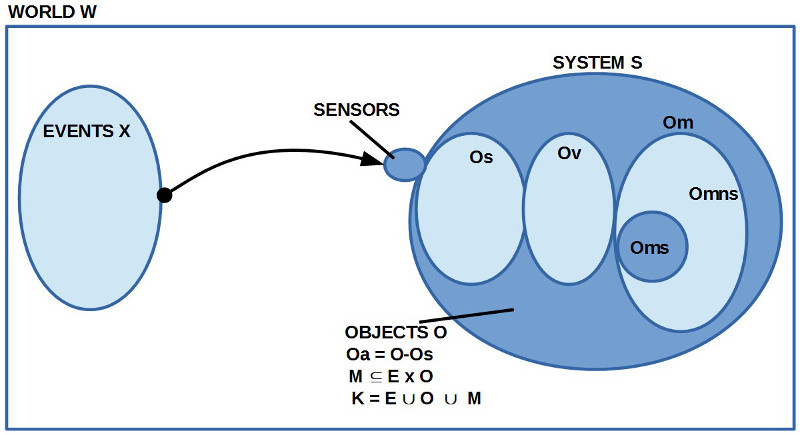
4. Entsprechend der Begriffe, die in Teil 14b eingeführt worden sind (und dann in den nachfolgenden Beiträgen weiter differenziert wurden), bilden die Objekte O eine dynamische Hierarchie mit impliziten Raum-, Zeit- und Anzahlstrukturen, angereichert mit diversen Beziehungen innerhalb dieser Strukturen. Wenn wir von der ‚Bedeutung‘ M der logischen Ausdrücke E – also M(E) — sprechen wollen, dann müssen wir diese gesamte dynamische Objektstruktur ins Auge fassen. Man wird zwar erwarten, dass sich die Strukturen, die in Mengendiagrammen verdeutlicht werden, in der dynamischen Objektstruktur ‚wiederfinden‘, aber man muss in einzelnen konkreten Schritten (‚konstruktiv‘) aufzeigen, wie dies gehen könnte.

FIGUR 1 MIT DEN QUANTOREN AAA

5. Betrachten wir die Struktur des ersten Syllogismus mit der Quantorenkombination (A F B), (A B H) und (A F H).

6. Wenn gesagt wird, dass ‚Alle F sind B‘ und ‚Alle B sind H‘, dann handelt es sich bei dem Quantor ‚Alle‘ um einen ‚Anzahlquantor‘, der sich auf Objekte bezieht, die entsprechend Elemente enthalten, über die man solche Aussagen machen kann. Nach der bisherigen Analyse geht dies nur, wenn sich die Ausdrücke ‚F‘, ‚B‘ und ‚H‘ auf ‚echte Objekte‘ aus Oa beziehen. Die Menge der ‚Elemente‘ eines echten Objektes kann man in der Tat mittels eines ‚Kreises‘ ‚modellieren‘ in dem Sinne, dass die Kreisfläche alle Elemente symbolisiert, die zum echten Objekt gehören.

7. Da wir es im ersten Beispiel (A F B), (A B H) und (A F H) ausschließlich mit echten Objekten zu tun haben, könnten wir für jedes dieser Objekte ein Kreismodell benutzen.

8. Die Aussagen (A F sind B), (A B sind H) und (A F sind H) stellen jeweils (i) eine Beziehung zwischen den Elementen von zwei Mengen her und (ii) machen Angaben zu der Anzahl; in diesem Fall ‚Alle‘.

9. Grundsätzlich gibt es folgende Möglichkeiten: ELEMENTSCHAFT: (i) Ein Element x aus einer Menge A ist auch Element von einer anderen Menge B oder (ii) eben nicht. Zusätzlich gibt es die ANZAHL: (iii) Die festgestellte Elementschaft trifft auf ‚Alle‘ Elemente zu oder (iv) ’nicht‘ auf ‚alle‘, d.h. ‚einige‘. Oder (v) ‚Für Alle nicht‘, also ‚keine‘.
10. Benutzt man das Kreismodell, dann kann man die Elementschaftsbeziehung eines Elementes x dadurch ausdrücken, dass man x ‚in‘ einem Kreis notiert oder ‚außerhalb‘.

11. Die Anzahlbeziehung könnte man dann grundsätzlich so ausdrücken, dass (i) bei ‚Allen‘ Elementen alle Elemente eines Objektes A auch im Objekt B sind, d.h. die beiden Kreise überdecken sich vollständig. Bei (ii) ‚Nicht Alle = Einige‘ gibt es Elemente eines Objektes A, die auch im Objekt B sind, aber nicht alle. In diesem Fall würden sich im Kreismodell die beiden Kreise A und B teilweise überdecken/ überlappen. (iii) Bei einer Aussage wie ‚Einige A sind nicht B‘ ist zwar klar, dass einige Elemente von A definitiv nicht in B sind, aber was weiß man von den anderen Elementen von A? Kann man zwingend davon ausgehen, dass diese dann in B sind? Denkbar wäre, dass alle anderen Elemente von A, die nicht in B sind zu einer anderen Menge C gehören und man nur darauf hinweisen wollte, dass einige mit Blick auf B nicht in B seien. Insofern wäre eine Aussage wie ‚Einige A sind nicht B‘ zunächst ‚unterbestimmt’/ ’nicht vollständig definiert‘, solange man keine speziellen Verabredungen trifft. Schließlich (iv) hat man noch den Fall ‚Alle A sind nicht B‘. Dies ist wieder eindeutig. Fasst man alle Elemente außerhalb von B als das ‚Komplement von B‘ ($latex \overline{B}$) auf, dann kann man sagen, dass alle Elemente von A in dem Komplement sind; keines ist in B.

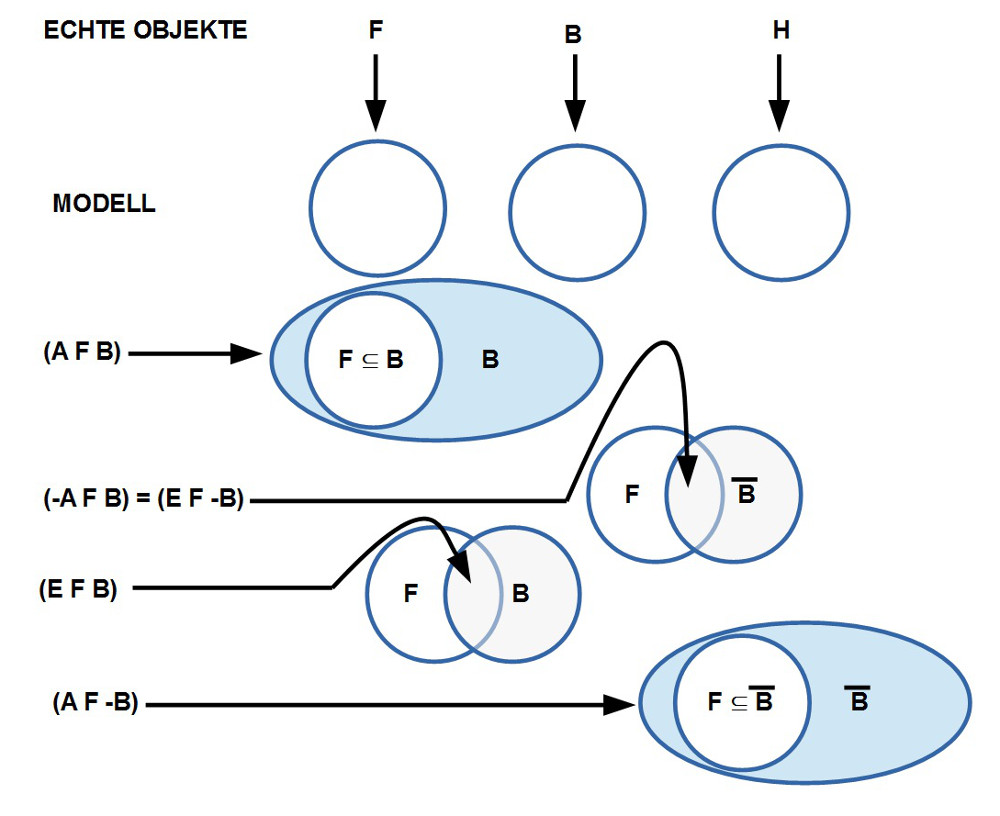
12. Grafisch sieht dies so aus (siehe Diagramm): (i) zwei Kreise sich entweder vollständig überlappen (zwei Objekte sind ‚identisch gleich‘) – was im Beispiel nicht vorkommt –, oder (ii) ein Kreis ist völlig in einen anderen eingebettet (ein Objekt ist eine Teilmenge von einem anderen), oder (iii) zwei Kreise überschneiden sich partiell, oder (iv) zwei Kreise sind völlig voneinander getrennt (was man alternativ auch so ausdrücken kann, dass der eine Kreis eine Teilmenge des Komplements des anderen Kreises ist.

13. Während sich der explizite Bezug eines Objektes A zu einem Objekt B konkret und konstruktiv darstellen lässt, zeigen sich im Falle von ‚Komplementbildungen‘ (siehe Diagramm) Probleme. Die rein grafische Modellierung erlaubt keine klare Zuordnung von zwei Komplementen. Dazu bräuchte man zusätzliche Informationen. Diese könnte man z.B. durch explizite Aufstellung von ‚Axiomen‘ gewinnen. Will man aber die ‚Logik des tatsächlichen Sprachgebrauchs‘ nicht ‚verbiegen‘, muss man zuvor die Frage stellen, ob sich Anhaltspunkte aus dem dynamischen Objektmodell gewinnen lassen.

14. Nimmt man beispielsweise an, dass das dynamische Objektmodell ein ‚bottom-up‘ Modell ist, das seinen Ausgang bei konkreten, endlichen Wahrnehmungsereignissen Os nimmt, die mittels einer vorgegebenen Verarbeitungsmaschinerie (Gehirn, Algorithmus) in eine abstrakte Struktur von Objektebenen übersetzt werden, dann würde man vermuten, dass diese Maschinerie grundsätzlich von endlichen Mengen ausgeht, deren Informationsgehalt durch entsprechende Operationen ‚ausgewertet‘ wird. Die Bildung von – quasi ‚unendlichen‘ – ‚Komplementen‘ zu endlichen Strukturen ist dann zwar als Operation definierbar, aber wäre nur erklärt für den ‚endlichen Anteil‘. Das ‚Verhalten im quasi Unendlichen‘ wäre nicht wirklich definiert; es würde dann zwar ‚begrifflich existieren‘, aber wäre ‚praktisch nicht nutzbar‘. Letzteres wäre auch ’systemgefährdend‘, da die Annahme von Elementen in einem nur abstrakt konstruierbaren ‚unendlichen Raum‘ schnell in ‚Gefahrenzonen‘ führen kann.

15. Würde man dies die ‚generelle Endlichkeitsannahme‘ [GenEndl] nennen, dann wäre dies eine Art ‚Meta-Axiom‘, mit dem man die verschiedenen logischen Beziehungen als ‚zulässig‘ oder ’nicht zulässig‘ qualifizieren könnte [Mit dem philosophischen Konstruktivismus hat diese Endlichkeitsthese hier nur bedingt etwas zu tun].

ECHTE OBJEKTE und VERERBUNG

16. Es wurde oben schon festgestellt, dass die in der ersten Figur zugrunde liegende Annahme bzgl. der Art der Objekte in der Rekonstruktion dieses Blogs ‚echte Objekte‘ sein müssen, also Objektrepräsentationen, in denen Objekte repräsentiert werden, die echte Eigenschaften haben und denen man aufgrund dieser Charakterisierung andere Eigenschaftsvorkommnisse als Elemente zuordnen kann. Ferner gilt in dieser Rekonstruktion, dass die dynamische Objektstruktur automatisch auch Raum und Zeit bereitstellt sowie eine Vielzahl von impliziten Beziehungen.

17. Wenn nun das Schema sagt ‚Alle F sind B‘ und ‚Alle B sind H‘ gefolgt von ‚Alle F sind H‘, dann haben wir drei echte Objekte F, B und H, die so beschaffen sein müssen, dass man über die potentiellen Elemente dieser echten Objekte reden kann.

18. In der dynamischen Objekthierachie O werden ‚echte Objekte‘ im Bereich O – Os primär über ihr ‚Objektprofil‘ repräsentiert (eine Menge charakteristischer Eigenschaften) ergänzt um eine endliche Menge von ‚Beispielen‘. Sei P_F das Profil für echte Objekte der Art F, P_B und P_H entsprechend die Profile für die Objektmengen B und H.

19. Zu sagen, dass ‚Alle F sind B‘ würde dann bedeuten, dass alle charakterisierenden Eigenschaften des Objektprofils P_F auch im Objektprofil von P_B vorkommen. Dies würde gelten, unabhängig davon, wie viele ‚reale‘ Elemente beide echten Objekte tatsächlich enthalten! Man könnte daher auch direkt hinschreiben $latex P_{F} \subseteq P_{B}, P_{B} \subseteq P_{H}, P_{F} \subseteq P_{H} $. Hier zeigt sich eine ‚transitive‘ Beziehung des Enthaltenseins.

20. Das Auftreten von drei echten Objekten in einer syllogistischen Schlussfigur stellt allerdings – gemessen am alltäglichen Denken – eine Art Spezialfall dar. In vielen – den meisten ? — Fällen setzen wir nicht echte Objekte alleine in Beziehung sondern betten echte Objekte ein in Veränderungsbeziehungen wie z.B. ‚Hans schaut Sonja an‘, ‚Die Sonne geht gerade auf‘, ‚Das berühmte rote Auto biegt um die Ecke‘, ‚Alle Nachbarn von Sonja sehen das rote Auto‘, ‚Hans ist ein Nachbar von Sonja‘, usw.

21. In solchen Sätzen nach dem Schema ‚S P‘ repräsentiert das Prädikat P dann eben die Veränderung und mögliche Begleitumstände.

22. Setzen wir F= ‚Die Nachbarn von Sonja‘ und ‚B1= ‚Das rote Auto‘, dann können wir schreiben (A F sehen B1). Setzen wir H1= ‚Hans‘, dann können wir schreiben (– H1 ist F). Da der Ausdruck ’sehen‘ keine ‚Enthaltensbeziehung‘ repräsentiert, sondern eine bestimmte Form von Aktivität, liegt keine mögliche Enthaltensbeziehung zwischen F und B1 vor. Wohl aber zwischen F und H1 im Sinne von $latex B1 \in F$. Dann kann man fragen, ob die Aktivität, die für ‚Alle F‘ gilt, damit auch für H1 gilt, da H1 ja ein Element von F ist. Von der Grundstruktur her würde unser Denken dies bejahen; wir denken einfach so. Also folgern wir ‚automatisch‘ (– H1 sieht B1).

23. Dies bedeutet, wenn es Profile von echten Objekten gibt, denen zusätzliche Eigenschaften zugeordnet werden – z.B. Aktivitäten –, dann wird gefolgert dass die zugeordneten Aktivitäten auf alle Elemente des Profils ‚übertragen‘ werden, oder, anders formuliert, alle Elemente eines Profils P eines echten Objektes ‚erben‘ die zugesprochenen Eigenschaften. Wenn ‚Alle‘ Elemente dieser Eigenschaften haben, dann erben alle, wenn ‚Nicht Alle‘, also ‚Einige‘, dann erben nur einige, oder ‚Alle nicht‘, dann erbt ‚Kein‘ Element.

24. Über die ‚Enthaltensbeziehung‘ (wie ‚ist‘, ’sind’…) werden also quasi ‚Vererbungsverhältnisse‘ repräsentiert. Über ‚Aktivitätszuweisungen‘ (‚läuft‘, ’spricht‘ …) werden zusätzliche ‚Eigenschaften‘ (‚unechte Objekte‘) repräsentiert, die für ausgewählte Elemente eines echten Objekts gelten.

QUANTORENVIELFALT

25. Betrachtet man alle Quantorenkombinationen der syllogistischen Muster, dann stellt man fest, dass es sich ausschließlich um ‚Anzahlquantoren‘ handelt, also Quantoren, die sich auf die potentiellen Elemente eines echten Objekts beziehen. ‚Potentielle Element‘, da diese Anzahlquantoren sich – wie gesagt – auf die Eigenschaften des Profils eines echten Objektes beziehen, mittels deren potentielle Elemente bestimmt werden, nicht auf die tatsächlichen Elemente.

26. In der dynamischen Objektstruktur gibt es aber auch ‚Raum-‚ und ‚Zeit-Quantoren‘.Warum kommen diese in den syllogistischen Mustern nicht vor? Die Beschränkung auf Anzahlquantoren stellt somit eine weitere starke Einschränkung dar.

27. Würde man sagen ‚Immer geht nach X Stunden wieder die Sonne auf‘, ‚X Stunden sind seit dem letzten Sonnenaufgang vergangen‘, dann könnte man daraus folgern, ‚jetzt wird die Sonne aufgehen‘. Setzt man eine Zeitachse mit Zeitpunkten voraus, für die mit ‚Immer = Zu allen Zeitpunkten = At‘ gesagt wird, dass eine Eigenschaft ‚F1=die Sonne‘ ‚geht auf‘ sich nach einem festen Abschnitt von ‚X Stunden‘ gesagt wird, dass sich diese Eigenschaft ‚wiederholt, also (At ‚X Stunden‘ geht auf F1), (Jetzt ist ‚X Stunden‘), (‚Jetzt ‚geht auf‘ F1). Implizit hat man hier auch die Struktur von echten Objekten (‚die Sonne‘) mit zugeordneten Eigenschaften ‚geht auf‘ bzw. den Zeitobjekten ‚Jetzt‘, ’10 Stunden‘.

28. Entsprechend kann man die Frage nach den Raum-Quantoren stellen. warum werden diese ausgeklammert? ‚Überall brennt die Sonne‘, ‚Hans wohnt in Berlin‘, ‚In Berlin brennt die Sonne‘. ‚Überall = An allen Orten = Ar‘, F1=’die Sonne‘, B1=’Hans‘, Berlin ist ein Ort, (Ar Orte brennt F1), (H1 wohnen Berlin), und über ‚Vererbung der Eigenschaft von allen Orten erbt der Ort Berlin die Eigenschaft (Berlin brennt F1).

OBJEKTIFIZIERUNG, ENTHALTENSEIN, ZUSCHREIBUNG, VERERBUNG

29. Aus den bisherigen Überlegungen lassen sich die Umrisse einer möglichen ‚Logik‘ auf der Basis einer ‚dynamischen Objektstruktur‘ erkennen.

30. Basis für alles andere sind ‚Objektifizierungen‘ von Eigenschaftsdimensionen wie ‚echte Objekte‘, ‚Raumgebiete‘ und ‚Zeitachse‘.

31. Zwischen echten Objekten, Raumpunkten und Zeitpunkten kann es ‚Enthaltensbeziehungen‘ geben. Z.B. (i) Von den Profileigenschaften von zwei echten Objekten A und B kann man sagen, dass ‚Alle‘ oder ‚Nicht Alle = Einige‘ oder ‚Alle nicht = Kein‘ Element von A auch Element von B ist. (ii) Die Wohnung von Hans ist Teil des Gebäudes X. Das Gebäude X gehört zum Ort Y…. (iii) Der 5.Oktober 1948 gehört schon zum Nachkriegsdeutschland. Nachkriegsdeutschland ist Teil des 20.Jahrhunderts. Das 20.Jahrhundert gehört zur Periode des homo sapiens.

32. Sofern Objektifizierungen angegeben sind, kann man diesen diverse Eigenschaften zuweisen (Das Auto ist rot; Die Nachbarn von Sonja sehen das rote Auto; die Sonne geht alle X Stunden auf; …)

33. Wenn man Objekten Eigenschaften zugeschrieben hat, dann kann man diese Eigenschafte ‚übertragen’/ ‚vererben‘ auf alle Elemente, die in dem betreffenden Objekt ‚enthalten sind‘. Wenn es zu allen Zeiten Kriege gab, dann gibt es auch zum aktuellen Zeitpunkt einen Krieg; wenn überall die Sonne scheint, dann auch dort, wo man ist; Wenn alle Menschen Lebewesen sind und von Lebewesen gesagt wird, dass sie sterben, dann sterben auch die Menschen.

Fortsetzung folgt

QUELLEN

• Avicenna, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
• Digital Averroes Research Environment
• Immanuel Kant, Critik der reinen Vernunft‘, Riga, 1781
• Konrad Lorenz, 1973, ‚Die Rückseite des Spiegels. Versuch einer Naturgeschichte des menschlichen Erkennens‘, München, Zürich: Piper
• Nicholas Rescher (1928 – ),The Development of Arabic Logic. University of Pittsburgh Press, 1964
• Hans-Jörg Sandkühler (Hg.) unter Mitwirkung von Dagmar Borchers, Arnim Regenbogen, Volker Schürmann und Pirmin Stekeler-Weithofer, ‚Enzyklopädie Philosophie‘, 3 Bd., Hamburg: FELIX MEINER VERLAG, 2010 (mit CD-ROM)
• Stanford Encyclopedia of Philosophy, Aristotle’s Logic
• Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
• Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
• Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
• Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7

Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER