Archiv der Kategorie: Avicenna

AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 22

Allquantor, Analytisch, Aristoteles, Avicenna, Beweis - logischer, Logik, Logik - Alltag, Logik - Antike, Logik - formale, Schlussfigur, Schlussfolgern, Syllogismus - Konjunktiver

(Letzte Änderungen: Mi 15.Okt.2014, 12:17h)

VORGESCHICHTE
Für einen Überblick zu allen vorausgehenden Beiträgen dieser rekonstruierenden Lektüre von Avicennas Beitrag zur Logik siehe AVICENNAS ABHANDLUNG ZUR LOGIK – BLITZÜBERSICHT.

1. Im letzten Beitrag entstand die Arbeitshypothese, dass aufgrund des ‚fließenden‘ Bedeutungsübergangs zwischen ‚echten‘ und ‚unechten‘ Objekten auf der Bedeutungsseite damit die Unterscheidung zwischen ‚Subjekt‘ (S) und ‚Prädikat‘ (P) auch fließend würde. Das würde die Unterscheidung ob die Terme ‚S‘ oder ‚P‘ sind aufheben. Anders ausgedrückt, die Terme in einer Schlussfigur erscheinen ‚invariant‘ bzgl. der Kategorisierung als ‚S‘ oder ‚P‘.

2. Verfolgt man den Gedanken der ‚Invarianz‘ weiter, dann sieht man sofort, dass die Anordnung der Prämissen 1 und 2 auch ‚invariant‘ ist gegenüber ‚Vertauschung‘. Hat man die Prämissen A1: (_ F M) und A2: (_M H) mit dem Muster, das die Schlussfigur 1 charakterisiert, dann erhält man durch Vertauschen der Reihenfolge A1: (_ M F) und A2: (_H M) die Schlussfigur 4 (die Avicenna nicht benutzt), und kann feststellen, dass diese Vertauschung nichts an der Bedeutungsstruktur und damit an der Folgerung ändert. Darüber hinaus sieht man, dass durch die Vertauschung der Prämissen auch die Quantoren der ersten und zweiten Prämisse gespiegelt wurden. Der ‚Wahrheitsgehalt‘ der Schlussfigur bleibt ‚erhalten‘.

Schlussfigur 1 mit Quantorenkombination 1-4 'gespiegelt' als Schlussfigur 4 mit Quantorenkombination 1-4, ebenfalls gespiegelt
Schlussfigur 1 mit Quantorenkombination 1-4 ‚gespiegelt‘ als Schlussfigur 4 mit Quantorenkombination 1-4, ebenfalls gespiegelt

3. Es lieg nahe, den ‚Spiegelungstest‘ auch mit den Schlussfiguren 2 und 3 vorzunehmen. Hier die Ergebnisse:

Alle Muster von Figur 2 samt inverse
Alle Muster von Figur 2 samt inverse
Alle Muster von Figur 3 samt Inverse
Alle Muster von Figur 3 samt Inverse

4. Man sieht, dass die Spiegelung in Form der Veränderung der ‚Abfolge‘ der Prämissen keine Wirkung auf den ‚Wahrheitsgehalt‘ besitzt. Dies wird verständlich, wenn man sich klar macht, dass die ‚Ausdrücke‘ E einer Sprache L ja nicht die ‚Bedeutung selbst‘ darstellen, sondern nur auf die Bedeutungsstrukturen ‚Bezug nehmen‘. Wie immer diese beschaffen sein mögen, die sprachlichen Strukturen ‚kodieren‘ diese nur. Und insoweit es sich bei den hier angesprochenen Sachverhalten um statische Beziehungsverhältnisse handelt, spielt die Abfolge der beschreibenden Äußerungen – zumindest in diesen Fällen — keine Rolle.

5. Fasst man alle Schlussfiguren (ohne ihre ‚bedeutungsgleichen‘ inversen Varianten) zusammen, dann erhält man folgende Tabelle:

Tabellarische Gesamtübersicht über alle Schlussfiguren 1-3 samt allen benutzten Quantorenkombinationen 1-11
Tabellarische Gesamtübersicht über alle Schlussfiguren 1-3 samt allen benutzten Quantorenkombinationen 1-11

6. Angesichts dieser vielen ‚Invarianzen‘ drängt sich verstärkt die Frage auf, was denn dann der ‚harte Kern‘ an Strukturen ist, an denen sich der ‚Wahrheitsgehalt‘ einer Folgerung orientiert.

7. Bislang hat sich schon herausgeschält, dass es um ‚Beziehungen zwischen Mengen‘ geht (welche Elemente in welchen Mengen vorkommen), und um Eigenschaften, die diesen Elementen ‚zugesprochen‘ werden.

8. Die Schlussfiguren 1-3 (bzw. 1-4) setzen in den Prämissen genau drei verschiedene Mengen F, H und M voraus, zwischen denen jeweils F und H eine Beziehung zu M haben. Insofern ist M der ‚Mittelterm‘ (und F und H sind die ‚äußeren‘ Terme). Gefragt wird dann immer nach der sich daraus resultierenden Beziehung zwischen F und H. Die ‚Antwort‘ auf diese Frage wird als ‚Schlussfolgerung‘ präsentiert. Das folgende Bild zeigt die Verteilung der Quantoren für alle Schlusfiguren samt ihren Inversen.

Gesamtübersicht Schlussfiguren 1-3 samt ihren Inversen und die Verteilung der Quantoren für jede Schlussfigur
Gesamtübersicht Schlussfiguren 1-3 samt ihren Inversen und die Verteilung der Quantoren für jede Schlussfigur

9. Man kann in dieser Darstellung schon sehen, dass es im Falle der Schlussfiguren 2 und 3 gar keine Spiegelung vergleichbar zu Figur 1 mit der Figur 4 gibt.

10. Betrachtet man nochmals Figur 1, dann kann man folgende Sachverhalte erkennen (siehe Bild): (i) Bei den Mengenverhältnissen gibt es eigentlich nur drei Fälle (A), (E) = (E-), sowie (A-). Zu jedem dieser drei Fälle für Prämisse 1 kann es dann wiederum kombinatorisch jeweils drei Fälle geben. Spielt man diese durch (das Bild zeigt dies nur für den Fall (A F M) in Prämisse 1), dann zeigt sich (ii) dass von den theoretisch möglichen Fällen 3 x 3 = 9 nur jeweils 3 x 2 = 6 geben kann. Dies ergibt sich daraus, dass eine Kombination von E und E bei dem Muster von Figur 1 zu keinem eindeutigen Schluss führt. Ein Partikularquantor E kann hier immer nur zusammen mit einem Allquantor A auftreten.

Systematik der Mengenverhältnisse am Beispiel von Figur 1
Systematik der Mengenverhältnisse am Beispiel von Figur 1

11. Es fragt sich, wieweit diese Überlegungen auch auf die anderen Schlussfiguren übertragbar sind. Im folgenden Bild sind nochmals alle formal möglichen Quantorenkombinationen für jede Schlussfigur aufgelistet mit der Legende: ‚1‘ := wird von Avicenna genannt, ‚?‘ := unbestimmt, ‚+‘ := würde einen Schluss zulassen:

Syllogismen Figuren 1-3, volle Quantorenverteilung
Syllogismen Figuren 1-3, volle Quantorenverteilung

12. In der Tabelle kann man erkennen, dass es neben den Einsen ‚1‘, die anzeigen, dass diese Quantorenkombinationen in den drei ‚Schlussfiguren Verwendung finden, bei allen Schlussfiguren Fragezeichen ‚?‘ gibt, aber auch Pluszeichen ‚+‘. Dies würde bedeuten, dass es weitere mögliche Schlüsse gäbe, die aber von Avicenna nicht genannt werden.

13. Die Klassifikation ‚?‘ bzw. ‚+‘ habe ich spontan vorgenommen, ‚intuitiv‘. Es fragt sich, ob diese ‚intuitive‘ Zuordnung ‚richtig‘ ist, Eine Antwort auf diese Frage setzt voraus, dass man irgendwelche ‚Kriterien‘ explizit machen kann, anhand deren man die ‚intuitive‘ Klassifikation explizit ‚begründen‘ oder ‚widerlegen‘ kann. Dies soll hier versucht werden.

14. Aus der Geschichte der modernen Logik sind zahlreiche formale Kalküle bekannt, deren ‚Wahrheitsfähigkeit‘
nachgewiesen worden ist. Im vorliegenden Fall wird die Frage aber in einem spezifischen Kontext gestellt: (i) wir setzten hier – versuchsweise — eine allgemeine Bedeutungsfunktion auf der Basis einer dynamischen Objektstruktur voraus und (ii) im Kontext der dynamischen Objektstruktur stellt sich die Frage, wie es möglich ist, ‚zweifelsfrei‘ von zwei vorgegebenen Beziehungen in den Prämissen auf eine dritte Beziehung als Folgerung zu ’schließen‘.

15. Diese Frage hat mindestens zwei Aspekte: (i) einmal, ob und inwieweit wir ‚im Rahmen unseres Bewusstseins‘ Kriterien finden können, die solch eine Unterscheidung unterstützen und (ii) wie die ‚Maschinerie unseres Denkens‘, die dem bewussten Denken vorgelagert ist, diese Aufgabe lösen kann. Dabei fragen wir nicht ‚empirisch‘, ’nicht naturwissenschaftlich‘, sondern ‚logisch, ‚philosophisch‘ in dem Sinne, ob wir überhaupt eine rationale Konstruktion (ein formales Modell) finden können, das eine Erklärung liefern könnte. Dass es dazu dann möglicherweise noch eine empirische Struktur geben könnte, die die Aufgabe ‚anders‘ löst, wäre interessant, würde aber in diesem Kontext dann keine Veränderung bewirken.

16. Es wird notwendig sein, alle 3x 16 Fälle einzeln anzuschauen und zu überprüfen.

17. Darüber hinaus kann man die Frage stellen, ob man die Betrachtung auf andere ‚Typen von wahrheitsfähigen Sachverhalten‘ (auf andere Typen von analytisch wahren Sachverhalten) noch ausweiten kann. Denn die Beispiele mit den Syllogismen der Figuren 1-3(4) sind sehr eng. Und da wir von der modernen formalen Logik wissen, dass man mit den modernen Kalkülen beliebig komplexe Strukturen beschreiben kann, ist die Frage nach weiteren Sachverhalten eigentlich nur eine ‚rhetorische‘ Frage. Allerdings würden wir damit in Richtung einer allgemeinen Logiktheorie steuern. Möglicherweise ist dies hier noch zu früh.

Fortsetzung folgt

QUELLEN

  • Avicenna, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
  • Digital Averroes Research Environment
  • Immanuel Kant, Critik der reinen Vernunft‘, Riga, 1781
  • Konrad Lorenz, 1973, ‚Die Rückseite des Spiegels. Versuch einer Naturgeschichte des menschlichen Erkennens‘, München, Zürich: Piper
  • Günther Patzig, ‚Die Aristotelische Syllogistik‘, 3. verb.Aufl., Göttingen: Vandenhoeck & Rupprecht, 1969
  • Nicholas Rescher (1928 – ),The Development of Arabic Logic. University of Pittsburgh Press, 1964
  • Hans-Jörg Sandkühler (Hg.) unter Mitwirkung von Dagmar Borchers, Arnim Regenbogen, Volker Schürmann und Pirmin Stekeler-Weithofer, ‚Enzyklopädie Philosophie‘, 3 Bd., Hamburg: FELIX MEINER VERLAG, 2010 (mit CD-ROM)
  • Stanford Encyclopedia of Philosophy, Aristotle’s Logic
  • Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7

Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER

AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 18

Avicenna, Logik, Logik - Alltag, Logik - Antike, Logik - formale, Prädikat, Prämisse, Subjekt, Subjekt - logisches, Syllogismus, Syloogismus - Konjunktiver, Term

(Letzte Änderung 25.Sept.2014, 09:20h)

Die ‚innere Seele‘ der Formen korrespondiert immer mit Klängen. Hier ein weiteres Klangexperiment…… der Klangraum ist unendlich groß …

VORGESCHICHTE

Für einen Überblick zu allen vorausgehenden Beiträgen dieser rekonstruierenden Lektüre von Avicennas Beitrag zur Logik siehe AVICENNAS ABHANDLUNG ZUR LOGIK – BLITZÜBERSICHT.

Avicennas Übersicht zu Wissen und syllogistischem Denken
Avicennas Übersicht zu Wissen und syllogistischem Denken

1. Nach den vorausgehenden Detailbetrachtungen weitet sich nun der Blick Avicennas auf das Wissen allgemein, und konzentriert sich im Wissen auf das schlussfolgernde Denken in Form von ‚beweisenden Syllogismen‘ (engl.: ‚demonstrative syllogisms‘). Laut Anmerkung des Übersetzers folgt er hier – wie auch in den meisten Teilen zuvor – weitgehend Aristoteles.

2. Avicenna definiert einen (beweisenden) Syllogismus durch die Komponenten (i) Jene Aussagen A1, …, An, die zum Zeitpunkt des Argumentierens als ‚wahr‘ angenommen werden, (ii) Folgerungsregeln, mittels deren man von gegebenen wahren Aussagen auf andere wahre Aussagen ‚mit Notwendigkeit folgern‘ kann, sowie (iii) jene Aussagen F1, …, Fk, die mittels solcher Folgerungsregeln aus den gemachten ‚Annahmen‘ ‚mit Notwendigkeit‘ gefolgert worden sind.

3. [Anmerkung: in einer modernen Schreibweise könnte man einen Syllogismus auch hinschreiben als $latex \{A1, …, An\} \vdash \{F1, …, Fk \}$ gelesen: die Aussagen F1, …, Fk folgen aus den Annahmen A1, …, An mit Hilfe des Folgerungsbegriffs $latex \vdash$ mit Notwendigkeit.]

4. Er unterscheidet dann zwei Arten von Syllogismen: (i) ‚Konjunktive‘ Syllogismen und (ii) ‚Disjunktive‘.

Avicenna - Konjunktiver Syllogismus - Bestandteile
Avicenna – Konjunktiver Syllogismus – Bestandteile

5. Mit der Vorstellung des ‚Konjunktiven Syllogismus‘ führt Avicenna dann – auch hier Aristoteles folgend – eine Reihe von technischen Begriffen ein, um ‚über‘ Syllogismen sprechen zu können.

6. (Konjuktive) Syllogismen bestehen aus drei ‚Aussagen‘, von denen die ersten beiden die ‚Annahmen‘ (‚Prämissen‘) sind, und die dritte die ‚Folgerung‘ (‚Konsequenz‘) aus den vorausgehenden Annahmen.

7. Annahmen wie Folgerungen bestehen jeweils aus drei ‚Ausdrucksteilen‘ A = (A1 A2 A3), von denen er die Ausdrucksteile ‚A2‘ und ‚A3‘ ‚Terme‘ nennt. Der Ausdrucksteil ‚A1‘, bekommt keine eigene Benennung, repräsentiert aber den ‚Quantor‘. Terme können ‚Subjekte S‘ oder ‚Prädikate P‘ sein.

8. Diejenigen Terme in den beiden Annahmen, die in beiden Annahmen gemeinsam sind, nennt er ‚Mittlere Terme‘. Entsprechend nennen wir die beiden anderen, komplementären, Terme hier ‚äußere Terme‘. Den Term in in einer Folgerung, der das Subjekt S repräsentiert und der kein mittlerer Term in einer Annahme ist, nennt er ‚Haupt-Term‘ (‚Major‘). Entsprechend nennt er den Term in einer Folgerung, der das Prädikat P repräsentiert und der kein mittlerer Term ist, den ‚kleinen Term‘ (‚Minor‘). Diejenige Annahme, in der der Haupt-Term der Folgerung vorkommt, wird ‚Neben-Annahme‘ genannt; die andere entsprechend ‚Haupt-Annahme‘.

9. Die typische Aussagestruktur in den Annahmen und in der Folgerung sieht dann so aus: Q (S P). Dabei ist zu beachten, dass Avicenna bei den Syllogismen keine Zeit- und keine Raum-Quantoren benutzt, sondern nur Anzahl-Quantoren, und diese treten nur ‚einfach‘ auf, indem sich der eine Quantor ‚Q‘ in Q(S P) auf die Elemente des Subjekt-Terms S bezieht. Ferner versteht er unter einer ’negativen‘ Aussage nicht die Verneinung der ganzen Aussage – also nicht $latex \neg Q(S\ P)$ –, sondern die Verneinung des Prädikat-Terms P – also $latex Q(S\ \neg P)$ –.

Avicenna Grundstrukturen der drei syllogistischen Schlussfiguren des konjunktiven Syllogismus
Avicenna Grundstrukturen der drei syllogistischen Schlussfiguren des konjunktiven Syllogismus

10. Avicenna stellt dann 3 Muster von Syllogismen vor (siehe Schaubild). Sie sind im wesentlich ’sortiert‘ nach der Verteilung der mittleren bzw. äußeren Terme. Zusätzlich zu den Mustern der mittleren Terme unterscheidet er noch, welche Quantoren die Aussagen haben und ob sie ‚affirmativ‘ oder ’negativ‘ sind.

Tabelle der Quantorenkombinationen relativ zu den Schlußfiguren
Tabelle der Quantorenkombinationen relativ zu den Schlußfiguren

11. Die Tabelle zeigt, welche Quantorenkombinationen Avicenna insgesamt berücksichtigt hat, wie er diese auf die einzelnen Schlußfiguren aufgeteilt hat, und wie ‚asymmetrisch‘ die Verteilung auf die einzelnen Schlußfiguren ausfiel. Auffällig ist, dass Avicenna nicht alle Quantorenkombinationen brücksichtigt, die möglich wären.

Avicennas Schlußfiguren und ein Beispiel für die Quantoren A, A-, E-
Avicennas Schlußfiguren und ein Beispiel für die Quantoren A, A-, E-

12. Am Beispiel der Quantorenkombination (A, A-)E- zeigt das vorausgehende Schaubild, wie unterschiedlich diese Kombination entsprechend den drei Figuren interpretiert wird. Auffällig ist, dass zwei der möglichen Kombinationen für die Schlussfiguren 1 und 2 von Avicenna nicht genutzt werden.

Fortsetzung folgt

QUELLEN

  • Avicenna, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
  • Digital Averroes Research Environment
  • Immanuel Kant, Critik der reinen Vernunft‘, Riga, 1781
  • Konrad Lorenz, 1973, ‚Die Rückseite des Spiegels. Versuch einer Naturgeschichte des menschlichen Erkennens‘, München, Zürich: Piper
  • Nicholas Rescher (1928 – ),The Development of Arabic Logic. University of Pittsburgh Press, 1964
  • Hans-Jörg Sandkühler (Hg.) unter Mitwirkung von Dagmar Borchers, Arnim Regenbogen, Volker Schürmann und Pirmin Stekeler-Weithofer, ‚Enzyklopädie Philosophie‘, 3 Bd., Hamburg: FELIX MEINER VERLAG, 2010 (mit CD-ROM)
  • Stanford Encyclopedia of Philosophy, Aristotle’s Logic
  • Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7

Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER

AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 15

Analytisch, Art (Spezies), Ausdruck - sprachlicher, Ausdruck - zusammengesetzter, Aussage, Aussagetypen, Außenraum zum Körper, Außenwelt, Avicenna, Bedeutung, Bedeutung - abstraktes Konstrukt, Bedeutung - akzidentell, Bedeutung - empirisch, Bedeutung - wesentliche, Bedeutung eines Wortes, Bedeutungsbeziehung, Bedeutungsraum, Definition, Definition - explitite, Definitorisch, Eigenschaft, Externe Welt, Falsch, Gattung (genus), Kategorien, Kognition, Logik, Logik - Alltag, Logik - Antike, Logik - formale, Logische Operatoren, Objekt, Objekt - als Eigenschaft, Objekt - echtes, Objekt - kontingent, Objekt - universell, Objekthierarchie, Objekttyp, Ontologie, ontologisch, Operator, Operator - aussagenlogischer, Prädikat, Proposition, Sein, Semantik, Subjekt, Subjekt - logisches, Wahr, Wahrheit, Wahrheit - definitorische (analytische), Wahrheit - ontologische, Wahrheit als Übereinstimmung, Wahrheitsbegriff, wahrheitsfähig, Wahrheitsgehalt, Wahrheitskriterium, Wahrheitswert

VORGESCHICHTE

Für einen Überblick zu allen vorausgehenden Beiträgen dieser rekonstruierenden Lektüre von Avicennas Beitrag zur Logik siehe AVICENNAS ABHANDLUNG ZUR LOGIK – BLITZÜBERSICHT.

Übersicht zum Wissen K bestehend aus Ausdrücken E, Objekten O sowie Bedeutungsbeziehungen M
Übersicht zum Wissen K bestehend aus Ausdrücken E, Objekten O sowie Bedeutungsbeziehungen M

WAHR UND FALSCHE AUSSAGEN

1. Nach dem Blogeintrag Avicenna 14b gibt es jetzt Ausdrücke A, B, …, die ‚wahr‘ oder ‚falsch‘ sein können und die wir deshalb ‚Aussagen‘ (auch ‚Propositionen‘) nennen. Aussagen können mittels aussagenlogischer Operatoren wie ‚NEGATION‘, ‚UND‘, ‚IMPLIKATION‘ usw. zu komplexeren Ausdrücken so verknüpft werden, dass jederzeit ermittelt werden kann, wie der Wahrheitswert des komplexen Ausdrucks lautet, wenn die Wahrheitswerte der Teilausdrücke bekannt sind. Ob im Einzelfall eine Aussage A ‚wahr‘ oder ‚falsch‘ ist, muss durch Rückgriff auf ihre Bedeutungsbeziehung M(A) geklärt werden. Bislang ist nur klar, dass die Bedeutungsbeziehung M nur allgemein eine Beziehung zu den (kognitiven) Objekten O herstellt (siehe Grafik oben).

2. Avicenna spricht aber nicht nur von Aussagen A allgemein, sondern unterscheidet die Teilausdrücke ‚Subjekt‘ S und ‚Prädikat‘ P, zusätzlich oft noch ‚Quantoren‘ Q.

FEINSTRUKTUR DER BEDEUTUNG VON AUSDRÜCKEN

3. Man kann und muss dann die Frage stellen, ob und wie sich auf der Bedeutungsseite die Unterscheidung in S und P auf der Ausdrucksseite widerspiegelt?

ECHTE UND UNECHTE OBJEKTE

4. In vorausgehenden Blogeinträgen zu Avicenna (Avicenna 4, 5, 7 und 11) wurde schon unterschieden zwischen ‚echten‘ und ‚unechten‘ Objekten. ‚Unechte Objekte‘ sind solche Wissenstatbestände, die man zwar identifizieren und unterscheiden kann, die aber immer nur im Kontext von ‚echten Objekten‘ auftreten. ‚Unechte‘ Objekte werden meistens als ‚Eigenschaften‘ bezeichnet. Beispiel: die Farbe ‚Rot‘ können wir wahrnehmen und z.B. von der Farbe ‚Blau‘ unterscheiden, die Farbe ‚Rot‘ tritt aber nie alleine auf so wie z.B. Gegenstände (Tassen, Stühle, Früchte, Blumen, …) alleine auftreten.

5. Hier wird davon ausgegangen, dass die Objekthierarchie O primär von echten Objekten gebildet wird; unechte Objekte als Eigenschaften treten nur im Kontext eines echten Objekts auf.

GATTUNG UND ART; KATEGORIEN

6. Ein Objekt kann viele Eigenschaften umfassen. Wenn es mehr als ein Objekt gibt – also O1, O2, … — die sowohl Eigenschaften Ex gemeinsam haben wie auch Eigenschaften Ey, die unterschiedlich sind, dann kann man sagen, dass alle Objekte, die die Eigenschaften Ex gemeinsam haben, eine ‚Gattung‘ (‚genus‘) bilden, und dass man anhand der ‚unterscheidenden Eigenschaften Ey‘ unterschiedliche ‚Arten‘ (’species‘) innerhalb der Gattung unterscheiden kann.

7. Gattungen, die keine Gattungen mehr ‚über sich‘ haben können, sollen hier ‚Kategorien‘ genannt werden.

ONTOLOGISCHE UND DEFINITORISCHE (ANALYTISCHE) WAHRHEIT

8. Bislang ist der Wahrheitsbegriff $latex \top, \bot$ in dieser Diskussion an der hinreichenden Ähnlichkeit eines vorgestellten/ gedachten kognitiven) Objekts $latex a \in Oa$ mit sinnlichen wahrnehmbaren Eigenschaften $latex s \subseteq Os$ festgemacht worden. Ein ‚rein gedachtes Objekt $latex a \in Oa$ ist in diesem Sinne weder ‚wahr‘ $latex \top$ noch ‚falsch‘ $latex \bot$.

9. Setzt man allerdings eine Objekthierarchie O voraus, in der man von einem beliebigen individuellem Objekt a immer sagen kann, zu welchem Objekt Y es als seiner Gattung gehört, dann kann man eine Aussagen der Art bilden ‚a ist eine Tasse‘.

10. Wenn man zuvor in einer Definition vereinbart haben sollte, dass zum Begriff der ‚Tasse‘ wesentlich die Eigenschaften Ex gehören, und das Objekt a hätte die Eigenschaften $latex Ex \cup Ey$, dann würde man sagen, dass die Aussage ‚a ist eine Tasse‘ ‚wahr‘ ist, unabhängig davon, ob es zum kognitiven Objekt a ein ’sinnliches‘ ‚Pendant‘ geben würde oder nicht. Die Aussage ‚a ist eine Tasse‘ wäre dann ‚rein definitorisch‘ (bzw. ‚rein analytisch‘) ‚wahr.

11. Im Gegensatz zu solch einer rein definitorischen (analytischen) Wahrheit eines Objekts a, die als solche nichts darüber sagt, ob es das Objekt a ‚tatsächlich‘ gibt, soll hier die ursprünglich vereinbarte ‚Wahrheit‘ durch Bezug auf eine ’sinnliche Gegebenheit‘ $latex s \subseteq Os$ ‚ontologische‘ Wahrheit genannt werden, also einer Wahrheit, die sich auf das ‚real Seiende‘ in der umgebenden Welt W bezieht.

12. [Anmerkung: Dieses – auch im Alltagsdenken – unterstellte ‚Sein‘, die unterstellte übergreifende ‚Realität‘ ist nicht nur eine ‚Extrapolation‘ aufgrund sinnlicher Gegebenheiten ‚im‘ wissenden System, sondern ist in seiner unterstellten ‚Realität‘ auch nur eine sehr spezifische Form von Realität. Wie wir heute aufgrund immer komplexerer Messprozeduren wissen, gibt es ‚Realitäten‘, die weit jenseits aller sinnlichen Qualitäten liegen. Es fällt uns nur nicht so auf, weil diese gemessenen Eigenschaften X durch allerlei Prozeduren für unsere Sinnesorgane ‚umgerechnet‘, ‚transformiert‘ werden, so dass wir etwas ‚Sehen‘ oder ‚Hören‘, obgleich das gemessene X nicht zu sehen oder zu hören ist.]

13. Solange wir uns in unseren Aussagen auf das Enthaltensein eines Objektes a in einem Gattungsobjekts X beschränken ‚a ist ein X‘ oder das Feststellen von Eigenschaften der Art ‚a hat b‘ kann man sagen, dass eine Aussagestruktur wie (S P) wie folgt interpretiert werden kann: Es gibt einen Ausdruck A=(AsAp), bei dem ein Ausdrucksteil As sich auf ein echtes Objekt M(As) = $latex a \in Oa$ bezieht und der andere Ausdrucksteil Ap bezieht sich auf die Beziehung zwischen dem Objekt a und entweder einem Gattungsobjekt X (Ap = ‚ist ein X‘) oder auf eine Eigenschaft Y (Ap = ‚hat Y‘).

14. Derjenige Ausdrucksteil As, der sich auf das echte Objekt a bezieht, ‚von dem‘ etwas ausgesagt werden soll (‚ist ein…‘, ‚hat …‘), dieser Ausdrucksteil wird als ‚Subjekt‘ S bezeichnet, und der Ausdrucksteil Ap, mittels dem etwas über das Subjekt ausgesagt wird, wird ‚Prädikat‘ P genannt.

15. Hierbei ist eine gewisse ‚Asymmetrie‘ zu beachten. Die Bedeutung vom Ausdrucksteil As – M(As) – bezieht sich auf eine ‚konkrete‘ Eigenschaftsstruktur innerhalb der Objekthierarchie. Die Bedeutung vom Ausdrucksteil Ap – M(Ap) – bezieht sich auf eine ‚Beziehung‘ / ‚Relation’/ ein ‚Verhältnis‘ [R] zwischen dem bezeichneten Bedeutungsobjekt M(As) = a und einem anderen bezeichneten Bedeutungsobjekt M(Ap), also R(M(As), M(Ap)). Die Beziehung R ist selbst kein ‚Objekt‘ so wie das Objekt a oder das implizit angenommene ‚Bezugsobjekt‘ X bzw. Y von a. Eine solche Beziehung R setzt – um prozessural ‚hantierbar‘ zu sein – eine zusätzliche ‚Objektebene‘ voraus, auf der es ein R-Objekt gibt, das die Beziehung zwischen dem a-Objekt und dem X-Y-Objekt ‚repräsentiert.

16. [Anmerkung: Bei ’neuronalen Netzen‘ wäre das R-Objekt jenes Neuron, das die Verbindung zwischen zwei anderen Neuronen ‚realisiert‘.]

17. Fassen wir zusammen: Bei einem Ausdruck A der Art A=’Hans ist ein Mensch‘ gibt es den Ausdrucksteil As=’Hans‘ und den Ausdrucksteil Ap=’ist ein Mensch‘. Die Bedeutung des Ausdrucksteils As M(As) als M(‚Hans‘) ist ein Objekt h in der unterstellten Bedeutungshierarchie O des Sprechers, das gewisse Eigenschaften E(h) besitzt. Die Bedeutung des Ausdrucksteils Ap als M(Ap) bzw. M(‚ist ein Mensch‘) ist sowohl ein Objekt M mit Eigenschaften E(M) als auch eine Beziehung R_ist zwischen dem Objekt h und dem Objekt M, also R_ist(h,M). Die Beziehung ist definitorisch/ analytisch ‚wahr‘ wenn es gilt, dass die definierenden Eigenschaften E(M) des Objekts Mensch M auch bei den Eigenschaften E(h) von Hans zu finden sind, also $latex E(M) \subset E(h)$ .

BEZIEHUNGSRAUM – TRANSZENDENTALE BEDINGUNGEN

18.

Fortsetzung folgt

QUELLEN

  • Avicenna, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
  • Digital Averroes Research Environment
  • Nicholas Rescher (1928 – ),The Development of Arabic Logic. University of Pittsburgh Press, 1964
  • Hans-Jörg Sandkühler (Hg.) unter Mitwirkung von Dagmar Borchers, Arnim Regenbogen, Volker Schürmann und Pirmin Stekeler-Weithofer, ‚Enzyklopädie Philosophie‘, 3 Bd., Hamburg: FELIX MEINER VERLAG, 2010 (mit CD-ROM)
  • Stanford Encyclopedia of Philosophy, Aristotle’s Logic
  • Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7

Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER

AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 14

Aussage, Aussagetypen, Außenraum zum Körper, Außenwelt, Avicenna, Bedeutung, Bedeutung - abstraktes Konstrukt, Bedeutung - empirisch, Bedeutung eines Wortes, Bedeutungsbeziehung, Bedeutungskorrelat, Bedeutungsmaterial, Bedeutungsraum, Erfüllung, Falsch, Logik, Logik - Alltag, Logik - Antike, Logische Operatoren, Möglichkeit, Notwendig, Operator, Operator - aussagenlogischer, Semantik, Wahr, Wahrheit, Wissen, Wissen - gefolgertes, Wissen - sensorisches, Wissen - sprachlich vermitteltes, Zutreffen

VORGESCHICHTE

Für einen Überblick zu allen vorausgehenden Beiträgen dieser rekonstruierenden Lektüre von Avicennas Beitrag zur Logik siehe AVICENNAS ABHANDLUNG ZUR LOGIK – BLITZÜBERSICHT.

1. Wenn also eine Formulierung von Konvertierungsregeln nicht ohne Bezug auf irgend eine Bedeutung M hinter den Ausdrücken möglich ist, stellt sich zum wiederholten Male die Frage, über welche mögliche Bedeutung M ‚hinter‘ den Ausdrücken gesprochen werden muss.

KONVERTIERUNG MIT BEDEUTUNG – MIT WELCHER?

2. Beginnen wir mit dem Ausgangspunkt, dass Aussagen PROP solche Ausdrücke von der Menge aller Ausdrücke E sind, die ‚wahr‘ oder ‚falsch‘ sein können. ‚Treffen sie zu‘ gelten sie als ‚wahr‘; ‚treffen sie nicht zu‘ gelten sie als ‚falsch‘.
3. Bislang hatten wir schon die generelle Annahme geäußert, dass das Denken und Wissen eines Menschen im ‚Innern‘ dieses Menschen zu verorten sei und der Mensch ‚in‘ einer umgebenden Welt W mit realen Ereignissen X vorkommt.
4. Um die Begriffe ‚wahr/ falsch‘ bzw. ‚zutreffen/ nicht zutreffen‘ zu ‚erklären‘, nehmen wir an, dass die Menge des möglichen Wissens K eines einzelnen Menschen sich zerlegen lässt in die Teilmengen ‚Vorgestellt‘ K_v, ‚Erinnert‘ K_m sowie ’sinnlich präsent‘ K_s. Es gilt also $latex K = K_{s} \cup M_{v} \cup M_{m}$.
5. Eine Bedeutung wird dann durch eine Beziehung zwischen dem Wissen K und möglichen Ausdrücken $latex PROP \subseteq E$ gebildet: $latex M \subseteq PROP \times K$.
6. Speziell gilt aber, dass man zwischen einer ’neutralen‘ Bedeutung $latex M_n \subseteq E \times (K_{v} \cup K_{m})$ unterscheiden muss, die weder ‚wahr‘ noch ‚falsch‘ ist, und der ’sinnlich fundierten‘ Bedeutung $latex M_s \subseteq E \times K_{s}$. Gibt es zwischen einer neutralen Bedeutung $latex M_{n}$ und einer sinnlich fundierten Bedeutung $latex M_{s}$ eine Beziehung des ‚Zutreffens‘ $latex M_{s} \models M_{n}$, dann kann man sagen, dass das Wissen $latex K_{n}$ in dieser Beziehung ‚wahr‘ ist, andernfalls nicht, geschrieben $latex M_{s} \not\models K_{n}$.
7. Zusätzlich kann man im Bereich des erinnerten Wissens $latex K_{m}$ noch unterscheiden zwischen einem solchen, das Bezug zu ‚vormals sinnlich fundiertem Wissen‘ aufweist als $latex K_{ms}$ und solchem, das ‚keinen Bezug zu vormals fundiertem sinnlichen Wissen‘ aufweist als $latex K_{mns}$.
8. Erinnertes Wissen mit Bezug zu vormals fundiertem Wissen $latex K_{ms}$ hat die Eigenart, dass sich in Abhängigkeit von der ‚Häufigkeit‘ der erinnerbaren Wissenselementen in $latex K_{ms}$ eine Art ‚Erwartung‘ bzgl. des neuerlichen Eintretens dieses Wissens als sinnliches Wissen $latex K_{vs}$ ausbildet: $latex \mu: K_{ms} \longrightarrow K_{vs}$ mit $latex K_{vs} \subseteq K_{v}$, d.h. im Bereich des vorgestellten Wissens $latex K_{v}$ gibt es solches mit einem speziellen Erwartungsanteil $latex K_{vs}$ hervorgerufen durch besondere Erinnerungen.

EXKLUSIVE MODALOPERATOREN

9. An dieser Stelle könnte man dann noch die Begriffe ‚möglich‘ $latex \diamond$ und ’notwendig‘ $latex \boxempty$ wie folgt einführen: ein vorgestelltes Wissen gilt als ‚möglich‘, wenn der Erwartungswert nicht gleich 1 ist, also $latex \diamond K_{v} \leftrightarrow \mu(K_{v}) \not= 1$, andernfalls als notwendig, also $latex \boxempty K_{v} \leftrightarrow \mu(K_{v}) = 1$
10. Daraus kann man ableiten, dass gelten soll $latex \boxempty K_{v} \leftrightarrow \neg\diamond K_{v}$ oder $latex \neg\boxempty K_{v} \leftrightarrow \diamond K_{v}$.
11. Diese Definition von ‚möglich‘ und ’notwendig‘ entspricht nicht ganz der ‚Intuition‘, dass etwas, was ’notwendig‘ ist, auf jeden Fall auch möglich sein sollte; allerdings folgt – intuitiv — aus der Möglichkeit keine Notwendigkeit. Die vorausgehende Definition von möglich und notwendig erinnert ein wenig an das ‚exklusive Oder‘, das auch ’schärfer‘ ist als das normale Oder. Nennen wie die hier benutzte Definition von ‚möglich‘ $latex \diamond$ und ’notwendig‘ $latex \boxempty$ daher auch die ‚exklusiven Modaloperatoren‘: Wenn etwas notwendig ist, dann ist es nicht möglich, und wenn etwas möglich ist, dann ist es nicht notwendig.
12. Anmerkung: wenn etwas ‚gedanklich notwendig‘ ist, folgt daraus in diesem Rahmen allerdings nicht, dass es auch tatsächlich sinnlich eintritt. Aus der gedanklichen Notwendigkeit folgt nur, dass es in der erinnerbaren Vergangenheit bislang immer eingetreten ist und daher die Erwartung sehr hoch ist, dass es wieder eintreten wird.

WAHR und FALSCH ABKÜRZUNGEN

13. Wenn man von einer Aussage $latex e \in E$ sagen kann, dass das zugehörige vorstellbare Wissen $latex M(e)=K_{v}$ ‚wahr‘ ist, weil es auf ein sinnliches Wissen $latex K_{s}$ ‚zutrifft oder eben ‚falsch‘, weil es ’nicht zutrifft‘, dann soll dieser Sachverhalt hier wie folgt abgekürzt werden:
14. Eine Aussage A soll genau dann mit ‚wahr‘ $latex \top$ bezeichnet werden, wenn es ein sinnliches Wissen gibt, das das zugehörige vorgestellte Wissen ‚erfüllt‘, also $latex (A)\top \leftrightarrow M(A)=K_{v}$ und es gibt ein sinnlich fundiertes Wissen $latex K_{s}$, so dass gilt $latex K_{s} \models K_{v}$.
15. Eine Aussage A soll genau dann mit ‚falsch‘ $latex \bot$ bezeichnet werden, wenn es kein sinnliches Wissen gibt, das das zugehörige vorgestellte Wissen ‚erfüllt‘, also $latex (A)\bot \leftrightarrow M(A)=K_{v}$ und $latex K_{s} \not\models K_{v}$. [Anmerkung: Es gibt nur ein einziges sinnlich fundiertes Wissen, und zwar das jeweils aktuelle!]

AUSSAGEOPERATOREN

16. Jetzt kann man folgende Operatoren über Aussagen definieren:
17. NEGATION: die Verneinung einer Aussage A ist wahr, wenn die Aussage selbst falsch ist, also $latex (\neg A)\top \leftrightarrow (A)\bot$.
18. KONJUNKTION: die Konjunktion $latex \wedge$ von zwei Aussagen A und B ist wahr, wenn beide Aussagen zugleich wahr sind; ansonsten ist die Konjunktion falsch, also $latex (A \wedge B)\top \leftrightarrow (A)\top\ und\ zugleich\ (B)\top$; ansonsten falsch.
19. DISJUNKTION: die Disjunktion $latex \vee$ von zwei Aussagen A und B ist wahr, wenn eine von beiden Aussagen wahr ist; ansonsten ist die Disjunktion falsch, also $latex (A \vee B)\top \leftrightarrow (A)\top\ oder\ (B)\top$; ansonsten falsch.
20. EXKLUSIVE DISJUNKTION: die exklusive Disjunktion $latex \sqcup$ von zwei Aussagen A und B ist wahr, wenn genau eine von beiden Aussagen wahr ist; ansonsten ist die exklusive Disjunktion falsch, also $latex (A \sqcup B)\top \leftrightarrow\ Entweder\ (A)\top\ oder\ (B)\top$; ansonsten falsch.
21. IMPLIKATION: die Implikation $latex \rightarrow$ von zwei Aussagen A und B ist wahr, wenn nicht A wahr ist und zugleich B falsch, also $latex (A \rightarrow B)\top \leftrightarrow\ nicht (A)\top\ und\ zugleich\ (B)\bot$; ansonsten falsch.

Fortsetzung folgt

QUELLEN

  • Avicenna, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
  • Digital Averroes Research Environment
  • Nicholas Rescher (1928 – ),The Development of Arabic Logic. University of Pittsburgh Press, 1964
  • Stanford Encyclopedia of Philosophy, Aristotle’s Logic
  • Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7

Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER.

AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 13

Allquantor, Avicenna, Bedeutung, Bedeutung eines Wortes, Bedeutungsbeziehung, Bedeutungskorrelat, Bedeutungsmaterial, Beweis - logischer, Falsch, Folgern - logisches, Konvertierung von Ausdrucksformen, Logik, Logik - Alltag, Logik - Antike, Logik - formale, Partikularquantor, Prädikat, Quantor, Quantor - partikulär, Quantor - universell, Semantik, Subjekt, Wahr, Wahrheit

(Letzte Änderung 8.Sept.2014, 02:59h)

VORGESCHICHTE

Für einen Überblick zu allen vorausgehenden Beiträgen dieser rekonstruierenden Lektüre von Avicennas Beitrag zur Logik siehe AVICENNAS ABHANDLUNG ZUR LOGIK – BLITZÜBERSICHT.

AVICENNAS DISKUSSION VON UMWANDLUNG (‚Conversion‘)

1. Aus der englischen Übersetzung ist nicht klar zu entnehmen, ob der Begriff ‚Umwandlung‘ (engl.: ‚conversion‘) tatsächlich eine Form von ‚Umwandlung’/ ‚Umformung’/ ‚Konvertierung‘ meint oder spezieller eine Umformung von Aussagen, die letztlich eine ‚logische Folgerung‘ darstellen. Letztere Interpretation wird angeregt, da er dann tatsächlich an entscheidender Stelle zum ersten Mal in der ganzen Abhandlung eine Folge von Aussagen präsentiert, die man als ‚Folgerungstext‘ interpretieren kann.

2. In seiner Kerndefinition gleich zu Beginn charakterisiert er den Ausdruck ‚Umformung‘ mit Bezug auf zwei Ausdrücke A und B, die Subjekte, Prädikate, Antezedenz und Konsequenz enthalten können (implizit auch Quantoren, da er diese im folgenden Text beständig benutzt). Jede der beiden Aussagen hat eine Bedeutung M(A) bzw. M(B). Umformung hat jetzt damit zu tun, dass einzelne dieser logischen Rollen (Q, S, P, …) ‚ausgetauscht‘ werden, ohne dass dadurch die ‚Bedeutung‘ verändert wird.

3. [Anmerkung: Hier gibt es folgende Unklarheiten: (i) Sollen die Bedeutungen M(A) und M(B) von vornherein ‚gleich‘ sein, und zwar so, dass sie nach dem Austausch unverändert sind? oder (ii) sind die Bedeutungen M(A) und M(B) von vornherein ungleich, sollen aber, jede für sich, auch nach der Umformung gleich sein? In beiden Fällen – so interpretiere ich seine Aussage von Avicenna, gibt es eine Bedeutung vor der Umformung – eine gemeinsame oder eine individuelle –, die nach der Umformung ‚gleich‘ geblieben ist. Schreiben wir für die Umformung als $latex \vdash$, dann würde bedeuten ‚$latex A \vdash B$‘ A wird nach B umgeformt, so dass die Bedeutung von A und B – gemeinsam oder individuell – erhalten bleibt. Es stellt sich hier wieder das Problem – wie im gesamten vorausgehenden Text –, dass der Begriff ‚Bedeutung‘ bei Avicenna nicht scharf definiert ist. Er kann alles und nichts bedeuten. Die ‚Gleichheit‘ von zwei Bedeutungen M_vorher und M_nachher ist also ein ‚offener Begriff‘.]

4. In dem folgenden Text präsentiert Avicenna einerseits einige Beispiele von Umformungen ohne genauere Begründungen, in einem Fall präsentiert er aber das Beispiel einer ausführlicheren Begründung, die wie eine Folgerungstext (wie ein logischer Beweis) aussieht. Beginnen wir mit den Beispielen ohne Begründung.

5. Mögliche Konversion: Von ‚Kein Mensch ist unsterblich‘ ($latex \neg\exists (Mensch)(ist)(unsterblich)$) kann man bedeutungserhaltend umformen in ‚Kein Unsterblicher ist ein Mensch‘ ($latex (\neg\exists (Unsterblicher)(ist)(Mensch)$).

6. Avicenna stellt die Regel auf: Von einer affirmativen All-Aussage kann ich nicht zu einer anderen affirmativen All-Aussage konvertieren.

7. Beispiel: Von ‚Jeder Mensch ist ein Lebewesen‘ kann ich nicht umformen zu ‚Jedes Lebewesen ist ein Mensch‘ (mehr formalisiert: ($latex \forall (Mensch)(ist)(Lebwesen)$) kann nicht umgeformt werden zu ($latex \forall (Lebewesen)(ist)(Mensch)$).

8. Avicenna stellt die Regel auf: Die Umformung einer affirmativen All-Aussage ist eine affirmative Partikular-Aussage.

9. Beispiel: Die Aussage ‚Alle F sind B‘ kann umgeformt werden zu ‚Einige B sind F‘ (Formalisierter: Den Ausdruck $latex \forall (F)(sind)(B)$) kann man umformen zu ($latex \exists(B)(ist)(F)$))

10. Avicenna stellt die Regel auf: Eine affirmative Partikular-Aussage kann umgeformt werden in eine affirmative Partikular-Aussage.

11. Beispiel: Der Ausdruck ‚Einige F sind B‘ kann umgeformt werden zu ‚Einige B sind F‘ (Formalisierter: ($latex \exists (F)(sind)(B)$) $latex \vdash$ ($latex \exists (B)(sind)(F)$)).

12. Avicenna stellt die Regel auf: Eine negative Partikular-Aussage kann nicht konvertiert werden.

13. Beispiel: Die Aussage ‚Kein Lebewesen ist ein Mensch‘ kann nicht konvertiert werden zu ‚Kein Mensch ist ein Lebewesen‘. (mehr formalisiert: ($latex \neg\exists (Lebewesen)(ist)(Mensch)$) $latex \not\vdash$ ($latex \neg\exists (Mensch)(ist)(Lebewesen)$))

14. [Anmerkung: Hier gibt es einigen Diskussionsbedarf. Bevor die Diskussion eröffnet wird, hier aber noch das Konvertierungsbeispiel, das wie ein Folgerungstext aussieht.]

15. Ausgangspunkt ist die Regel: Eine negative All-Aussage kann in eine negative All-Aussage konvertiert werden mit dem Beispiel: Von ($latex \neg\exists (Mensch)(ist)(Unsterblicher)$) $latex \vdash$ ($latex \neg\exists (Unsterblicher)(ist)(Mensch)$).

16. Avicenna nennt die nun folgende ‚Folge von Aussagen‘ explizit einen ‚Beweis‘ (engl.: ‚proof‘).

17. Wenn es ‚wahr‘ ist, dass gilt (Kein F ist B), dann ist es auch wahr, dass (Kein B ist F). Andernfalls [wäre der Wenn-Dann-Zusammenhang nicht wahr] würde der Widerspruch (engl.: ‚contradictory‘) folgen (Einige B sind F).

18. [Anmerkung: Zur Erinnerung, die Negation einer Implikation (Wenn A dann B) ist nur wahr, wenn A wahr wäre und zugleich B falsch, also ’nicht B‘, d.h. ’nicht(Kein B ist F)‘ d.h. (einige B sind F). Insofern bildet die Aussage (Einige B sind F) einen logischen Widerspruch zu (Kein B ist F). ]

19. Der Beweis beginnt damit, dass Avicenna eine Abkürzung einführt: Er definiert ‚H := ‚Einige B‘. [ein sehr gefährliches Unterfangen…]

20. Dann folgert er ‚H ist gleichbedeutend mit F‘

21. Er folgert weiter: ‚H ist sowohl F als auch B [Damit unterschlägt er, dass H eigentlich nur ‚einige‘ B meinen sollte]

22. Er folgert weiter: Dann gibt es ein F, das auch B ist ($latex \exists (F)(ist)(B)$

23. Er folgert weiter: Nehme ich die Aussage (Einige B sind F) als wahr an, dann komme ich zu der Aussage (Einige F sind B); dies steht aber im Widerspruch zu der Ausgangsbehauptung, das ‚Kein F ist B‘.

24. Er folgert weiter: Deshalb ist es nicht möglich, von der Ausgangsbehauptung ‚Wenn es ‚wahr‘ ist, dass gilt (Kein F ist B), dann ist es auch wahr, dass (Kein B ist F)‘ auf den Widerspruch ‚Einige F sind B‘ zu schließen.

25. Avicenna folgert weiter: Von daher, wenn es gilt, dass ‚Kein F ist B‘, dann gilt auch die Konvertierung ‚Kein B ist F‘.

DISKUSSION

KONVERTIERBARKEIT DER FORMEN (Q (A B)) zu (Q (B A)) – BEDEUTUNGSABHÄNGIG

26. In den Beispielen, die Avicenna präsentiert, gibt es zwei Beispiele, die verwirrend sind. Im einen Fall will er über ’negative All-Aussagen‘ ($latex \neg\forall$) sprechen und im anderen Fall über ’negative Partikular-Aussagen‘ ($latex \neg\exists$). Das Beispiel für negative All-Aussagen lautet ‚Kein Mensch ist unsterblich‘. Der Quantor ‚kein‘ ist aber definiert als ’nicht einige‘ bzw. ‚$latex \neg\exists$‘. Dies aber ist gleichbedeutend mit einer negativen Partikular-Aussage. Später präsentiert er als Beispiel für negative Partikular-Aussagen den Ausdruck ‚Kein Lebewesen ist ein Mensch‘ ($latex \neg\exists (Lebewesen)(ist)(Mensch)$).

27. Damit haben wir es mit folgenden Widersprüchlichkeiten zu tun: (i) Avicenna interpretiert seinen Begriff der negativen Allaussagen mit einem Beispiel, das eine negative Partikular-Aussage repräsentiert; (ii) Mit einem Beispiel, das eine negative Partikular-Aussage repräsentiert, argumentiert er, dass man bedeutungserhaltend negative All-Aussagen konvertieren kann; (iii) Mit einem anderen Beispiel einer negativen Partikularaussage argumentiert er, man könne dieses nicht konvertieren.

28. Da das Beispiel zu (ii) zeigt, dass man sehr wohl eine negative Partikular-Aussage konvertieren kann, fragt man sich, warum es in einem anderen Fall nicht gehen soll. Dazu kommt, dass das konkrete Beispiel, das Avicenna präsentiert, aus sich heraus fragwürdig erscheint: ‚Kein Lebewesen ist ein Mensch‘ soll nicht konvertierbar sein zu ‚Kein Mensch ist ein Lebewesen‘. (mehr formalisiert: ($latex \neg\exists (Lebewesen)(ist)(Mensch)$) $latex \not\vdash$ ($latex \neg\exists (Mensch)(ist)(Lebewesen)$))

29. Bekannt ist – zumindest bezogen auf diese Begriffe –, dass sehr wohl einige Lebewesen Menschen sind, also eher gilt $latex \neg\neg\exists (Lebewesen)(ist)(Mensch)$, d.h. $latex \exists (Lebewesen)(ist)(Mensch)$. Von einer Aussage wie $latex \neg\exists (Mensch)(ist)\neg(Lebewesen)$) könnte man allerdings nicht konvertieren zu $latex \neg\exists (Lebewesen)(ist)\neg(Mensch)$).

30. Trotzdem gibt es eine mögliche Konvertierung von ($latex \neg\exists (Mensch)(ist)(Unsterblich)$)) zu ($latex \neg\exists (Unsterblich)(ist)(Mensch)$)).

31. Diese Beispiele legen die Vermutung nahe, dass die bisherigen ‚Konvertierungsregeln‘ von Avicenna nicht unabhängig sind von der jeweils unterstellten Bedeutung der beteiligten Subjekte und Prädikate.

32. Bezogen auf die Struktur (Q (A B)) $latex \vdash (Q (B A))$ hängt die Möglichkeit oder Unmöglichkeit einer Konvertierung in den Beispielen davon ab, wie sich die Bedeutungen von A und B, also M(A) und M(B), zueinander verhalten.

33. Zwei Hauptfälle kann man unterscheiden: (i) die Bedeutung von beiden Ausdrücken ist ‚gleich‘, d.h. M(A) = M(B), oder (ii) die Bedeutungen sind ungleich in dem Sinne, dass zwar alle Elemente, die zu M(B) gehören auch in M(A) sind, aber nicht umgekehrt, also $latex M(B) \subseteq M(A)$.

34. Wenn wir Fall (i) M(A) = M(B) unterstellen können, dann kann man von $latex \forall A sind B$ auf $latex \forall B sind A$ schließen, oder $latex \exists A sind B$ und umgekehrt. Die Aussage $latex \neg\forall A sind B$ wäre formal zwar möglich, wäre aber ’semantisch‘ (aufgrund der angenommenen Bedeutung) aber nicht möglich. Genau sowenig wie $latex \neg\exists A sind B$ semantisch möglich wäre, wohl aber syntaktisch.

35. Unterstellen wir hingegen den Fall (ii) $latex M(B) \subseteq M(A)$, dann würde die Konvertierung von $latex \forall A sind B$ auf $latex \forall B sind A$ nicht gelten. Entsprechend kann man die wahre Aussage $latex \forall B sind A$ nicht konvertieren zu $latex \forall A sind B$. Die Konvertierung $latex \exists A sind B$ würde gehen wie auch umgekehrt. Die Aussage $latex \neg\forall A sind B$ ist wahr, die Konvertierung zu $latex \neg\forall B sind A$ wäre falsch. Usw.

36. Diese Beispiele verdeutlichen, dass die Konvertierbarkeit von Ausdrücken der Form (Q (A B)) zu (Q (B A)) eindeutig von der angenommenen Bedeutungsstruktur abhängig ist (zumindest in dem Kontext, den Avicenna diskutiert). Betrachten wir seine anderen Konvertierungsregeln.

37. (i) Von einer affirmativen All-Aussage kann ich nicht zu einer anderen affirmativen All-Aussage konvertieren.

38. (ii) Die Umformung einer affirmativen All-Aussage ist eine affirmative Partikular-Aussage.

39. (iii) Eine affirmative Partikular-Aussage kann umgeformt werden in eine affirmative Partikular-Aussage.

40. (iv) Eine negative Partikular-Aussage kann nicht konvertiert werden.

41. Zu (i): Nehmen wir an, dass gilt ($latex M(A) = M(B)$), dann trifft diese Regel zu. Nehmen wir aber an, dass gilt ($latex M(B) \subseteq M(A)$), dann gilt diese Regel nicht.

42. Zu (ii) und (iii): Nehmen wir an, dass gilt ($latex M(A) = M(B)$), dann trifft diese Regel zu. Nehmen wir aber an, dass gilt ($latex M(B) \subseteq M(A)$), dann gilt diese Regel auch.

43. Zu (iv): Dieser Fall ist von der Form her (rein syntaktisch) möglich, von der Bedeutung her (rein semantisch) aber ausgeschlossen.

44. Bei allen bisherigen Konvertierungsbeispiele von Avicenna ist zu beachten, dass sich die Bedeutung des Subjekts S und des Prädikats P in einer Aussage (S P) in der Art $latex M(A) = M(B)$ oder $latex M(B) \subseteq M(A)$ beschreiben lässt. Dies setzt voraus, dass sich ein Prädikat P auch als eine Menge von Objekten auffassen lässt, denen eine bestimmte Eigenschaft E zukommt, also etwa P := ‚eine Menge von Elementen, die die Eigenschaft P haben‘. Zu sagen ‚S ist P‘ würde dann sagen, dass die Elemente die S sind auch die Elemente sind, die P sind.

45. Man muss hier die Frage stellen, ob Prädikate immer diese Form haben.

KONVERTIERUNG OHNE BEDEUTUNG?

46. Macht man die Konvertierbarkeit von Ausdrücken der Form (Q (A B)) und (Q (B A)) von der Bedeutung M der Ausdrücke A und B abhängig, dann hängt die Formulierung der Konvertierungsregeln ab von einer brauchbaren Definition des zugrundeliegenden Bedeutungsraumes samt seiner Interaktion mit den Ausdrucksformen. Im weiteren Verlauf soll dies explizit untersucht werden. Es stellt sich aber auch die Frage, ob man Konvertierungsregeln nicht auch ohne Rückgriff auf die Bedeutung der Teilausdrücke formulieren kann.

47. Hat man nur die Ausdrücke (Q (S P)) mit der Verallgemeinerung, dass S und P ‚gleichwertig‘ sein können im Sinne von (Q (A B)) $latex \vdash$ (Q (B A)), dann stellt sich die Frage welche Kriterien man hätte, gäbe es keinen Bedeutungsbezug?

48. Man muss feststellen, dass ohne irgendeinen Bedeutungsbezug die Ausdrücke als solche keinerlei Ansatzpunkt bieten, eine Konvertierung zuzulassen oder sie zu verbieten.

49. Wenn aber Konvertierungsregeln ohne Bedeutung keinen Sinn machen, dann muss man sich fragen, welche Bedeutungsstrukturen man benötigt, dass man solche Konvertierungsregeln sinnvoll einführen kann.

KONVERTIERUNG MIT BEDEUTUNG – MIT WELCHER?

50. Wenn es also ohne Bezug auf eine Bedeutung nicht geht, stellt sich die Frage, wie eine solche Bedeutungsstruktur aussehen muss, damit solche – oder auch andere – Konvertierungsregeln formuliert werden können.

51. Die weitere Diskussion wird in einem neuen Blogeintrag fortgeführt werden.

Fortsetzung folgt

QUELLEN

  • Avicenna, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
  • Digital Averroes Research Environment
  • Nicholas Rescher (1928 – ),The Development of Arabic Logic. University of Pittsburgh Press, 1964
  • Stanford Encyclopedia of Philosophy, Aristotle’s Logic
  • Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7

Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER.

AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 11

Abstraktion, Affirmativ, Ausdruck, Ausdruck - einfacher, Ausdruck - sprachlicher, Ausdruck - zusammengesetzter, Aussage, Aussagetypen, Außenwelt, Avicenna, Logik, Logik - Alltag, Logik - Antike, Logik - formale, Objekt, Objekt - als Eigenschaft, Objekt - echtes, Objekt erkanntes, Objekt-Modell, Philosophie - Islamische, Prädikat, Quantor, Subjekt, Wahrheit, Wahrheitswert, Wahrnehmen, Wahrscheinlichkeit
Bildskizzen zu Avicennas Diskussion der Aussagetypen Disjunktive und Konjuntive Konditionale
Bildskizzen zu Avicennas Diskussion der Aussagetypen Disjunktive und Konjuntive Konditionale

VORGESCHICHTE

Für einen Überblick zu allen vorausgehenden Beiträgen dieser rekonstruierenden Lektüre von Avicennas Beitrag zur Logik siehe AVICENNAS ABHANDLUNG ZUR LOGIK – BLITZÜBERSICHT.

Aufgrund des großen Umfangs enthält dieser Blogeintrag zu Avicennas Logik – im Gegensatz zu den vorausgehenden Blogeinträgen 1-9 – nur den Diskussionsteil von Blogeintrag 10. In Blogeintrag 10 wurde weiter die Position Avicennas beschrieben. Ziel der Lektüre ist die Rekonstruktion einer möglichen Theorie der Alltagslogik, wie sie dann in künstlichen lernenden Systemen eingesetzt werden soll (hier trifft die Philosophie direkt auf die Ingenieurskunst ….; man nennt dies ‚Informatik‘).

DISKUSSION

26. Wie schon mehrfach bemerkt, erscheint die Verwendungsweise der meisten Begriffe in Avicennas Abhandlung über die Logik ‚fließen‘ oder – mit einem Begriff aus der modernen Logik – ‚fuzzy‘.

27. Dies hat damit zu tun, dass Avicenna für die Verwendung seiner Begriffe keine klaren Kriterien benutzt. Typisches Beispiel ist sein Begriff der ‚Harmonie‘, den er für die Klassifikation von Antezedenz – Konsequenz Verhältnisse benutzt. Klar ist, dass er für diesen Begriff auf die Bedeutungsdimension zurückgreift; unklar ist, wie genau er dies versteht, da das, was er praktisch überall als ‚Bedeutung unterstellt‘, nirgendwo präzisiert wird. Will man diesen Nachteil beheben, muss man einen Weg finden, die Kriterien zu klären. Ein erprobtes Mittel dafür ist, alle die Umstände explizit zu machen, zu benennen, die man als für ein Kriterium ‚relevant‘ erachtet. Dies ist in der modernen Wissenschaft eine Mischung aus kontrollierten Beobachtungen und theoretischen Annahmen. Und da keine Beobachtung einen ‚Sinn‘ ergibt ohne Bezug zu vorausgesetzten Beziehungen/ Relationen/ Strukturen/ Modellen beginnt jede Klärung eines vagen Zusammenhangs mit ersten ‚theoretischen Annahmen‘ darüber, welche Zusammenhänge man für wichtig hält, mit denen man bekannte – oder noch zu messende – Phänomene ‚erklären‘ möchte.

28. Beginnen wir mit den letzten Annahmen von Avicenna.

AUSSAGEN – AUSSAGESTRUKTUREN

29. Ausgangspunkt sind solche Ausdrücke E, die ‚wahr‘ oder ‚falsch‘ sein können; er nennt sie ‚Aussagen‘ [PROP]: $latex PROP \subseteq E$.
30. Aus logischer Sicht hat Avicenna bislang vier funktionale Rollen innerhalb einer Aussage unterschieden: ‚Subjekt‘, ‚Prädikat‘, ‚Aussageoperatoren‘ sowie ‚Quantoren‘.
31. Minimal benötigen wir ‚Subjekt‘ S und ‚Prädikat‘ P, so dass man im Prädikat P etwas über das Subjekt S aussagen kann: $latex (S P)$
32. Zusätzlich gibt es die Rolle der logischen ‚Aussage-Operatoren‘ ‚Negation‘ $latex \neg$, ‚Exklusive Disjunktion‘ (auch ‚Kontravalenz‘ oder ‚X-OR‘) $latex \sqcup$, und ‚Quantoren‘ Q. Hier unterscheidet er Quantoren über die ‚Anzahl‘ $latex Q_{q}$, und Quantoren über die ‚Zeit‘ $latex Q_{t}$. Man solle gleich noch die Quantoren über den ‚Raum‘ $latex Q_{s}$ ergänzen; diese erwähnt er nicht explizit, aber im Bereich des Bedeutungsraumes spielt die Dimension des Raumes eine wichtige Rolle und begegnet uns in sehr vielen Aussagen.
33. Bei der Verwendung von Quantoren bezieht man sich immer auf eine Gesamtheit. Im Falle von Zeit-Quantoren $latex Q_{t}$ sind dies Zeitpunkte angeordnet auf einem Zeitstrahl. Im Falle von Anzahl-Quantoren $latex Q_{q}$ bezieht man sich auf die Objekte, zu denen das Subjekt einer Aussage in einer Beziehung steht; im Falle von Raum-Quantoren $latex Q_{s}$ bezieht man sich auf zu definierende ‚Raumstellen‘.
34. Unter der Voraussetzung, dass eine Aussage A = (S P) ‚wahr‘ oder ‚falsch‘ sein kann, kann man sagen, dass $latex \neg A$ ‚wahr‘ ist, wenn ‚A‘ alleine ‚falsch‘ ist, d.h. wenn die Aussage A= (S P) nicht zutrifft; d.h. $latex (S \neg P)$ trifft zu.
35. Die Aussage ‚Entweder A oder B‘ $latex (A \sqcup B)$ ist ‚wahr‘, wenn entweder A wahr und B falsch ist oder B wahr und A falsch. Die Verneinung von $latex \neg(A \sqcup B)$ ist wahr, wenn entweder A und B zusammen wahr oder zusammen falsch sind.
36. Die Aussage ‚Wenn A dann B‘ $latex (A \rightarrow B)$ ist nur dann falsch, wenn A zutrifft und zugleich B falsch ist. In allen anderen Fällen ist die Implikation wahr. Die Verneinung $latex \neg(A \rightarrow B)$ wäre dementsprechend wahr, wenn A wahr wäre und B nicht; in allen anderen Fällen falsch
37. Es sei angemerkt, dass die Implikation $latex (A \rightarrow B)$ äquivalent ist zu $latex \neg(A \wedge \neg B)$, wobei das Zeichen ‚$latex \wedge$‘ den aussagenlogischen Operator ‚Konjunktion‘ (‚und‘) repräsentiert. $latex (A \wedge B$ sind nur wahr, wenn A und B zugleich wahr sind, sonst falsch.
38. Quantoren werden Aussagen vorangestellt, also (Q A) bzw. (Q (S P)).
39. Anzahl-Quantoren $latex Q_{q}$ wären ‚alle‘ und verneint $latex \neg Q_{q}$ ’nicht alle‘, definiert durch ‚einige := nicht alle‘.
40. Zeit-Quantoren $latex Q_{t}$ wären ‚immer‘ und verneint $latex \neg Q_{t}$ ’nicht immer‘, definiert durch ‚manchmal := nicht immer‘.
41. Raum-Quantoren $latex Q_{s}$ wären ‚überall‘ und verneint $latex \neg Q_{s}$ ’nicht überall‘, definiert durch ‚einige := nicht überall‘.
42. Als Schreibweisen hat sich herausgebildet, im Falle von ‚alle’/ ‚immer’/ ‚überall‘ von ‚All-Quantoren‘ zu sprechen und zu schreiben $latex \forall(x)$. Das ‚x‘ steht dann für die Art von Objekten, über deren Gesamtheit quantifiziert wird. Im Fall von ‚einige’/ ‚manchmal“ spricht man von ‚Partikularquantoren‘ (missverständlich auch ‚Existenzquantoren‘) und schreibt $latex \exists(x)$. Das ‚x‘ steht wieder für die Art von Objekten, über deren Gesamtheit quantifiziert wird.
43. Im Falle von Partikularquantoren von ‚Existenzquantoren‘ zu sprechen ist leicht irreführend, da ein Existenzquantor $latex \exists(x)$ keine Aussage über die reale Existenz in der umgebenden Welt W trifft, sondern nur angibt, über wie wieviele Objekte x einer Art gesprochen werden soll.
44. Beispiel: ‚Manchmal ist der Himmel grau‘ $latex \exists(t)(der Himmel)(t)(ist grau)$. Es gibt einige Zeitpunkte t (aus der Gesamtheit der geordneten Zeitpunkte T), an denen vom Himmel gesagt werden kann, dass er grau ist.
45. Beispiel: ‚Überall scheint die Sonne‘ $latex \forall(s)(die Sonne)(scheint)$. An allen Raumpunkten s (aus der Gesamtheit der Raumpunkte S), kann von der Sonne gesagt werden kann, dass sie scheint.
46. Beispiel: ‚Alle Menschen sind sterblich‘ $latex \forall(x)(Menschen)(sind sterblich)$. Für alle Objekte aus der Gesamtheit der Menschen kann gesagt werden, dass sie sterblich sind.
47. Beispiel: ‚Nicht alle Menschen sind sterblich‘ $latex \neg\forall(x)(Menschen)(sind sterblich)$ wird übersetzt $latex \exists(x)(Menschen)(sind nicht sterblich)$, $latex \exists(x)(S)(\neg P)$, d.h. für einige Objekte aus der Gesamtheit der Menschen kann gesagt werden, dass sie nicht sterblich sind.

WAHRHEITSBEDINGUNGEN – BEDEUTUNGSRAUM

48. Mit der Einführung der Begriffe ‚Aussage‘, ‚Subjekt‘, ‚Prädikat‘, ‚Aussage-Operator‘, ‚Quantor‘ wurden Strukturelemente von Ausdrücken beschrieben. Allerdings wurde bei der ‚Charakterisierung‘ der unterschiedlichen logischen Rollen immer schon – mehr oder weniger explizit – Bezug genommen auf einen unterstellten ‚Bedeutungsraum‘ M.
49. Der wichtige Punkt hier ist, dass man den Unterschied zwischen dem Bedeutungsraum M und den Eigenschaften X der umgebenden Welt W beachtet.
50. Wie schon zuvor herausgestellt, ist der Bedeutungsraum M, auf den sich die Aussagen mit ihren Strukturen primär beziehen, zu einem gewissen Teil eine Konstruktion über bestimmten Ereignissen X in der umgebenden Welt W.
51. Dieser Unterschied ist die Voraussetzung für Begriffe wie z.B. ‚Existenz‘, ‚wahr’/ ‚falsch‘ und ‚möglich‘.
52. Denn mittels einer Aussage A bestimmte Bedeutungselemente $latex m \subseteq M$ zu benennen, zu aktivieren, ist zwar eine Grundvoraussetzung dafür, dass ein Ausdruck e als Aussage A überhaupt eine ‚Bedeutung‘ hat, diese Bedeutungselemente m sind als solche aber weder ‚wahr‘ noch ‚falsch‘; ihre ‚Existenz‘ ist unklar; ob sie ‚real‘ oder ‚möglich‘ sind folgt aus der primären Bedeutung nicht.
53. Erst wenn man davon ausgeht, dass es innerhalb des Bedeutungsraumes M solche Bedeutungselemente m* gibt, die sich von anderen Bedeutungselementen m0 dadurch unterscheiden, dass ihnen ein ‚Aktualitätsbezug‘ zu aktuellen Wahrnehmungen zusprechen kann, nur dann kann es ein Kriterium geben, wodurch eine Aussage A ’nur‘ eine ‚wahrheitsneutrale‘ Bedeutung m0 hat oder eben durch die ‚Aktualitätseigenschaft‘ m* als ‚zutreffend in der umgebenden Welt M‘ charakterisiert werden kann. An dieser Eigenschaft des ‚aktuell Zutreffens‘ in der umgebenden Welt W lassen sich die Begriffe ‚wahr‘ und ‚falsch‘ ‚anhängen‘: gibt es eine Bedeutung m0, die eine hinreichende Ähnlichkeit mit einer Bedeutung m* hat, dann kann man von der Aussage, die die Bedeutung m0 bezeichnet, sagen, dass sie ‚zutrifft‘ und damit ‚wahr‘ ist; gibt es zu einer aktuell bezeichneten Bedeutung m0 einer Aussage A keine hinreichend ähnliche Bedeutung m*, dann trifft die Bedeutung m0 der Aussage A nicht zu, d.h. sie ist falsch.
54. Sofern wir über ‚Erinnerungen‘ an Bedeutungen m(m*) verfügen, die zu ‚vorausgehenden Zeitpunkten‘ einmal ‚wahr‘ waren, kann dieses Wissen m(m*) dazu benutzt werden, um eine ‚Erwartung‘ über die umgebenden Welt W aufzubauen, dass der Sachverhalt m(m*) sich als aktuelle Wahrnehmung m* ‚reproduzieren‘ lässt; dafür, dass dem so ist, gibt es keine ‚Garantie‘; selbst die sogenannten ‚Naturgesetze‘ sind keine 100%ige Garantie dafür, dass eine erinnerbare Eigenschaft m(m*) aufgrund ihres ‚früheren‘ Auftretens als m* nochmals als m* auftreten wird.

MÖGLICH

55. Ich würde den Begriff der Möglichkeit auch an dieser Differenz aufhängen: einerseits ‚aktuell wahrgenommene‘ Bedeutungselemente m* bzw. ‚erinnert als schon mal aktuell wahrgenommen‘ m(m*)‘ und andererseits nur ‚gedacht’/ ‚vorstellbar‘ als m0 ohne Entsprechung zu einem m* bzw m(m*). Eine ‚Differenz‘ zwischen allgemein vorstellbar/ denkbar und aktuell wahrnehmbar bzw. erinnert als aktuell mal wahrgenommen ist generell ein Hinweis auf Möglichkeit. Wie ‚wahrscheinlich‘ solche möglichen Bedeutungselemente m0 mal als m* reproduziert werden können, ist allgemein kaum anzugeben. Basierend auf dem bislang verfügbaren erinnerbaren Wissen M(M*) insgesamt kann man zwar gewisse ‚Erwartungen‘ konstruieren; dies können aber – wie wir aus der Geschichte wissen – unzuverlässig sein, da sie auf falschen Annahmen bzw. Interpretationen beruhen können (‚Sonne bewegt sich um die Erde‘ oder ‚Erde bewegt sich um die Sonne‘).

WELT ALS FIKTION

56. Aus der bisherigen Rekonstruktion folgt, dass der Begriff der ‚umgebenden Welt W‘ streng genommen eine ‚Fiktion‘ ist. Was es gibt, sind Erregungszustände m* im Gehirn, die es zum überwiegenden Teil nicht selbst verursacht; sie werden in die Erregungsmenge des Gehirns ‚induziert‘. Verglichen damit sind die anderen (bewussten) Erregungszustände m0 ‚von innen‘ (endogen) erzeugt. Unser Gehirn nimmt diese nicht-selbst induzierten (bewussten) Erregungszustände m* als ‚etwas von ihm Verschiedenes‘, an dem sich viele ‚Eigenschaften‘ unterscheiden lassen, u.a. auch eine implizite Raumstruktur. Der Begriff der ‚Welt‘ ist in diesen nicht-selbst induzierten Erregungszuständen m* fest gemacht. Als m* sind diese Erregungszustände ‚unmittelbar‘, ‚direkt‘, so, als ob wir die ‚Welt‘ ‚direkt‘ erleben würden. Wie wir aber heute wissen (können), sind diese direkt erlebbaren Erregungszustände m* das ‚Produkt‘ eines komplizierten Übersetzungsmechanismus, den wir sinnliche Wahrnehmung perc() nennen. Im Prozess der sinnlichen Wahrnehmung perc() werden einige der Weltereignisse X in sinnliche Zustände $latex m_{p}$ abbgebildet: $latex perc: X \longrightarrow M_{p}$. Zusätzlich wissen wir heute, dass die schon verfügbaren Bedeutungselemente M auf diesen Wahrnehmungsprozess Einfluss nehmen können (Stichwort ‚Erwartungen‘, ‚Vorurteile‘ , …): $latex perc: X \times M \longrightarrow M_{p}$.
57. Dabei sind es normalerweise nicht die sinnlichen Erregungszustände $latex M_{p}$, die wir wahrnehmen, sondern die Objekte der nächsten Verarbeitungsstufe, die aus den sinnlichen Elementen als Objektelemente heraus abstrahiert werden: $latex \alpha: M_{p} \times M \longrightarrow M_{o}$. Auch hier wirken sich die schon vorhandenen Bedeutungselemente M auf den Abstraktionsprozess aus. Statt $latex M_{o}$ wird hier auch verkürzend oft nur von den ‚Objekten‘ O gesprochen, da Objekte immer nur als Elemente des Bedeutungsraumes M vorkommen.
58. Die zuvor erwähnten aktuellen Wahrnehmungen m* sind eine Teilmenge der Objektelementen $latex M_{o}$, also $latex m* \subseteq M_{o}$. Die Objektelemente ohne die aktuellen Wahrnehmungen m* gehören zu den ‚denkbaren‘ Objektelementen, also $latex (M_{o} – m*) \subseteq M0$. Dies ist möglich, weil im Gehirn ja nicht ‚reale‘ Objekte mit ‚gedachten‘ Objekten verglichen werden, sondern die ‚realen‘ Objekte treten im Gehirn schon als ‚gezähmte‘ Objekte auf, d.h. was immer an Eigenschaften X in der realen Welt W zur Konstruktion der aktuellen Wahrnehmungen m* geführt hat, m* selbst ist ein Konstrukt wie m0 auch. Deswegen lassen sich beide ‚vergleichen‘ und mit den Mitteln des ‚Denkens‘ ‚bearbeiten‘.

ERGEBNISSE

59. An dieser Stelle könnte man jetzt eine eigene große Abhandlung zur Alltagslogik schreiben. Um den Gang der weiteren Untersuchung von Avicennas Abhandlung damit aber nicht vollständig zu sprengen, beende ich hier die rekonstruierenden Überlegungen und wende mich wieder der Lektüre des Textes zu. Wie man sieht, kann solch eine Lektüre extrem anregend sein.

AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 10

Avicenna, Logik, Logik - Alltag, Logik - Antike, Logik - formale
Bildskizzen zu Avicennas Diskussion der Aussagetypen Disjunktive und Konjuntive Konditionale
Bildskizzen zu Avicennas Diskussion der Aussagetypen Disjunktive und Konjuntive Konditionale

VORGESCHICHTE

Für einen Überblick zu allen vorausgehenden Beiträgen dieser rekonstruierenden Lektüre von Avicennas Beitrag zur Logik siehe AVICENNAS ABHANDLUNG ZUR LOGIK – BLITZÜBERSICHT.

Dieser Blogeintrag beginnt mit einer Darstellung der Position von Avicenna und diskutiert dann im Abschnitt ‚DISKUSSION‘ Avicennas Position. Ziel der Lektüre ist die Rekonstruktion einer möglichen Theorie der Alltagslogik, wie sie dann in künstlichen lernenden Systemen eingesetzt werden soll (hier trifft die Philosophie direkt auf die Ingenieurskunst ….; man nennt dies ‚Informatik‘).

AVICENNAs DISKUSSION DES DISJUNKTIVEN UND DES KONJUNKTIVEN KONDITIONALS

1. Anstatt jetzt einzelne Stellen aus dem Text (SS.24-27) zu zitieren hier eine reflektierende Zusammenfassung seiner Aussagen.

AUSDRÜCKE, DIE AUSAGEN SIND

2. Der übergreifende Zusammenhang seiner Überlegungen bilden solche Ausdrücke, die als ‚Aussagen‘ bestimmte Sachverhalte beschreiben, die ‚wahr‘ oder ‚falsch‘ sein können.

3. Das grundsätzliche Kennzeichen solcher Aussagen ist, dass sie von etwas ‚affirmierende‘ (zustimmend, bekräftigend, …) sagen, dass es sich so verhalte, wie gesagt.

QUANTOR SUBJEKT PRÄDIKAT (Q S P)

4. Eine Aussage kann man entweder mit ‚grammatischen‘ Begriffen analysieren im Sinne von ‚Name Verb Präposition Name‘ (z.B. ‚Zyd ist im Haus‘) oder mit logischen Begriffen wie ‚Quantor Subjekt Prädikat‘ (Q S P).

5. Das Subjekt S ist dasjenige, von dem/ über das etwas ausgesagt wird, das im Prädikat P formuliert wird. Der Quantor Q klärt, ob es ‚universell‘ (z.B. ‚alle‘) gemeint ist oder ‚partikulär‘ (z.B. ’nicht alle‘ als ‚einige‘).

EXISTENZ

6. Avicenna benutzt auch bisweilen den Begriff ‚Existenz’/ ‚existieren‘ im Kontext, dass der Sachverhalt einer Aussage ‚existiert‘ oder ’nicht existiert‘, ohne die Verwendung des Begriffs ‚existieren‘ explizit zu analysieren.

EXISTENZ, AFFIRMATION, VERNEINUNG

7. Das Wechselspiel zwischen den Begriffen ‚Affirmieren/ Affirmation‘, ‚Verneinung‘ sowie ‚Existenz‘ ist nicht ganz klar. Einerseits kann die Verneinung eines Sachverhaltes (S nicht P) dennoch eine Affirmation sein, d.h. der Sprecher will damit sagen, dass es zutrifft, dass nicht-P auf S zutrifft, andererseits wird die Verneinung manchmal so verwendet, als ob damit grundsätzlich die Affirmation aufgehoben würde. Einerseits wird ein Ausdruck der Art (S nicht P) interpretiert, dass das ’nicht-P‘ existiert als Eigenschaft von S, dann aber wieder soll das ’nicht‘ in P die ‚Existenz von P‘ aufheben.

BESTIMMT – UNBESTIMMT

8. Auch benutzt Avicenna den Begriff ‚bestimmt/ nicht bestimmt‘ im Kontext der Verwendung von Quantoren. So sagt er z.B. dass (Alle S sind P) ‚bestimmt‘ sei in der Bedeutung, (Nicht-Alle S sind P) aber ’nicht bestimmt‘ als ‚unbestimmt‘. Auch im Kontext der Verwendung von logischen Operatoren (siehe unten) taucht dieses Begriffspaar nochmals auf.

DISJUNKTIVE UND KONJUNKTIVE KONDITIONALE

9. Damit kommen wir zum Hauptthema dieses Abschnitts: ‚Disjunktive und Konjunktive Konditionale‘.

10. Was ein disjunktives oder ein konjunktives Konditional ist erklärt er nicht durch eine explizite Definition innerhalb einer Theorie, sondern durch Beispiele von Ausdrücken, die er (mittels impliziter semantischer Kriterien) so oder so charakterisiert/ klassifiziert.

11. Grundbausteine bleiben die Aussagen (Q S P), die wahr oder falsch sein können. Solche Aussagen kann man auch mit Buchstaben ‚A‘, ‚B‘ abkürzen, was Avicenna selbst im vorausgehenden Text einmal getan hat. Dabei gibt es zwei Fälle: (i) Aussagen ohne Quantoren wie A=(S P) (z.B. ‚Zid lacht‘), oder (ii) Aussagen mit Quantoren A=(Q S P) (z.B. ‚Alle Menschen sind sterblich‘).

QUANTOREN: ANZAHL – ZEIT

12. Er führt dann zwei Arten von logischen Quantoren ein: (i) (Entweder … Oder …) bzw. (ii) (Wenn … dann …). Fall (i) nennt er ‚Disjunktives Konditional‘ und Fall (ii) ‚Konjunktives Konditional‘ (in der späteren modernen Aussagelogik versteht man unter ‚Konjunktion‘ etwas anderes; Fall (ii) von Avicenna heißt in der modernen Aussagenlogik ‚Exklusives Oder‘ oder ‚Kontravalenz‘). Eine moderne Schreibweise für (Wenn A dann B) wäre ($latex A \rightarrow B$), und für (Entweder A oder B) die Schreibweise ($latex A \sqcup B$)).

HARMONIE – DISHARMONIE

13. Interessant ist, dass Avicenna seine logischen Operatoren nicht mit Hilfe sogenannter Wahrheitstafeln (Wahrheitsfunktionen) explizit charakterisiert, sondern aus einer Mischung von Wahrheitswertzuordnungen und den Begriffen ‚Harmonie/ Disharmonie‘.

ANTEZEDENZ – KONSEQUENZ

14. Dazu benötigt er noch zwei Zusatzbegriffe, nämlich die Begriffe ‚Antezedenz‘ und ‚Konsequenz‘. Im Beispiel (Wenn A dann B) kann man nach Avicenna das ‚A‘ als Antezedenz‘ von der Konsequenz ‚B‘ sehen. Im Beispiel (Entweder A oder B) ist es eigentlich nicht klar, welche Komponente das Antezedenz sein soll. Avicenna optiert dafür, dass der ‚linke Teil‘, also ‚Entweder A‘ ein Antezedenz sei, gesteht aber zu, dass es in diesem Fall viele Konsequenzen geben könnte, also (Entweder A oder B1 oder B2 …).

15. Kombiniert mit den Begriffen ‚Harmonie’/ ‚Disharmonie‘ befinden sich die Ausdrucksteile ‚A‘ und ‚B‘ im Fall (Wenn A dann B) in ‚Harmonie‘ (‚Wenn‘ (‚die Sonne‘ ‚aufsteigt‘), ‚dann‘ (‚es‘ ‚ist‘ Tag‘)). B soll hier nach Avicenna von A abhängen. Zu sagen (Wenn (‚es‘ ‚ist‘ ‚Tag‘) dann (‚die Sonne‘ ’steigt auf‘)) würde nach Avicenna disharmonisch sein. Im Falle einer Disjunktion (Entweder A oder B) sei dies aber nicht so. Zwischen dem Antezedenz ‚A‘ und den verschiedenen möglichen Konsequenzen ‚B1‘, ‚B2‘, … besteht keine Harmonie; man kann ihre Anordnung im Ausdruck ändern, ohne dass sich der gemeinte Sachverhalt ändert.

16. Unklar bei Avicenna ist allerdings, ob man nur innerhalb der Konsequenzen ‚B1‘, ‚B2’… umstellen kann bei Beibehaltung des ‚A‘ als Antezedenz oder ob man generell umstellen könnte, also (Entweder ‚B3‘ oder ‚B1‘ oder ‚A‘ oder …).

17. Generell ist die Verwendungsweise der logischen Begriffe bei Avicenna durchgehend ‚fließend‘, d.h. aufgrund seiner generell vagen Charakterisierungen der Begriffe kommt es ständig zu ‚Vermischungen‘ von Verwendungsweisen, die ‚verwirren‘ können. So stellt er einmal die Frage, wie denn das Verhältnis der Begriffe ‚Antezedenz – Konsequenz‘ zu den Begriffen ‚Subjekt S – Prädikat P‘ sei. Würde man berücksichtigen, dass die Begriffe ‚S- P‘ die ‚innere Struktur‘ eines Ausdrucks analysieren, der eine Aussage ist, und die Begriffe ‚Antezedenz‘ – ‚Konsequenz‘ das Verhältnis zwischen Aussagen analysieren, dann würde man diese Frage gar nicht stellen. Die Tatsache aber, dass Avicenna diese Frage aufwirft, zeigt, dass er für sich diese Verwendungsweisen nicht so klar abgegrenzt hat.

18. So kommt Avicenna zu der Deutung, dass in einem Ausdruck der Art (Wenn A dann B) die Verbindung von ‚Wenn‘ mit ‚A‘ aus der Aussage A (die wahr oder falsch sein kann), mit ‚Wenn A‘ ein Ausdruck entsteht, der nicht mehr wahr oder falsch sein kann und daher keine eigentliche Aussage mehr ist. Das gleiche gelte für das Konsequenz ‚dann B‘; auch wenn ‚B‘ für sich wahr oder falsch sein kann, in der Kombination ‚dann B‘ ist der neue zusammengesetzte Ausdruck weder wahr noch falsch und damit keine Aussage.

19. Auf den ersten Blick hat Avicenna Recht, da die beiden Ausdrücke ‚Wenn A‘ und ‚dann B‘ isoliert voneinander, nach den bisherigen Regeln keinen Wahrheitswert haben können. Aber das ‚Wesen‘ eines zusammengesetzten Ausdrucks, dessen Teile über logische Operatoren verbunden sind, besteht ja gerade darin, dass sich der Wahrheitswert des zusammengesetzten Ausdrucks aus den Wahrheitswerten der Teilausdrücke ergeben soll, vorausgesetzt, alle Teilausdrücke sind jeweils für sich Aussagen. Also im Ausdruck (Wenn A dann B) wäre der Wahrheitswert des gesamten Ausdrucks zu berücksichtigen, nicht seiner isolierten modifizierten Teile ‚Wenn A‘ bzw. ‚dann B‘.

20. Avicenna selbst bemerkt, dass der Zusammenhang zwischen (S P) in einer Aussage A=(S P) verschieden ist von dem Zusammenhang von Aussagen in einem zusammengesetzten logischen Ausdruck (Entweder A oder B). Während in der Aussage A das Prädikat P etwas über das Subjekt S aussagt, muss zwischen der Aussage B und der Aussage A in (Entweder A oder B) inhaltlich kein Zusammenhang bestehen. Dennoch bleibt er bei seinen ‚fließenden‘ Verwendungsweisen.

ZEITQUANTOREN

21. Innovativ erscheint seine Benutzung von ‚Quantoren über die Zeit‘. Bislang hatte er ‚Quantoren über die Anzahl‘ benutzt wie ‚alle‘ und ’nicht alle’/ ‚einige‘.

22. Quantoren über die Anzahl: Eine Aussage (alle S sind P) mit dem Quantor Q=’alle‘ nennt er ‚universell‘; eine Aussage (nicht alle S sind P) mit dem Quantor Q=’nicht alle‘ nennt er ‚partikulär‘ (und qualifiziert sie als ‚unbestimmt‘ bzgl. des Wahrheitswertes).

23. Bei Quantoren über die Zeit setzt er implizit eine Art Folge von Zeitpunkten T voraus, so dass man von zwei Zeitpunkten (t,t‘) immer sagen kann, ob t ‚früher‘, ‚gleich‘ oder ’später‘ zu t‘ ist. Ein möglicher Zeitquantor könnte sein ‚immer‘ bzw. ’nicht immer‘ als ‚manchmal‘.

24. Behält man die Struktur (Q S P) bei mit A=(S P) und (Q A), dann gibt es jetzt im Fall von zusammengesetzten logischen Aussagen wieder zwei Möglichkeiten: Entweder (i) die Quantoren sind an die einzelnen Aussagen gebunden (z.B. ‚Wenn (Q A) dann (Q B)‘) oder sie erstrecken sich über mehr als eine Aussage (z.B. ‚Q Wenn A dann B). Avicenna scheint nur den Fall (ii) zu berücksichtigen. Ein Beispiel: (Q Wenn A dann B) als ‚Manchmal Wenn A dann B‘ mit A=’Die Sonne geht auf‘, B=’Es gibt Wolken‘.

DISKUSSION

Wegen des großen Umfangs habe ich die Diskussion dieser Überlegungen von Avicenna in einen nächsten Blogeintrag ausgelagert.

Zur Fortsetzung bitte hier klicken.

QUELLEN

  • Avicenna, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
  • Digital Averroes Research Environment
  • Nicholas Rescher (1928 – ),The Development of Arabic Logic. University of Pittsburgh Press, 1964
  • Stanford Encyclopedia of Philosophy, Aristotle’s Logic
  • Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7

Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER.

AVICENNAS ABHANDLUNG ZUR LOGIK – BLITZÜBERSICHT

Allgemein, Allquantor, Alltagssprache, Analytisch, Annahme, Art (Spezies), Ausdruck, Ausdruck - einfacher, Ausdruck - sprachlicher, Ausdruck - zusammengesetzter, Aussage, Aussagetypen, Außenraum zum Körper, Außenwelt, Avicenna, Bedeutung, Bedeutung - akzidentell, Bedeutung - empirisch, Bedeutung - kontingent, Bedeutung - wesentliche, Bedeutung eines Wortes, Bedeutungsbeziehung, Bedeutungskorrelat, Bedeutungsraum, Begriffe, Definiendum, Definiens, Definition, Definition - explitite, Definition - rekursive, Definition - simultane, Denken, Eigenschaft, Erinnerung, Evolution - biologische, Evolution - kognitive, Externe Welt, Folgern - logisches, Folgerung, Logik, Logik - Alltag, Logik - Antike, Logik - formale, Prädikat, Prämisse, Subjekt, Subjekt - logisches, Syllogismus, Syllogismus - Konjunktiver, Term

(Letzte Änderung 14.Okt.2014, 06:11h )

Da die rekonstruierende Lektüre zu Avicennas Abhandlung zur Logik ein immer größeres Ausmaß annimmt, erweist sich die Methode, jeden einzelnen Beitrag mit einem Überblick über die vorausgehenden Beiträge einzuleiten, als immer weniger praktikabel. Deswegen wird jetzt ein eigener Blogeintrag als Referenzpunkt für diesen Überblick gewählt. Dies bedeutet, dass künftig alle nachfolgenden Beiträge einleitend (für die ‚Vorgeschichte‘), auf diesen Blogeintrag verweisen werden. Es ist zu beachten, dass diese Übersicht nur eine Übersicht über die wichtigsten Begriffe und Themen ist ohne alle Details und normalerweise auch ohne die ausführliche Diskussion von Avicennas Gedanken. Diese finden sich nur in den Blogeinträgen selbst, auf die verwiesen wird.

1. In einem ersten Beitrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 1 hatte ich geschildert, wie ich zur Lektüre des Textes von Avicenna gekommen bin und wie der Text grob einzuordnen ist.

2. In einem zweiten Beitrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 2 ging es um die Frage, warum überhaupt Logik? Avicenna führt erste Unterscheidungen zu verschiedenen Wissensformen ein, lässt aber alle Detailfragen noch weitgehend im Dunkeln.

3. Im Teil AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 3 ging es um einfache und zusammengesetzte Begriffe, und bei den einfachen Begriffen um ‚individuelle‘ und ‚universelle‘. Schon hier zeigt sich der fundamentale Unterschied zwischen der antiken und der modernen-formalen Logik. In der antiken Logik wird die Ausdrucksebene E – und einer sich daran manifestierenden Folgerungslogik – immer in Verbindung mit einer zugehörigen Bedeutungsstruktur gesehen, die sich an einer Objektstruktur O festmacht. Die moderne formale Logik kennt zwar auch ‚Semantiken‘ und ‚Ontologien‘, diese sind aber ’sekundär‘, d.h. es werden nur solche ‚formalen Semantiken‘ betrachtet, die zum vorausgesetzten syntaktischen Folgerungsbegriff ‚passen‘. Dies sollte dann später an konkreten Beispielen diskutiert werden. Hier liegt der Fokus auf der antiken Logik im Sinne Avicennas.

4. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 4 knüpft Avicenna an den zuvor eingeführten Begriff des ‚universellen‘ Begriffs an und betrachtet jetzt solche als ‚universell‘ bezeichneten Ausdrücke in einem Ausdruckskontext von aufeinanderfolgenden Ausdrücken. Alle diese Ausdrücke könnte man im Sinne der antiken Logik auch als ‚Urteile‘ bezeichnen, durch die einem bestimmten Ausdruck durch andere Ausdrücke bestimmte Bedeutungen (Eigenschaften) zu- oder abgesprochen werden. Hier unterscheidet er die Fälle eines ‚wesentlichen‘ Zusammenhanges zwischen zwei Begriffen und eines ’nicht wesentlichen‘ – sprich ‚akzidentellen‘ – Zusammenhangs.

5. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 5 führt Avicenna eine Reihe von neuen technischen Begriffen ein, die sich nicht alle in ihrer Bedeutung widerspruchsfrei auflösen lassen. Es handelt sich um die Begriffe ‚Genus‘, ‚Spezies‘, Differenz, allgemeine und spezielle Akzidens, den Begriff ‚Kategorie(n)‘ mit den Kategorien ‚Substanz‘, ‚Qualität‘ und ‚Quantität‘. Die Rekonstruktion führt dennoch zu spannenden Themen, z.B. zu einem möglichen Einstieg in das weltverändernde Phänomen der kognitiven Evolution.

6. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 6 geht es um die Begriffe ‚Definition‘ und ‚Beschreibung‘. Im Verhältnis zwischen beiden Begriffen geht die Beschreibung der Definition voraus. In der ‚Definition‘, die Avicenna vorstellt, wird ein neuer Ausdruck e mittels anderer Ausdrücke <e1, …, ek>, die sich auf schon bekannte Sachverhalte beziehen, ‚erklärt‘. Die von Avicenna dann vorgenommene Erklärung, was eine ‚Definition‘ sei, hängt u.a. stark ab von dem Begriff der ‚Bekanntheit‘ und dem Begriff des ‚wahren Wesens‘. Für die Tatsache, dass ein Mensch A bestimmte Ausdrücke <e1, …, ek> einer Sprache L ‚kennt‘ oder ’nicht kennt‘, dafür gibt es keine allgemeinen Regeln oder Kriterien. Von daher macht die Verwendung der Ausdrücke ‚bekannt’/ ’nicht bekannt‘ eigentlich nur Sinn in solch einem lokalen Kontexten W* (z.B. einem Artikel, ein Buch, ein Vortrag, …), in dem entscheidbar ist, ob ein bestimmter Ausdruck e einer Sprache L schon mal vorkam oder nicht. Schwierig wird es mit dem Begriff des ‚wahren Wesens‘. In meiner Interpretation mit der dynamischen Objekthierarchie gibt es ‚das wahre Wesen‘ in Form von Objekten auf einer Stufe j, die Instanzen auf Stufen kleiner als j haben. Dazu gab es weitere Überlegungen.

7. Im folgenden Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 7 beschreibt Avicenna syntaktisch zusammengesetzte, aber semantisch einfache Ausdrücke. Innerhalb der Ausdrücke unterscheidet er die Teileausdrücke ‚Name‘, ‚Verb‘ und ‚Präposition‘. Die unterschiedliche Charakterisierung erfolgt nicht aufgrund der syntaktischen Form, sondern aufgrund der semantischen Eigenschaften, die mit diesen Ausdrücken verbunden werden. Neben dem Objektbezug, der die eigentliche Bedeutung fundiert, gibt es im Bedeutungsraum auch noch den zeitlichen und den räumlichen Aspekt. Das Zusammenspiel von Bedeutung und Ausdruck wird angerissen.

8. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 8 geht es um solche Ausdrücke E, die ‚Aussagen‘ P sind, von denen man sagt, dass sie ‚wahr‘ oder ‚falsch‘ seien. Aussagen sind eine echte Teilmenge aller Ausdrücke, $latex P \subset E$. Avicenna unterscheidet drei Arten von Aussagen: ‚kategorische‘ Aussagen, ‚Disjunktiv-konditionelle‘ und ‚Konjunktiv-konditionelle‘. Es wird ausführlich eine mögliche Wahrheitstheorie für die Zuschreibung ‚wahr’/ ‚falsch‘ diskutiert. Dann werden nochmals die Aussagetypen näher untersucht. Ein Zusammenhang mit der modernen Aussagenlogik wird hergestellt. Disjunktion, Konjunktion (und ergänzend) Implikation) sind Aussagetypen, die aus zwei Teilausdrücken A und B bestehen, die selbst wieder Aussagen sind, die wahr oder falsch sein können. Die beiden Teilausdrücke A und B werden dann durch die Teilausdrücke (oder), (und) sowie (wenn)-(dann)- verknüpft. Sie unterscheiden sich dadurch, wie der Wahrheitswert des Gesamtausdrucks von der Verteilung der Wahrheitswerte auf die Teilausdrücke festgelegt ist. Die Teilausdrücke (oder), (und) sowie (wenn)-(dann)- nennt man später dann auch ‚aussagenlogische Operatoren‘. Der Aussagetyp ‚kategorisierend‘ passt nicht in dieses Schema. Der Aussagetyp ‚kategorisierend‘ ist eine Aussage A, die wahr oder falsch sein kann unabhängig von irgendeinem aussagenlogischen Operator. Auch wird die Verneinung/ Negation diskutiert. Ausdrücke wie (Etwas)(ist nicht)(dies)(oder)(jenes) wurden rekonstruiert als $latex \neg(A)(oder)(B)$ mit dem Zeichen $latex \neg$ für ’nicht‘ oder ‚es ist nicht der Fall, dass‘.

9. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 9 kommt Avicenna auf mehrere Begriffspaare zu sprechen, die sich z.T. mit Themen berühren, die er schon vorher besprochen hat, z.T. neue Aspekte thematisieren, die nicht so ohne weiteres mit dem bisher Gesagten harmonieren. Es handelt sich z.B. um die Begriffe ‚Kategorisch‘, ‚Negation‘, ‚Universal‘, ‚Partikulär‘, die aber jetzt mit neuen Randbedingungen nochmals diskutiert werden. So stellt er die Frage, wann ‚kategorischen‘ (‚kategorisierenden‘) Aussagen ‚affirmativ‘ und wann sie ’negativ‘ sind. Ferner führt er neben den bisherigen die semantisch motivierten Begriffe ‚Name‘, ‚Verb‘ (auch ‚Term‘ genannt), sowie ‚Präposition‘ nun auch das Begriffspaar ‚Subjekt‘ und ‚Prädikat‘. Auch diese sind ’semantisch‘ motiviert, d.h. nur durch Rückgriff auf die Bedeutung kann man zur Klassifikation ‚Subjekt‘ bzw. ‚Prädikat‘ kommen. In den soeben erwähnten Kontexten wie auch in nachfolgenden Beispielen diskutiert Avicenna auch die Begriffe ‚affirmativ‘ und ’negativ‘. Zwischendrin bemerkt er auch mal, dass das Treffen einer Feststellung, eigentlich nur Sinne mache, wenn dasjenige, von dem etwas ausgesagt wird, auch existiere. Doch wird dieser Punkt nicht weiter diskutiert. Vom Subjekt einer Aussage sagt Avicenna, dass es partikulär‘ oder ‚universell‘ sein kann. Falls universell, dann kann man unterscheiden, ob sie ‚unbestimmt‘ (engl.: ‚indeterminate‘) ist – wie viele genau involviert sind — oder eben ‚bestimmt‘ (engl.: ‚determinate‘). Ferner illustriert er am Beispiel der kategorisierenden Aussagen auch die Begriffe ’notwendig‘ und ‚kontingent‘. Diese Verwendung der Begriffe stimmt überein mit den zuvor eingeführten Begriffe ‚wesentlich‘ und ‚akzidentell‘. Auch erwähnt Avicenna den Begriff ‚möglich‘. Er sieht mindestens zwei Verwendungsweisen von ‚möglich‘: In der Diskussion dieses Abschnitts werden einerseits einige Widersprüchlichkeiten in den Ausführungen Avicennas sichtbar gemacht, andererseits wird die Rekonstruktion einer möglichen systematischen Theorie zur Logik Avicennas fortgesetzt. Die wichtigsten Kritikpunkte kreisen um das Begriffspaar ‚affirmativ – negativ‘ mit der Kritik, dass beide Begriffe auf unterschiedlichen semantischen Ebenen liegen. Ferner widerspricht die Handhabung der Quantoren durch Avicenna der allgemeinen Verwendung.

10. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 10 diskutiert Avicenna seine Begriffe ‚Konjunktives‘ und ‚Disjunktives Konditional‘ unter verschiedensten Aspekten. Einige davon sind die Quantoren (wobei er auch Quantoren über die Zeit benutzt!), das Begriffspaar ‚Antezedenz – Konsequenz‘, der Begriff der ‚Harmonie‘, und wiederholt die Aspekte ‚Existenz‘, ‚Affirmation‘ sowie ‚Bestimmt/ Unbestimmt‘. Alle diese Aspekte werden in diesem Blogeintrag schon ein wenig ‚vorsortiert‘, um dann im nachfolgenden Blogeintrag weiter rekonstruierend diskutiert zu werden.

11. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 11 erfolgt eine ‚rekonstruierende Diskussion‘ von Avicennas Überlegungen aus Blogeintrag 10. Seine Überlegungen werden aufgegriffen und in einen theoretischen Rahmen eingeordnet, der es erlaubt, die Begriffe schärfer zu fassen und sie dadurch besser voneinander abzugrenzen. Nach einer Übersicht über die Struktur der Aussagen erfolgt dann eine Rekonstruktion von Bedeutungszuordnungen und eine Erklärung von Begriffen wie ‚wahr’/ ‚falsch‘, ‚Existenz‘, und ‚möglich‘.

12. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 12 diskutiert Avicenna den Fall widersprüchlicher Aussagen. Gemessen an dem bisher Gesagten bringt er in diesem Abschnitt keine neuen Aspekte ins Spiel. Wohl aber bietet dieser Abschnitt weitere Beispiele für sein Auffassung des Sachverhalts. Sie belegen, wie schwer er sich durchgängig damit tut, in dem unscharfen Wechselspiel von Ausdrucksseite und Bedeutungsseite eine konstante Verwendungsweise seiner Begriffe durchzuhalten. In diesem Blogeintrag erfolgt die Diskussion seines Textes immer unmittelbar hinter jedem Punkt in Form einer Anmerkung.

13. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 13 diskutiert Avicenna die Möglichkeit der Konvertierung von Aussagen mit Quantoren in solche, deren Bedeutung trotz Veränderung von Ausdruckselementen ‚erhalten‘ bleibt. In einigen Beispielen widerspricht er sich selbst; manche Stellen sind unklar. Es zeigt sich allgemein: (i) die Formulierung von Konvertierungsregeln greift beständig auf bestimmte unterstellte Bedeutungen zurück und (ii) genau diese unterstellten Bedeutungen werden nicht hinreichend klar definiert. Daraus entsteht die Forderung, diese unterstellte Bedeutung klar zu definieren und auf dieser Basis alle logischen Ausdruckselemente eindeutig zu definieren (was im nachfolgenden Abschnitt dann unternommen wird).

14/14b. In den Blogeinträgen AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 14 sowie AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 14b geht es darum, erstmalig einen theoretischen Rahmen für eine Semantik zu formulieren, mit der man die Logik Avicennas konsistent entwickeln kann. Abschnitt 14b stellt eine Überarbeitung des Eingangsteils von Abschnitt 14 dar. Es hat sich gezeigt, dass die in 14b gewählte Begrifflichkeit für das weitere Vorgehen ‚günstiger‘ wirkt. Aber wir befinden uns noch in der Phase der ‚Annäherung‘ an das ‚Neue‘.

15. In dem Blogeintrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 15 geht es um die Feinstruktur von Aussagen. Avicenna unterteilt ja Ausdrücke anhand inhaltlicher Kriterien nach Subjekt S, Prädikat P und ergänzend nach Quantoren Q. Es fragt sich, wie man diesen Ausdrucksteilen eine ‚Bedeutung‘ im Objektraum O zuordnen kann. Wichtig ist hier die schon früher getroffene Unterscheidung zwischen ‚echten‘ und ‚unechten‘ Objekten. ‚Unechte‘ Objekte wurden als ‚Eigenschaften‘ bezeichnet. Mit dieser Terminologie kann man sagen, dass die Objekthierarchie O primär von echten Objekten gebildet wird; unechte Objekte als Eigenschaften treten nur im Kontext eines echten Objekts auf. Damit kann man die begriffe ‚Gattung‘ und ‚Art‘ einführen. Gattungen, die keine Gattungen mehr ‚über sich‘ haben können, sollen hier ‚Kategorien‘ genannt werden. Setz man Definitionen von Worten voraus, dann kann man ach erklären, warum eine Aussage wie ‚a ist eine Tasse‘ ‚rein definitorisch‘ (bzw. ‚rein analytisch‘) ‚wahr ist, unabhängig davon, ob diesem gedanklichen Sachverhalt etwas Sinnliches entspricht. Im Gegensatz zu solch einer rein definitorischen (analytischen) Wahrheit eines Objekts a soll hier die ursprünglich vereinbarte ‚Wahrheit‘ durch Bezug auf eine ’sinnliche Gegebenheit‘ $latex s \subseteq Os$ ‚ontologische‘ Wahrheit genannt werden. Solange wir uns in unseren Aussagen auf das Enthaltensein eines Objektes a in einem Gattungsobjekts X beschränken ‚a ist ein X‘ oder das Feststellen von Eigenschaften der Art ‚a hat b‘ kann man sagen, dass eine Aussagestruktur wie (S P) wie folgt interpretiert werden kann: Es gibt einen Ausdruck A=(AsAp), bei dem ein Ausdrucksteil As sich auf ein echtes Objekt M(As) = $latex a \in Oa$ bezieht und der andere Ausdrucksteil Ap bezieht sich auf die Beziehung zwischen dem Objekt a und entweder einem Gattungsobjekt X (Ap = ‚ist ein X‘) oder auf eine Eigenschaft Y (Ap = ‚hat Y‘). Hierbei ist eine gewisse ‚Asymmetrie‘ zu beachten. Die Bedeutung vom Ausdrucksteil As – M(As) – bezieht sich auf eine ‚konkrete‘ Eigenschaftsstruktur innerhalb der Objekthierarchie. Die Bedeutung vom Ausdrucksteil Ap – M(Ap) – bezieht sich auf eine ‚Beziehung‘ / ‚Relation’/ ein ‚Verhältnis‘ [R] zwischen dem bezeichneten Bedeutungsobjekt M(As) = a und einem anderen bezeichneten Bedeutungsobjekt M(Ap), also R(M(As), M(Ap)). Die Beziehung R ist selbst kein ‚Objekt‘ so wie das Objekt a oder das implizit angenommene ‚Bezugsobjekt‘ X bzw. Y von a. Eine solche Beziehung R setzt – um prozessural ‚hantierbar‘ zu sein – eine zusätzliche ‚Objektebene‘ voraus, auf der es ein R-Objekt gibt, das die Beziehung zwischen dem a-Objekt und dem X-Y-Objekt ‚repräsentiert.

16. In dem Blogeintrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 16 wird die Analyse der vorausgesetzten Objekthierarchie O und der damit interagierenden Ausdrucksstruktur E weiter analysiert. Nach der Analyse der Feinstruktur von (S P) werden die Aspekte Anzahl, Raum und Zeit betrachtet. Es wird gezeigt, wie man für diese Aspekte sowohl ‚globale Quantoren‘ wie auch ‚lokale Relationen‘ einführen kann; zudem ist die Wechselwirkung zwischen diesen Aspekten konfliktfrei, da sie voneinander unabhängig sind.

17. In dem Blogeintrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 17 geht es um die Frage, wie man Aussagen über Veränderungen in der hypothetisch angenmmenen Bedeutungsstruktur nachzeichnen kann. Es lässt sich erkennen, dass die Kodierung von Veränderungen mittels Ausdruckselementen innerhalb eines Prädikates P mittels ‚Veränderungsausdrücken‘ V (‚Verben‘) oft nicht nur die beteiligten Objekte Y benennt, sondern zusätzlich zahlreiche weitere Ausdruckselemente aktiviert, die räumliche Gegebenheiten R_r bezeichnen, zeitliche Relationen R_t, zusätzliche Eigenschaften At an den Veränderungen; dazu ferner spezielle kulturelle Relationen R_x einbeziehen können sowie mit zusätzlichen Subjektrepräsentationen operieren. Auch kann man beobachten, wie die Aneinanderreihung von unterschiedlichen Sachverhalten (S P) mit logischen Operatoren (S P) UND (S2 P2) auch zu speziellen Verkürzungen führen kann wie (S P1 UND P2). Dies lässt erahnen, dass eine vollständige Analyse auch nur einer einzigen Alltagssprache von ihrer logisch relevanten Semantik her eine schier unendliche Aufgabe ist. Diese wird weder ein einzelner Mensch alleine noch viele Menschen über viele Genrationen hinweg jemals vollständig erfüllen können. Was aber möglich erscheint, das ist die Analyse des grundlegenden Mechanismus, der sich mit Hilfe von evolvierenden Computermodellen experimentell untersuchen und mit realen semiotischen Systemen überprüfen lässt.

18. In dem Blogeintrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 18 weitet sich nun der Blick Avicennas auf das Wissen allgemein, und konzentriert sich im Wissen auf das schlussfolgernde Denken in Form von ‚beweisenden Syllogismen‘. Nach einer Definition von ‚Syllogismus‘ unterscheidet er dann zwei Arten von Syllogismen ‚Konjunktiver‘ Syllogismen und ‚Disjunktiver‘ Syllogismus. Am Beispiel des ‚Konjunktiven Syllogismus‘ führt Avicenna dann eine Reihe von technischen Begriffen ein. Dann stellt Avicenna zusätzliche Beschränkungen vor, um die 256 möglichen Figuren/ Muster auf nur 27 mögliche Muster einzuschränken. Alle seine Festlegungen geschehen ohne eigentliche Begründung.

19. In dem Blogeintrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 19 beginnt die Diskussion um die Interpretation der syllogistischen Schlussfiguren am Beispiel der ersten Figur (A F B), (A B H) und (A F H) mit der Quantorenbelegung ‚AAA‘. In einzelnen Schritten wird dann eine erste Skizze zu einer Logik auf der Basis einer dynamischen Objektstruktur erarbeitet. Zentrale Begriffe sind hier OBJEKTIFIZIERUNG, ENTHALTENSEIN, ZUSCHREIBUNG und VERERBUNG. In dieser Skizze werden auch ‚Aktivitäten‘ berücksichtigt, die in dem Muster zur ersten Figur nicht vorkommen, zusätzlich werden neben den Anzahlquantoren auch Raum- und Zeitquantoren berücksichtigt.

20. In dem Blogeintrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 20 geht es um die Interpretation des zweiten Musters der ersten syllogistischen Schlussfigur ‚A F ist B‘, ‚A B ist nicht H‘ (als ‚Kein A ist B‘), ‚A F ist nicht H‘ (als ‚Kein F ist H‘), dazu die Beispiele ‚Jeder ausgedehnte Körper ist farbig‘, ‚Kein farbiger Körper ist unerschaffen‘, ‚Kein ausgedehnter Körper ist unerschaffen‘. Wir treffen in diesem Muster wieder auf den Prozess der Objektifizierung, tatsächlich sogar in impliziten Formen mit der expliziten Angabe von Eigenschaften und der stillschweigenden Annahme einer daraus sich ergebenden Mengenbildung. Zusätzlich finden sich wieder Enthaltensbeziehungen einerseits anhand von Eigenschaftszuschreibungen, andererseits durch Benutzung von Anzahlquantoren. Die Zuschreibung von Eigenschaften wird explizit vorgenommen. Eine Vererbung von Eigenschaften von einer Menge zur anderen tritt nur implizit über eine Enthaltensbeziehung auf. Es tritt nur eine Sorte von Quantoren auf. Auch sei angemerkt, dass außer der Negation kein weiterer aussagenlogischer Operator auftritt.

21. In dem Blogeintrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 21 geht es um die Interpretation der Muster 3-4 der Schlussfigur 1. Dabei entsteht die Vermutung, dass viele der Unterscheidungen von Avicenna (die weitgehend auf Aristoteles zurückgehen!) möglicherweise ‚redundant‘ sind, d.h. mit anderen Formulierungen letztlich doch ‚das Gleiche‘ sagen. Der Ansatzpunkt für diese Vermutung liegt darin begründet, dass die Unterscheidung von einem Term als ‚Subjekt‘ (S) und als ‚Prädikat‘ (P) auf Seiten der abstrakten Bedeutungsstruktur als Bedeutungsrepräsentation jeweils ein ‚echtes‘ oder ein ‚unechtes‘ Objekt haben können, und zwar so, dass diese Strukturen ‚fließend‘ sind: jedes ‚echte‘ Objekt kann als ‚unechtes‘ interpretiert werden und umgekehrt. Weitere Vereinfachungen deuten sich an. Diese sollen im Folgenden überprüft werden.

Fortsetzung folgt …

QUELLEN

  • Avicenna, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
  • Digital Averroes Research Environment
  • Immanuel Kant, Critik der reinen Vernunft‘, Riga, 1781
  • Konrad Lorenz, 1973, ‚Die Rückseite des Spiegels. Versuch einer Naturgeschichte des menschlichen Erkennens‘, München, Zürich: Piper
  • Günther Patzig, ‚Die Aristotelische Syllogistik‘, 3,verb.Aufl., Göttingen: Vandenhoeck & Rupprecht, 1969
  • Nicholas Rescher (1928 – ),The Development of Arabic Logic. University of Pittsburgh Press, 1964
  • Hans-Jörg Sandkühler (Hg.) unter Mitwirkung von Dagmar Borchers, Arnim Regenbogen, Volker Schürmann und Pirmin Stekeler-Weithofer, ‚Enzyklopädie Philosophie‘, 3 Bd., Hamburg: FELIX MEINER VERLAG, 2010 (mit CD-ROM)
  • Stanford Encyclopedia of Philosophy, Aristotle’s Logic
  • Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7

Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER.

AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 9

Affirmativ, Ausdruck, Ausdruck - einfacher, Ausdruck - sprachlicher, Ausdruck - zusammengesetzter, Aussage, Aussagetypen, Avicenna, Kategorisch, kontingent, Logik, Logik - Alltag, Logik - Antike, Logik - formale, Möglichkeit, Negation, Notwendig, Partikulär, Prädikat, Quantität, Quantor, Subjekt, universal, universell

(Mit Nachtrag vom 1.Sept.2014)

VORGESCHICHTE

Für einen Überblick zu allen vorausgehenden Beiträgen dieser rekonstruierenden Lektüre von Avicennas Beitrag zur Logik siehe AVICENNAS ABHANDLUNG ZUR LOGIK – BLITZÜBERSICHT.

Nach der üblichen Darstellung der Position von Avicenna folgt dann der Teil ‚DISKUSSION‘, in der seine Position kritisch hinterfragt und die Rekonstruktion einer möglichen Theorie der Alltagslogik fortgesetzt wird.

KATEGORISCH – AFFIRMATIV/ NEGATION – UNIVERSAL/ PARTIKULÄR

1. Im folgenden Abschnitt treten Begriffe auf, die z.T. schon zuvor auftraten (‚Kategorisch‘, ‚Negation‘, ‚Universal‘, ‚Partikulär‘), die aber jetzt mit neuen Randbedingungen nochmals diskutiert werden.

KATEGORISCH ALS AFFIRMATIV/ NEGATIV

2. Der Abschnitt beginnt mit einer Diskussion von ‚kategorischen‘ (‚kategorisierenden‘) Aussagen und der Frage, wann sie ‚affirmativ‘ und wann sie ’negativ‘ sind.

SUBJEKT – PRÄDIKAT, EINFACH – ZUSAMMENGESETZT

3. Zusätzlich zu den Unterscheidungen ‚affirmativ‘ – ’negativ‘ im Kontext einer ‚kategorisierenden‘ Aussage berücksichtigt Avicenna auch hier wieder Teilausdrücke. Während er zuvor die semantisch motivierten Begriffe ‚Name‘, ‚Verb‘ (auch ‚Term‘ genannt), sowie ‚Präposition‘ erwähnt hatte, benutzt er nun auch das Begriffspaar ‚Subjekt‘ und ‚Prädikat‘. Beide sind – wie sich aus dem Verwendungskontext nahelegt – ’semantisch‘ motiviert, d.h. nur durch Rückgriff auf die Bedeutung kann man zur Klassifikation ‚Subjekt‘ bzw. ‚Prädikat‘ kommen.
4. Versucht man die Begriffe ‚Name‘, ‚Verb‘ (‚Term‘), sowie ‚Präposition‘ mit den neuen Begriffen ‚Subjekt‘ und ‚Prädikat‘ in Beziehung zu setzen, dann gibt es eine gewisse Korrelation zwischen ‚Name‘ und ‚Subjekt‘ einerseits sowie ‚Verb‘ und ‚Prädikat‘ andererseits. Da Avicenna selbst keinerlei weitere Hinweise auf eine mögliche Beziehung liefert, bleibt an dieser Stelle einiges unklar.
5. Deutlich ist nur, dass Avicenna die Ausdrucksseite eines Ausdrucks e = <e1, e2, …> durch Rückgriff auf eine – nicht explizit beschriebene – Bedeutungsstruktur so analysiert, dass er sagen kann, welche ‚Teile‘ des Ausdrucks e als ‚Subjekt‘ zu nehmen sind, und welche Teile als ‚Prädikat‘.
6. So unterscheidet er im Bedeutungsraum zwischen ‚dem, über das‘ eine Feststellung getroffen wird, und ‚dem, was‘ in dieser Feststellung gesagt wird.
7. Im Beispielsatz N:(der Mensch)V:(ist)N:(ein Lebewesen) analysiert er den Teil [N:(der Mensch)] als ‚Subjekt‘ und den Teil [V:(ist)N:(ein Lebewesen)] als ‚Prädikat‘.
8. Ein anderer Beispielsatz (Wer immer)(sein)N:(Essen)OP:(nicht)V:(kaut)(der)V:(schädigt)(seinen)N:(Darm) enthält Aussageteile, für die Avicenna bislang keine semantisch motivierte grammatische Beschreibungskategorien eingeführt hat. Avicenna analysiert den Ausdruck wie folgt: Subjekt = [(Wer immer)(sein)N:(Essen)OP:(nicht)V:(kaut)] und Prädikat = [(der)V:(schädigt)(seinen)N:(Darm)].
9. Den Unterschied zwischen Subjekt = [N:(der Mensch)] und Subjekt = [(Wer immer)(sein)N:(Essen)OP:(nicht)V:(kaut)] charakterisiert Avicenna als Unterschied zwischen einem ‚einfachen‘ und einem ‚zusammengesetzten‘ Subjekt. Entsprechend auch für das Prädikat: Prädikat = [V:(ist)N:(ein Lebewesen)] und Prädikat = [(der)V:(schädigt)(seinen)N:(Darm)].
10. Sowohl für die Verwendung der Begriffe ‚Subjekt/ Prädikat‘ wie auch ‚einfach/ zusammengesetzt‘ liefert Avicenna keine explizite Kriterien. Er zitiert nur einige Ausdrücke als Beispiele und appelliert an die sprachliche Intuition des Lesers, die implizit verwendeten Analysekriterien zu verstehen.

AFFIRMATIV – NEGATIV

11. In den soeben erwähnten Kontexten wie auch in nachfolgenden Beispielen diskutiert er auch die Begriffe ‚affirmativ‘ und ’negativ‘.
12. Sein Hauptkriterium zur Verwendung der Begriffe ‚affirmativ‘ und ’negativ‘ ist der (semantische, bedeutungsgeleitete!) Aspekt, ob das, was in einer Aussage in einem Prädikat von einem Subjekt behauptet wird, ‚zutrifft’/ ‚der Fall ist‘ oder ’nicht zutrifft’/ ’nicht der Fall ist‘. Trifft das im Prädikat behauptete zu, dann will er es ‚affirmativ‘ nennen, ansonsten ’negativ‘.
13. Im vorausgehenden Abschnitt waren diese Verwendungskriterien auch benutzt worden, um zu sagen, wann eine Aussage ‚wahr‘ bzw. ‚falsch‘ ist. Nach den bisherigen Kriterien müsste man dann sagen, dass ‚wahr‘ und ‚affirmativ‘ einerseits und ‚falsch‘ und ’negativ‘ dann bedeutungsgleich wären.
14. In einem weiteren Beispiel benutzt Avicenna die Aussage SUBJ[N:(Zid)] PRÄD[V:(ist)(ohne)N:(Sicht)] – engl.: ‚Zid is without sight‘ – als ein Beispiel für eine ‚affirmative‘ Aussage, da das Prädikat PRÄD[V:(ist)(ohne)N:(Sicht)] eine Eigenschaft beschreibt, die auf das Subjekt (Zid) zutrifft.
15. Andererseits wird der Teilausdruck ‚ist ohne Sicht‘ bedeutungsmäßig als eine ‚Negation‘ verstanden im Sinne von ‚hat keine Sicht‘ im Gegensatz zu ‚hat Sicht‘. D.h. eine bedeutungsmäßige ‚Verneinung‘ kann durch verschiedene Ausdruckselemente realisiert werden, auch ohne den Ausdruck ’nicht‘. Dies würde bedeuten, dass eine ‚ausdrucksmäßig realisierte Verneinung‘ das Fehlen einer bestimmten Eigenschaft aussagen kann. Nach den Worten Avicennas kann aber genau solche eine Feststellung, dass eine bestimmte Eigenschaft fehlt, eine ‚Affirmation‘ sein, eben das Festellen, dass es der Fall ist, dass eine bestimmte Eigenschaft fehlt.
16. Wenn also eine Affirmation das Absprechen einer Eigenschaft beinhalten kann, wie sieht dann eine Verneinung einer solchen Affirmation aus?
17. Avicenna bringt folgendes Beispiel: SUBJ[N:(Zid)] PRÄD[V:(ist)(nicht)(ohne)N:(Sicht)]. Für ihn ist dieses eine ‚Negation‘, da die Affirmation, eine bestimmte Eigenschaft sei nicht da, verneint wird.
18. Mann könnte das Beispiel auch umschreiben zu: (Es ist nicht der Fall, dass) SUBJ[N:(Zid)] PRÄD[V:(ist)(ohne)N:(Sicht)].
19. Ersetzt man die Teilausdrücke durch Buchstaben – was Avicenna im Text auch einmal demonstriert –, dann könnte man auch schreiben (Es ist nicht der Fall, dass) (A)(B), bzw. dann $latex (A)\neg(B)$.

EXISTENZ

20. Zwischendrin bemerkt Avicenna auch mal, dass das Treffen einer Feststellung, eigentlich nur Sinn mache, wenn dasjenige, von dem etwas ausgesagt wird, auch existiere. Doch wird dieser Punkt nicht weiter diskutiert.

UNIVERSELL – PARTIKULÄR – QUANTITÄT – QUANTOREN

21. Vom Subjekt einer Aussage sagt Avicenna, sie kann ‚partikulär‘ oder ‚universell‘ sein. Falls universell, dann kann man unterscheiden, ob sie ‚unbestimmt‘ (engl.: ‚indeterminate‘) ist – wie viele genau involviert sind — oder eben ‚bestimmt‘ (engl.: ‚determinate‘).
22. Im Beispielausdruck (Zid)(ist)(ein)(Lebewesen) ist (Zid) ‚partikulär‘.
23. Im Beispielausdruck (Menschen)(bewegen)(sich) ist nach Avicenna unklar, ob ‚alle‘ Menschen gemeint sind oder nur ‚einige‘.
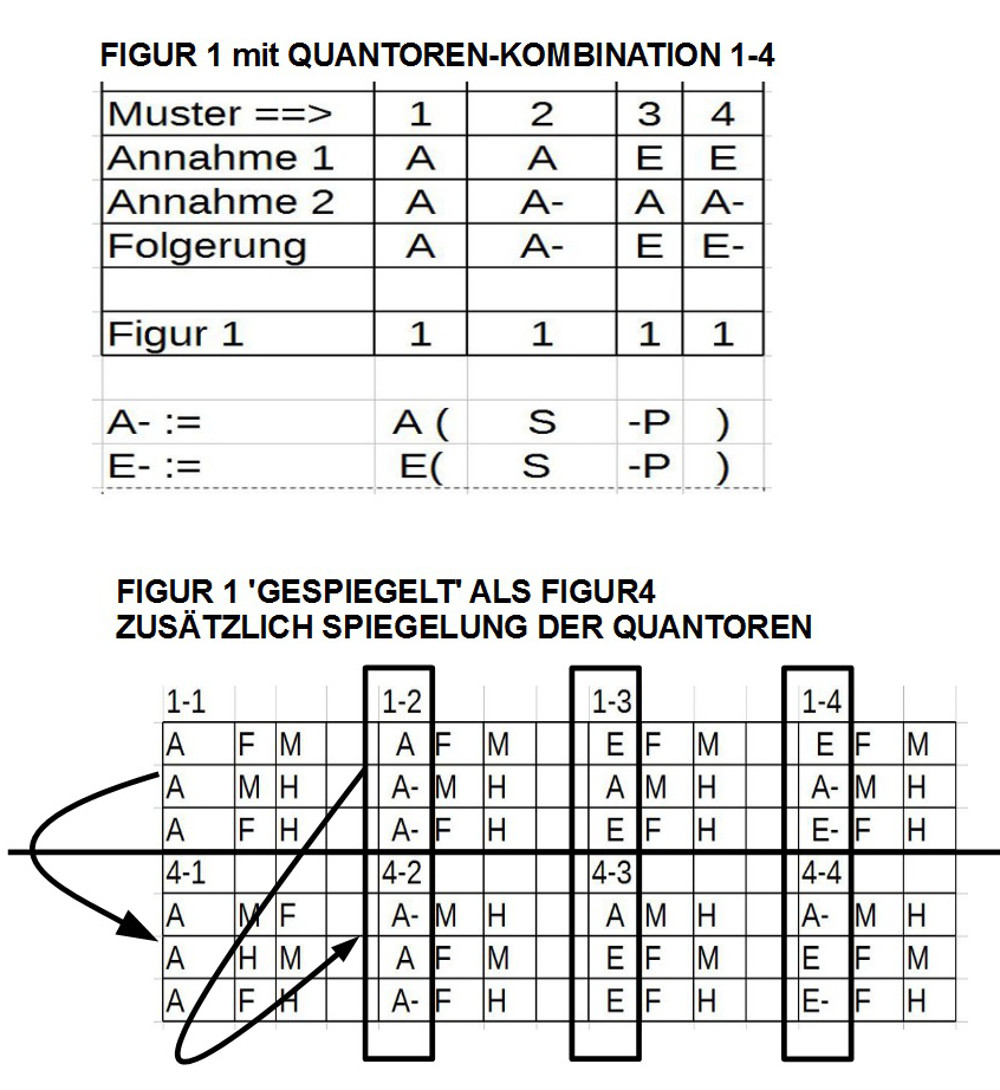
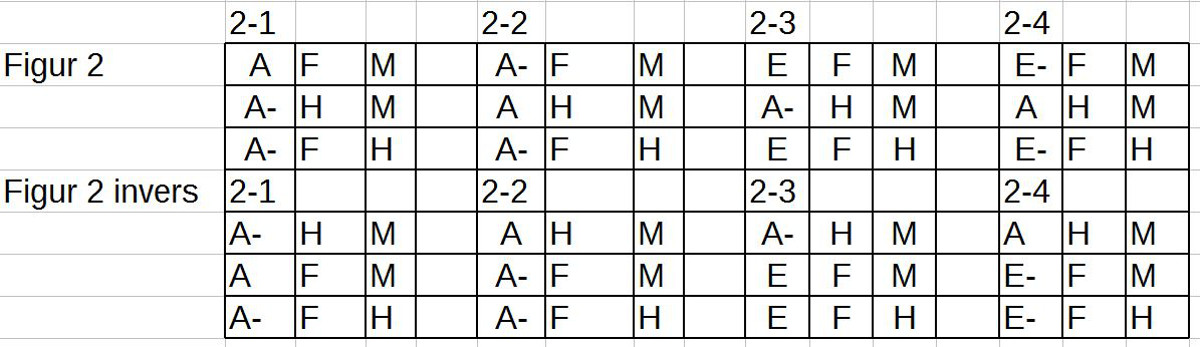
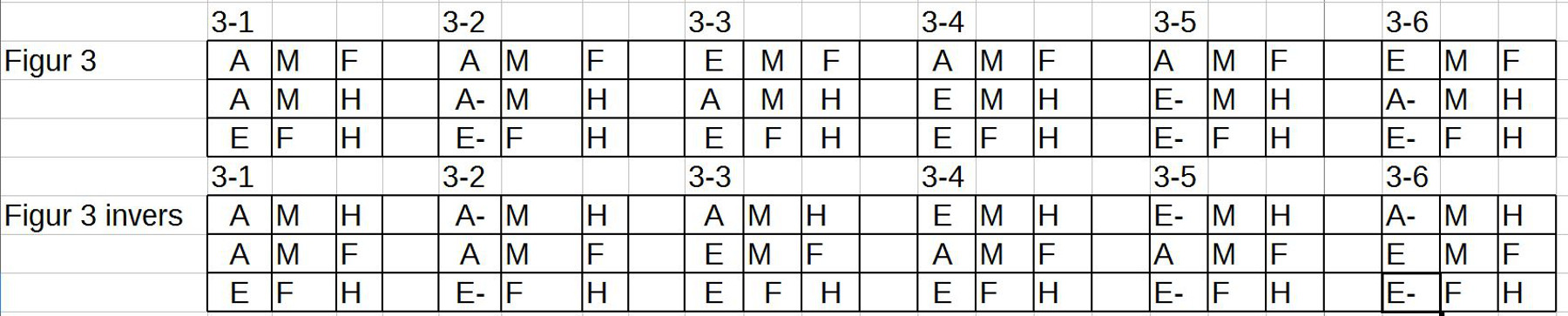
24. Die ‚bestimmten universellen Aussagen‘ teilt Avicenna in vier Klassen ein:
25. Typ 1: Subjekt = Alle, Affirmativ (Bsp.: Q=[(Jeder)]S=[(Mensch)]P=[(ist)(ein)(Lebewesen)]
26. Typ 2: Subjekt = Alle, Negativ (Bsp.: Q=[(Kein)]S=[(Mensch)]P=[(ist)(sterblich)](?)
27. Typ 3: Subjekt = Einige, Affirmativ Q=[(Einige)]S=[(Mensch)]P=[(sind)(Schriftsteller)]
28. Typ 4: Subjekt = Einige, Negativ Q=[(Nicht alle)]S=[(Mensch)]P=[(sind)(Schriftsteller)] (?)
29. Hier sind nur einige von Avicennas Beispielsätzen angeführt. Einige Beispiele werfen Fragen auf (?).
30. Mehrfach formuliert Avicenna auch folgendes ‚Metaprinzip‘: Wenn eine Aussage über ‚Alle‘ spricht, dann sei es unsicher, ob wirklich alle gemeint sind; sicher sei es aber, dass wenigstens ‚einige‘ gemeint sind.
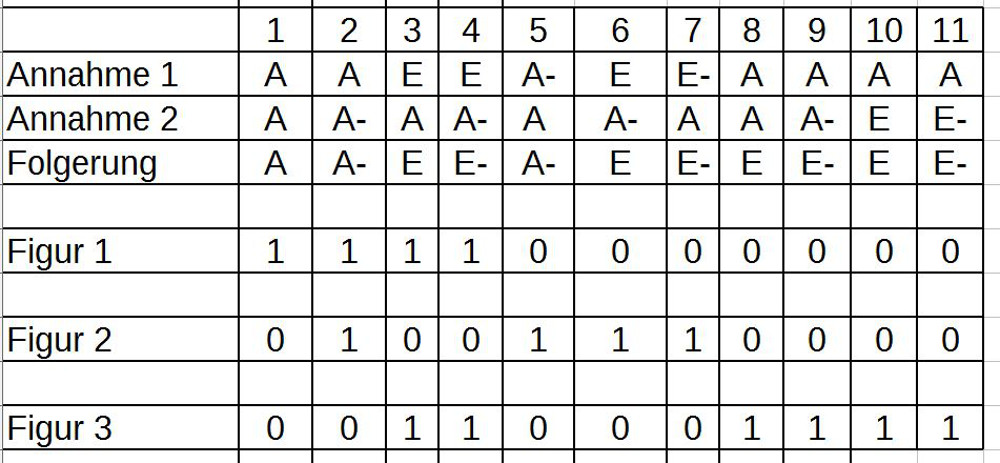
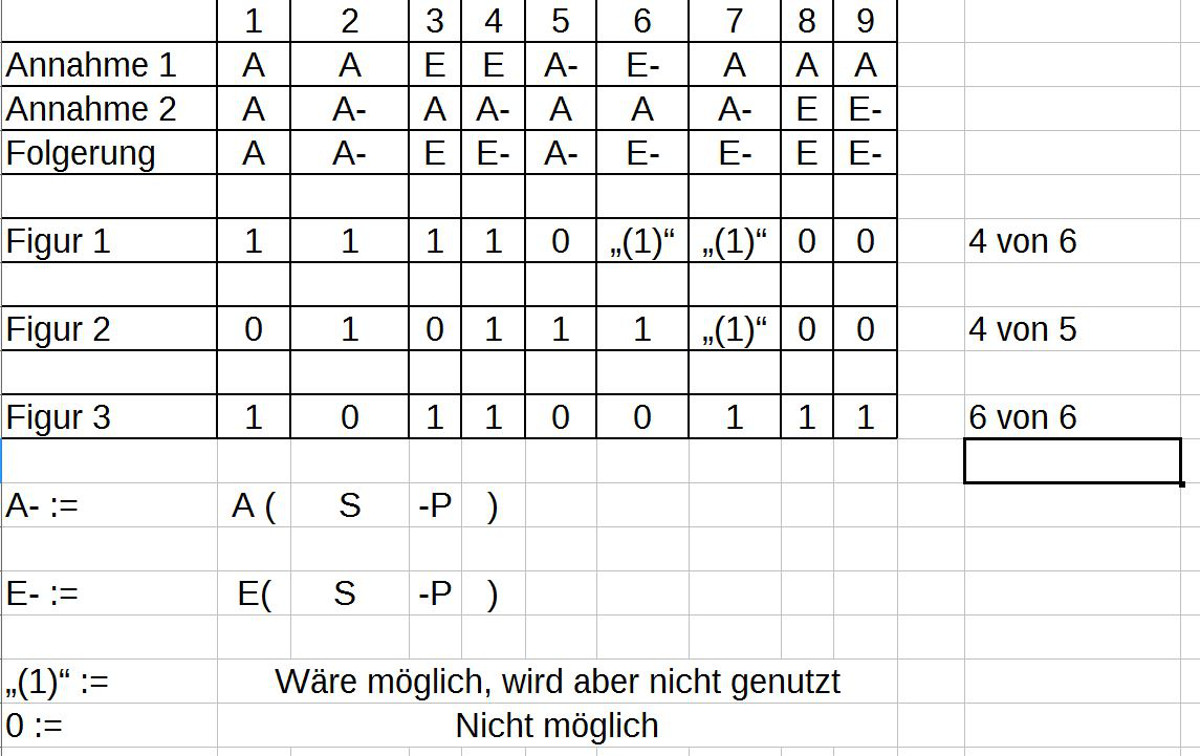
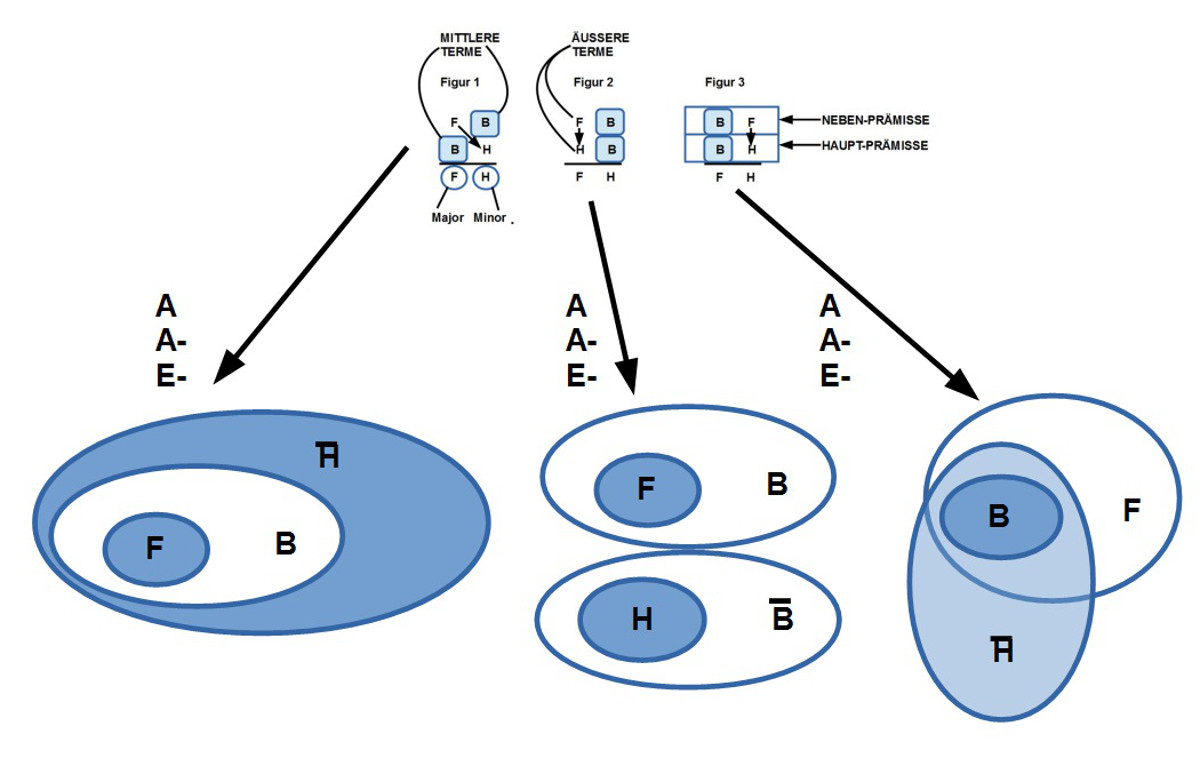
31. Aus all diesen Überlegungen leitet er dann folgende Fallunterscheidungen her (von mir abgekürzt ‚+‘ für ‚affirmativ‘, ‚-‚ für negativ‘, ‚1‘ für ‚partikulär‘, ‚0‘ für ‚unbestimmt‘ und ‚a‘ für universell‘:
32. (+,1)
33. (-,1)
34. (0,+)
35. (0,-)
36. (a,+)
37. (a,-)
38. (1,+)
39. (1,-)
40. Die Fälle (+,1) und (-,1) bezeichnet Avicenna als ’nutzlos für die Wissenschaft‘ und die Fälle (0,+) und (0,-) sollten vermieden werden, da sie ‚verwirrend‘ sind.

NOTWENDIG – KONTINGENT

41. Am Beispiel der kategorisierenden Aussagen illustriert Avicenna auch die Begriffe ’notwendig‘ und ‚kontingent‘. Die Verwendung dieser Begriffe stimmt überein mit den zuvor eingeführten Begriffe ‚wesentlich‘ und ‚akzidentell‘.

MÖGLICH

42. Auch erwähnt Avicenna hier den Begriff ‚möglich‘. Er sieht mindestens zwei Verwendungsweisen von ‚möglich‘: einmal als (i) ’nicht unmöglich‘ und (ii) im Sinne von ‚kann existieren‘ und ‚kann nicht existieren‘. Fall (ii) ist für ihn das ‚real mögliche‘ und stimmt nach Ihm mit dem normalsprachlichen Gebrauch überein.
43. Die Verwendungsweise in Fall (i) von ‚möglich := nicht unmöglich‘ widerspricht eigentlich den Regel einer expliziten Definition, wie er sie an früherer Stelle aufgestellt hatte. Dort hatte er verlangt, dass der neu zu definierende Ausdruck e_new nicht auf der rechten Seite bei den definierenden – als bekannt vorausgesetzten – Ausdrücken vorkommen darf, also e_neu := <e_alt1, …, e_altn>.
44. Der Ausdruck ‚möglich := nicht unmöglich‘ entspricht dem Ausdruck ‚möglich := nicht nicht möglich‘. Darin wird der neue Ausdruck über sich selbst definiert, was ‚zirkulär‘ ist.

DISKUSSION

45. Dieser neue Text verstärkt den Eindruck der vorausgehenden Seiten, dass Avicenna keine wirklich systematische Theorie hat. Er folgt den in der Literatur vorkommenden Begriffen nach keiner erkennbaren Regel, und seine Analyse benutzt Kriterien, die höchst selten explizit benannt werden. Vorzugsweise stellt er Beispielsätze vor, die er nach impliziten Kriterien diskutiert. Auch wiederholt er scheinbar ähnliche Bedeutungszusammenhänge mit jeweils neuen Begriffen. Dennoch besteht noch immer der Eindruck, dass sich der bislang gewählte Interpretationszusammenhang durchhalten lässt.

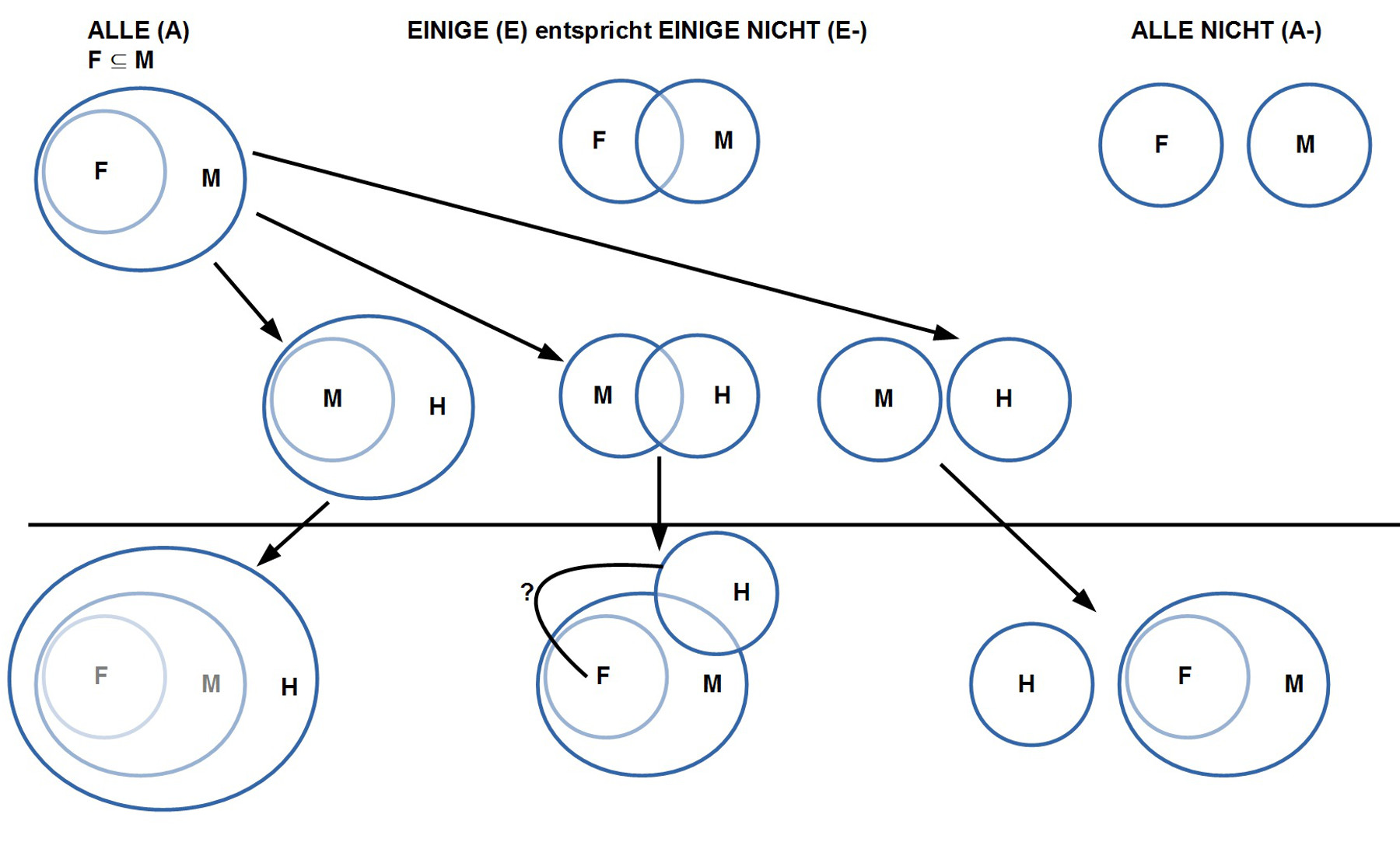
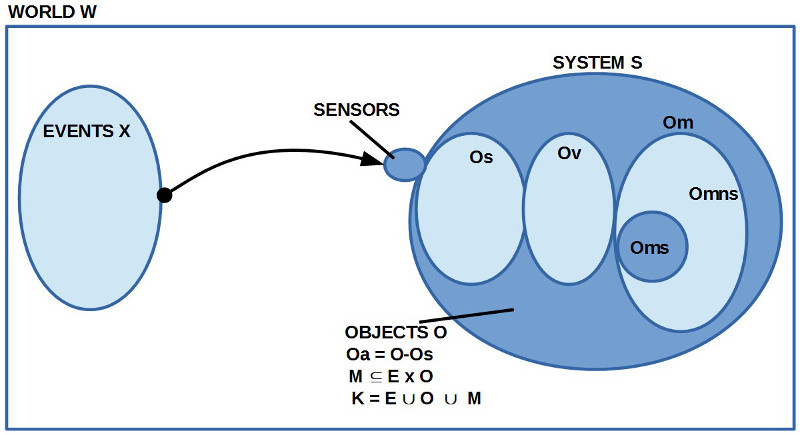
REKONSTRUIERENDE ECKWERTE BISHER

46. Als Eckwerte der rekonstruierenden Interpretation gilt bislang die Unterscheidung vom (i) ‚wissenden System‘ S in einer (ii) umgebenden realen Welt W und der Fähigkeit des wissenden Systems, (iii) bestimmte Ereignisse X der realen Welt W über einen Verarbeitungsprozess $latex \lambda$ in einen (iv) internen Bedeutungsraum M zu übersetzen. Parallel zum Bedeutungsraum M gibt es (v) eine Menge von Ausdrücken E, die (vi) auf unterschiedliche Weise mit dem Bedeutungsraum E innerhalb einer gewussten Beziehung $latex K \subseteq E \times M$ verknüpft werden können. Im Bereich des Bedeutungsraumes M kann (vii) unterschieden werden zwischen ‚aktuellen‘ Bedeutungsrepräsentationen M_now, die von aktuellen Ereignissen X der realen Welt verursacht sind, und ‚zeitlosen‘ Bedeutungsrepräsentationen M_0, mit $latex M_{now} \cap M_{0} = \emptyset, M_{now} \subseteq M, M_{0} \subseteq M$. Der Unterschied zwischen $latex M_{now}, M_{0}$ bezieht sich auf die zeitliche Komponente T in $latex M_{now}, M_{0}$. Würde man die zeitliche Komponente T aus $latex M_{now}$ ‚herausrechnen (also etwa $latex M_{now0} = M_{now} – T$), dann könnten die beiden Mengen $latex M_{now}, M_{0}$ gemeinsame Elemente enthalten ($latex M_{now0} \cap M_{0} \neq \emptyset$ ). Dies bedeutet, dass die charakterisierenden Eigenschaften der Objekte in $latex M_{now*}, M_{0}$ wissensmäßig ‚gleich‘ sein können. Durch (viii) Vergleich von Elementen aus M_now0 und M_0 kann dann entschieden werden, ob es der Fall ist, dass Elemente aus M_0 in M_now vorkommen oder nicht; falls sie vorkommen, dann ist eine feststellende (affirmative oder negative) Aussage ‚wahr‘, ansonsten ‚falsch‘.

REKONSTRUKTION: AFFIRMATIV – NEGATIV

47. Schon bei den von Avicenna angeführten Beispielen und deren Diskussion wird deutlich, dass eine gewisse Unklarheit darüber existiert, wie ’negative Ausdruckselemente‘ (wie z.B. ’nicht‘, ‚ohne‘) innerhalb des Begriffspaares ‚affirmativ/ negativ‘ zu bewerten sind. Zwar macht Avicenna darauf aufmerksam, dass das ‚Fehlen von etwas‘ eine Eigenschaft sein kann, die man ja gerade – affirmativ — aussagen möchte, aber es fehlt letztlich ein hartes Kriterium, wann das ‚Fehlen‘ von etwas nur ein ‚Ausdruckselement‘ ist oder ein ’semantischer Tatbestand‘, der ‚oberhalb‘ der Ausdruckselemente liegt, also wo es gerade das ‚Fehlen von etwas‘ ist, das man aussagen will.
48. In dieser Rekonstruktion wird davon ausgegangen, dass jede Aussage – entsprechend den Aussagen von Avicenna – entweder ‚wahr‘ oder ‚falsch‘ ist. Dies setzt voraus, dass jede Aussage als solche ‚grundsätzlich affirmativ‘ ist, sie will etwas über ein Subjekt aussagen. Für diese Aussage wird ein Ausdruck e generiert (in der Regel mit mehreren Teilausdrücken, mindestens Subjekt und Prädikat), der einen Sachverhalt m_p mittels des Prädikats über ein Subjekt m_s behauptet. Innerhalb der Aussage e kann der Sachverhalt m_p sowohl ‚zusprechend‘ (affirmativ) im Sinne von ‚ist ein…’/ ‚hat …‘ sein oder absprechend, negierend ‚ist nicht …‘, ‚hat nicht …‘ usw. Unabhängig davon ob die kombinierten Sachverhalte (m_s, m_p) ‚zusprechend‘ oder ‚absprechend‘ sind, können sie ‚wahr‘ (in der realen Welt W zutreffend) oder ‚falsch‘ (in der realen Welt W nicht zutreffend) sein.
49. Während die Frage von ‚wahr’/ ‚falsch‘ eine rein semantische Angelegenheit ist, die durch die simultane wissensmäßige Unterscheidung von ’nur gewusst/ gedacht/ vorgestellt/ erinnert/ im Sinne von $latex M_{0}$ einerseits und ‚als aktuell wahrgenommen gewusst‘ im Sinne von $latex M_{now}$ möglich ist, hängt die Unterscheidung von ‚affirmativ/ negativ‘ davon ab, ob es Ausdruckselemente gibt, die explizit so vereinbart sind, dass sie in einem S-P-Urteilszusammenhang als ‚zusprechend‘ oder ‚absprechend‘ identifiziert werden können. Wenn niemand weiß, dass ’nicht‘ in der Deutschen Sprache eine ‚Verneinung‘ darstellt, kann auch kein ‚Absprechen von etwas‘ erkennen. Wenn jemand aber weiß, dass mit dem Ausdruckselement ’nicht‘ etwas verneint wird, dann weiß er aufgrund der Aussagensemantik, dass der Ausdruck ‚ist nicht sterblich‘ eben die Verneinung von ‚ist sterblich‘ ist (unabhängig von ‚wahr‘ und ‚falsch‘). Und da die Bedeutung der Verneinung an den Ausdruck ’nicht‘ geknüpft ist, wird diese Bedeutung jedes mal aktiviert, wenn das Ausdruckselement ’nicht‘ auftritt: ‚ist nicht sterblich‘, ‚ist nicht nicht sterblich‘, ‚es gilt nicht, dass Zid nicht unsterblich ist‘, usw. Allerdings sind die Konventionen in jeder Sprache unterschiedlich, wie das Auftreten von negierenden Ausdruckselementen vorzunehmen ist (während im Deutschen eine Häufung wie ’nicht nicht‘ in Grenzfällen noch gehen mag, geht ’nicht nicht nicht‘ normalerweise nicht mehr. Darüber hinaus gibt es zahllose andere Ausdruckselemente (wie z.B. ‚kein(e), mit, ohne, haben, …), die auch negierende Funktionen übernehmen können.
50. Ein Ausdruck wie (Zid (ist ohne Sicht)), bedeutungsmäßig äquivalent etwa zu zu (Zid (hat keine Sicht)) oder (Zid (kann nicht sehen)), sagt affirmativ ein Fehlen aus. Ob dies während der Aussage in der realen Welt zutrifft (= wahr) oder nicht (=falsch), folgt aus der Aussage selbst nicht.
51. Eine Verneinung dieser Aussagen geschieht zunächst auf der Ausdrucksebene, und dann kann man den so konstruierten Sachverhalt bzgl. Wahrheit oder Falschheit bewerten.
52. Es hängt von geltenden Konventionen ab, wie man die Verneinung der Aussage (Zid (ist ohne Sicht)) auf der Ausdrucksebene realisiert. Eine Möglichkeit besteht darin, auf einer Metaebene zu sagen, ‚Die Aussage (Zid (ist ohne Sicht)) trifft nicht zu. Dies würde primär aber meinen, dass diese Aussage in der realen Welt W nicht zutrifft. Würde man die interne Struktur der Aussage (Zid (ist ohne Sicht)) ändern, dann würde man eine neue Aussage schaffen, von der man wiederum fragen kann, ob sie in der realen Welt W zutrifft oder nicht. Also man könnte natürlich formulieren (Zid (ist nicht ohne Sicht)); damit würde man verneinen, dass Zid ohne Sicht sei, also eine Verneinung der vorhergehenden Aussage. Aber auch diese neuerliche Verneinung wäre grundsätzlich eine Affirmation, nämlich etwas, was man über Zid Aussagen will.
53. Die rekonstruierende Hypothese lautet also: jeder Ausdruck e vom Typ Aussage PROP impliziert die Affirmation eines Sachverhaltes m_p über ein Subjekt m_s unabhängig davon, wie viele Negationen/ Verneinungen der Ausdruck e enthält. Eine so realisierte affirmative Aussage zu (m_s, m_p) kann wahr oder falsch sein.

EXISTENZ

54. Das von Avicenna nur kursorisch erwähnte Moment der Existenz ist in der aktuell rekonstruierenden Interpretation gegeben durch die Annahme der umgebenden realen Welt W, deren aktuelle induzierten Bedeutungsrepräsentationen M_now als Bezugspunkt für die Charakterisierungen wahr/ falsch genutzt werden kann. In diesem Rahmen können beliebige Aussagen gebildet werden ,unabhängig davon, ob sie aktuell wahr/ falsch sind.

MÖGLICH

55. Die Kategorie ‚möglich‘ ist durch die bloße Angabe ‚kann existieren und kann nicht existieren‘ kaum erklärt. Zu sagen, dass ein B über ein gegebenes/ bekanntes A ‚hinausgeht‘, setzt eigentlich voraus, dass man die Ereignisse X der realen Welt W zunächst mal überhaupt als ‚exstierend‘ erkennen kann $latex \lambda(X)$ , so dass dann relativ zu diesem Wissen $latex \lambda(X)$ ein anderes Element Y als ’neu‘ oder als ‚möglich‘ explizit gedacht werden könnte. Wir wissen vom menschlichen Denken, dass wir uns allerlei Dinge als M_0 ‚vorstellen‘, ‚denken‘, ‚träumen‘ … können, von denen zum Zeitpunkt des Vorstellens nicht bekannt ist, ob sie sich genauso auch ereignen werden. Bei einigen dieser Vorstellungen M_0* haben wir ein zusätzliches Wissen K*, aufgrund dessen wir aus der Vergangenheit wissen, dass sie mit einer gewissen Wahrscheinlichkeit eintreten können; von daher räumen wir diesen mittels K* als ‚eintretbar‘ klassifizierten Vorstellungen M_0* eine gewisse Möglichkeit ein. Bei anderen Vorstellungen $latex M_{X} = M_{0} – M_{0*}$ ist es uns weniger bis gar nicht klar, ob sie eintreten können, da das zugehörige Wissen K_X zu schwach ist.

QUNATITÄT – QUANTOREN

56. Im Kontext der schon zuvor erwähnten Begriffe ‚universell‘ und ‚partikulär‘ führt Avicenna nun den Gedanken der ‚Bestimmtheit’/ ‚Unbestimmtheit‘ ein und entwickelt daraus die Idee der Quantität in Gestalt von Quantoren.
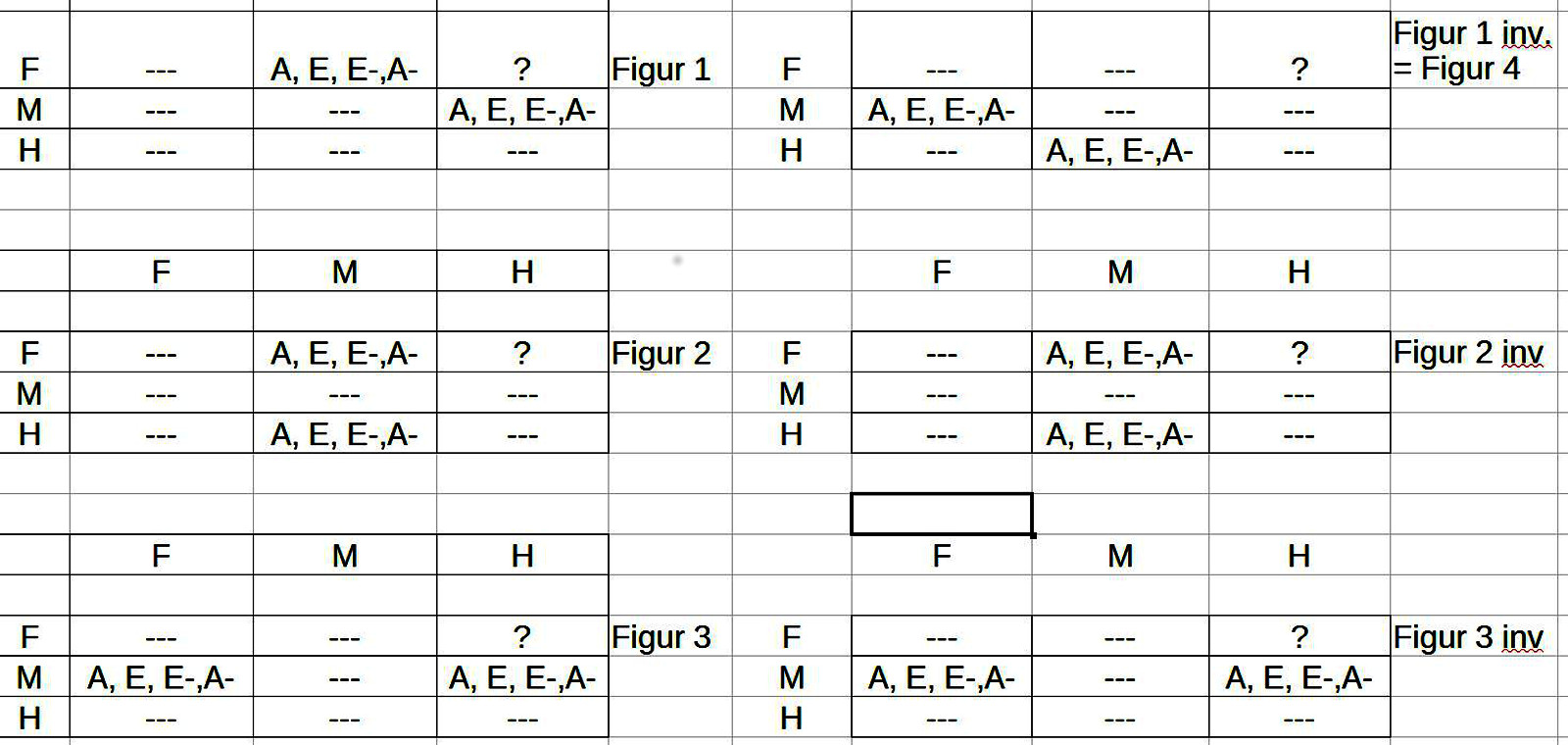
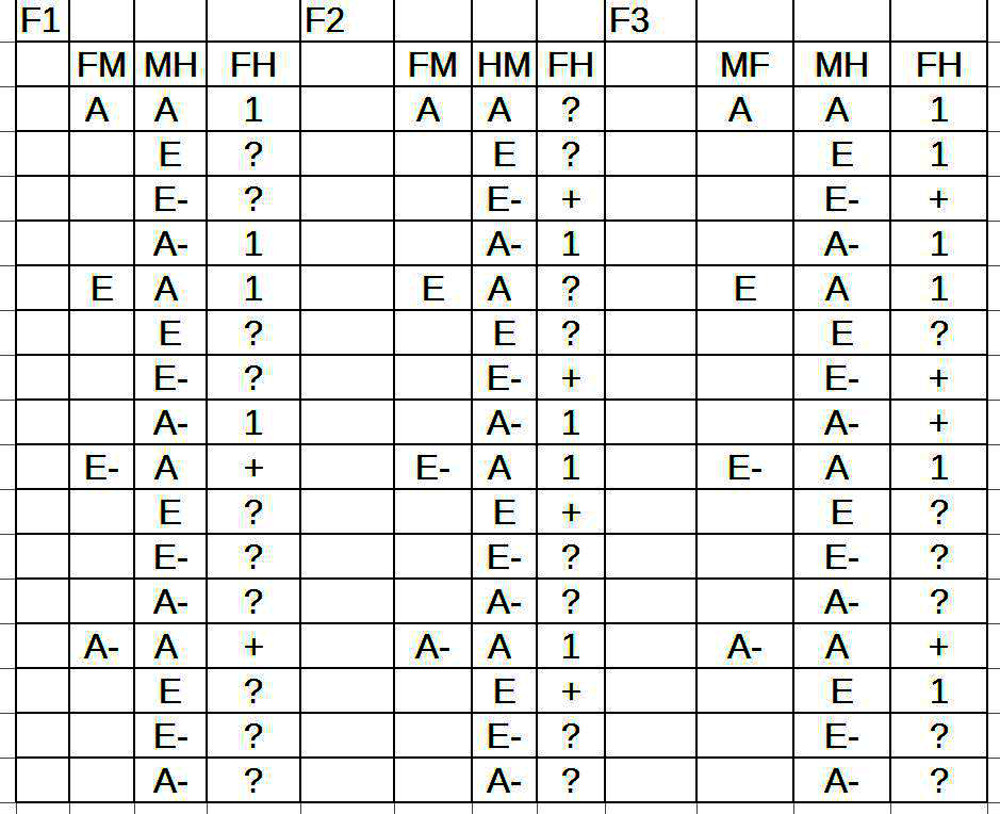
57. Dies führt zu der grundsätzlichen Erweiterung (Q,S,P), d.h. das Zutreffen eines Sachverhaltes m_p wird nicht mehr nur für ein Subjekt S allgemein behauptet, sondern das Objekt m_s, das bedeutungsmäßig ein Subjekt fundiert, wird bezüglich seiner Quantität Q weiter spezifiziert als ‚Alle/ Jeder‘, ‚Nicht Alle/Einige‘, ‚Alle – nicht/ Keine(r)‘.
58. Bei der konkreten Angabe der sich daraus ergebenden möglichen Klassen kommt es aber dann bei Avicenna zu Unklarheiten, da er bei dieser Einteilung sein Begriffspaar ‚affirmativ/ negativ‘ benutzt, von dem wir zuvor gesehen haben, dass es möglicherweise ‚fehlerhaft‘ ist, da er den Begriff ‚affirmativ‘ und ’negativ‘ auf die gleiche semantische Stufe stellt. Wie zuvor aber schon festgestellt worden ist, muss man diese beiden Begriffe trennen. Wenn Avicenna z.B. die beiden ersten Typen seiner Aussagen klassifiziert als
59. Typ 1: Subjekt = Alle, Affirmativ (Bsp.: Q=[(Jeder)]S=[(Mensch)]P=[(ist)(ein)(Lebewesen)] oder Q=[(Jeder)]S=[(Mensch)]P=[(ist)(sterblich)]
60. Typ 2: Subjekt = Alle, Negativ (Bsp.: Q=[(Kein)]S=[(Mensch)]P=[(ist)(sterblich)](?)
61. dann ist die Charakterisierung von Typ 1 nachvollziehbar, von Typ 2 aber nicht. Von der Idee her soll in Typ 2 gezeigt werden, wie die Negation von Typ 1 beschaffen ist. In Typ 1 wird (affirmativ) behauptet, dass jeder Mensch ein Lebewesen ist bzw. sterblich ist. Im Typ 2 soll auch etwas (affirmativ) behauptet werden, nämlich dass ’nicht alle‘ Menschen Lebewesen sind bzw. sterblich sind. D.h. die Aussagen vom Typ 2 sind grundsätzlich weiterhin ‚affirmativ‘, es wird aber in ihrem Ausdruck ein zusätzliches verneinendes Ausdruckselement – hier ’nicht‘ – eingeführt, so dass der Sachverhalt, der affirmativ behauptet werden soll, ein zusätzliches verneinendes Element enthält. Daraus würde sich ergeben:
62. Typ 2b Q=[(Nicht alle)]S=[(Menschen)]P=[(sind)(sterblich)], was man umformen könnte zu Q=[(Einige)]S=[(Menschen)]P=[(sind)(nicht)(sterblich)].
63. Aus (nicht alle) folgt nicht (keine), wie bei Avicenna, sondern (einige).
64. Auch im Beispiel der Verneinung von ‚einige‘ kommt es bei Avicenna zu Unklarheiten:
65. Typ 3: Subjekt = Einige, Affirmativ Q=[(Einige)]S=[(Mensch)]P=[(sind)(Schriftsteller)]
66. Typ 4: Subjekt = Einige, Negativ Q=[(Nicht alle)]S=[(Mensch)]P=[(sind)(Schriftsteller)] (?)
67. Im Fall von Typ 4 geht es um die (affirmative) Behauptung, dass ’nicht einige‘ gemeint sind. Aus ’nicht einige‘ folgt aber nicht – wie bei Avicenna – ’nicht alle‘, sondern ‚(alle …. nicht…), d.h.
68. Typ 4b: Q=[(Nicht einige)]S=[(Mensch)]P=[(sind)(Schriftsteller)] kann umgeformt werden zu Q=[(Alle)]S=[(Mensch)]P=[(sind)(nicht)(Schriftsteller)]
69. Daraus folgt, dass eine Klassifikation nicht nach dem Muster (Q -affirmativ) und (Q – negativ) vorgenommen werden sollte, sondern nach dem Muster, alle Aussagen sind ‚affirmativ‘; innerhalb dieser Menge kann man verschiedene Quantoren unterscheiden (alle) bzw. (einige), und diese Quantoren sind entweder nicht verneint oder verneint. Das würde folgendes Schema ergeben:
70. Typ 1: Q=’alle‘
71. Typ 2b: Q='(nicht)(alle)‘ bzw. $latex (\neg)(Q)$ ist äquivalent zu Q=(einige),S,($latex \neg$),P).
72. Typ 3: Q=’einige‘
73. Typ 4b: Q='(nicht)(einige)‘ bzw. $latex (\neg)(Q)$ ist äquivalent zu Q=(alle),S,($latex \neg$),P).
74. Das von Avicenna formulierte ‚Metaprinzip‘: ‚Wenn eine Aussage über ‚Alle‘ spricht, dann ist es unsicher, ob wirklich alle gemeint sind; sicher ist es aber, dass wenigstens ‚einige‘ gemeint sind‘, muss auch hinterfragt werden. Würde sein Metaprinzip gelten, dann könnte man keine wirklichen ‚All-Aussagen‘ mehr machen, da grundsätzlich die intendierte Bedeutung von ‚alle‘ verneint würde. Dies macht keinen Sinn. Wenn jemand tatsächlich ‚alle‘ meint und dies ausdrücken will, dann muss der dazu vereinbarte Ausdruck ‚alle‘ auch entsprechend verwendet werden.
75. Die von Avicenna vorgenommene Fallunterscheidungen (von mir abgekürzt ‚+‘ für ‚affirmativ‘, ‚-‚ für negativ‘, ‚1‘ für ‚partikulär‘, ‚0‘ für ‚unbestimmt‘ und ‚a‘ für universell‘) der Art:
76. (+,1)
77. (-,1)
78. (0,+)
79. (0,-)
80. (a,+)
81. (a,-)
82. (1,+)
83. (1,-)
84. leidet an der gleichen Schwäche, wie schon zuvor bei der Diskussion seiner vier Quantorentypen, hier verstärkt um sein falsches Metaprinzip. Klammert man ‚affirmativ‘ als Einteilungskriterium aus, da dies auf alle Typen zutrifft, bleiben nur die beiden Quantoren und deren Verneinung:
85. Q=’alle‘,S,P
86. Q=(nicht)(alle),S,P $latex \leftrightarrow $ Q=(einige),S,(nicht),P
87. Q=’einige‘,S,P
88. Q=(nicht)(einige),S,P $latex \leftrightarrow $ Q=(alle),S,(nicht),P
89. Wollte man den umgangssprachlichen Quantor ‚keiner‘ benutzen, könnte man diesen über Typ 4b definieren: Q=’kein(er)‘,S,P $latex \leftrightarrow$ Q=(alle),S,($latex \neg$),P).

Fortsetzung folgt …

QUELLEN

  • Avicenna, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
  • Digital Averroes Research Environment
  • Stanford Encyclopedia of Philosophy, Aristotle’s Logic
  • Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7

Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER.

AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 8

Aussage, Aussagetypen, Avicenna, Disjunktion, Falsch, Knjunktion, Konjunktion, Logik, Logik - Alltag, Logik - Antike, Logik - formale, Negation, Operator, Operator - aussagenlogischer, Wahr, Wahrheit als Übereinstimmung, Wahrheitsbegriff, Wahrheitswert

VORGESCHICHTE

1. In einem ersten Beitrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 1 hatte ich geschildert, wie ich zur Lektüre des Textes von Avicenna gekommen bin und wie der Text grob einzuordnen ist. In einem zweiten Beitrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 2 ging es um die Frage, warum überhaupt Logik? Avicenna führt erste Unterscheidungen zu verschiedenen Wissensformen ein, lässt aber alle Detailfragen noch weitgehend im Dunkeln. Im Teil AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 3 ging es um einfache und zusammengesetzte Begriffe, und bei den einfachen Begriffen um ‚individuelle‘ und ‚universelle‘. Schon hier zeigt sich der fundamentale Unterschied zwischen der antiken und der modernen-formalen Logik. In der antiken Logik wird die Ausdrucksebene E – und einer sich daran manifestierenden Folgerungslogik – immer in Verbindung mit einer zugehörigen Bedeutungsstruktur gesehen, die sich an einer Objektstruktur O festmacht. Die moderne formale Logik kennt zwar auch ‚Semantiken‘ und ‚Ontologien‘, diese sind aber ’sekundär‘, d.h. es werden nur solche ‚formalen Semantiken‘ betrachtet, die zum vorausgesetzten syntaktischen Folgerungsbegriff ‚passen‘. Dies sollte dann später an konkreten Beispielen diskutiert werden. Hier liegt der Fokus auf der antiken Logik im Sinne Avicennas. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 4 knüpft Avicenna an den zuvor eingeführten Begriff des ‚universellen‘ Begriffs an und betrachtet jetzt solche als ‚universell‘ bezeichneten Ausdrücke in einem Ausdruckskontext von aufeinanderfolgenden Ausdrücken. Alle diese Ausdrücke könnte man im Sinne der antiken Logik auch als ‚Urteile‘ bezeichnen, durch die einem bestimmten Ausdruck durch andere Ausdrücke bestimmte Bedeutungen (Eigenschaften) zu- oder abgesprochen werden. Hier unterscheidet er die Fälle eines ‚wesentlichen‘ Zusammenhanges zwischen zwei Begriffen und eines ’nicht wesentlichen‘ – sprich ‚akzidentellen‘ – Zusammenhangs. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 5 führt Avicenna eine Reihe von neuen technischen Begriffen ein, die sich nicht alle in ihrer Bedeutung widerspruchsfrei auflösen lassen. Es handelt sich um die Begriffe ‚Genus‘, ‚Spezies‘, Differenz, allgemeine und spezielle Akzidens, den Begriff ‚Kategorie(n)‘ mit den Kategorien ‚Substanz‘, ‚Qualität‘ und ‚Quantität‘. Die Rekonstruktion führt dennoch zu spannenden Themen, z.B. zu einem möglichen Einstieg in das weltverändernde Phänomen der kognitiven Evolution. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 6 geht es um die Begriffe ‚Definition‘ und ‚Beschreibung‘. Im Verhältnis zwischen beiden Begriffen geht die Beschreibung der Definition voraus. In der ‚Definition‘, die Avicenna vorstellt, wird ein neuer Ausdruck e mittels anderer Ausdrücke <e1, …, ek>, die sich auf schon bekannte Sachverhalte beziehen, ‚erklärt‘. Die von Avicenna dann vorgenommene Erklärung, was eine ‚Definition‘ sei, hängt u.a. stark ab von dem Begriff der ‚Bekanntheit‘ und dem Begriff des ‚wahren Wesens‘. Für die Tatsache, dass ein Mensch A bestimmte Ausdrücke <e1, …, ek> einer Sprache L ‚kennt‘ oder ’nicht kennt‘, dafür gibt es keine allgemeinen Regeln oder Kriterien. Von daher macht die Verwendung der Ausdrücke ‚bekannt’/ ’nicht bekannt‘ eigentlich nur Sinn in solch einem lokalen Kontexten W* (z.B. einem Artikel, ein Buch, ein Vortrag, …), in dem entscheidbar ist, ob ein bestimmter Ausdruck e einer Sprache L schon mal vorkam oder nicht. Schwierig wird es mit dem Begriff des ‚wahren Wesens‘. In meiner Interpretation mit der dynamischen Objekthierarchie gibt es ‚das wahre Wesen‘ in Form von Objekten auf einer Stufe j, die Instanzen auf Stufen kleiner als j haben. Dazu gab es weitere Überlegungen. Im folgenden Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 7 beschreibt Avicenna syntaktisch zusammengesetzte, aber semantisch einfache Ausdrücke. Innerhalb der Ausdrücke unterscheidet er die Teileausdrücke ‚Name‘, ‚Verb‘ und ‚Präposition‘. Die unterschiedliche Charakterisierung erfolgt nicht aufgrund der syntaktischen Form, sondern aufgrund der semantischen Eigenschaften, die mit diesen Ausdrücken verbunden werden. Neben dem Objektbezug, der die eigentliche Bedeutung fundiert, gibt es im Bedeutungsraum auch noch den zeitlichen und den räumlichen Aspekt. Das Zusammenspiel von Bedeutung und Ausdruck wird angerissen.

AUSSAGEN/ FESTSTELLUNGEN – WAHR oder FALSCH

2. Nun wendet sich Avicenna zusammengesetzten (engl.: ‚compound‘) ‚Aussagen‘ (engl.: ‚proposition‘) bzw. ‚Feststellungen‘ (engl.: ’statements‘) bzw. ‚bekräftigende Rede‘ (engl.: ‚affirmative speech‘) zu.
3. Stillschweigend wird hier vorausgesetzt, dass eine Aussage mit den im vorausgehenden Abschnitt charakterisierten semantischen Ausdruckstypen (Name, Verb, Präposition) realisiert ist.
4. ‚Aussagen‘ [P] sind alle jene Ausdrücke E, von denen man sagen kann, sie treffen zu (sind ‚wahr‘), oder sie treffen nicht zu (sind ‚falsch‘); Aussagen sind eine echte Teilmenge aller Ausdrücke, $latex P \subset E$.
5. Avicenna unterscheidet drei Arten von Aussagen:
6. Beispiele für ‚kategorische‘ Aussagen sind (Der Mensch)(ist)(ein Lebewesen) bzw. (Der Mensch)(ist nicht)(ein Lebewesen).
7. Beispiele für ‚Disjunktiv-konditionelle‘ (engl.:‘ ‚disjunctive conditional‘) Aussagen sind (Etwas)(ist)(dies)(oder)(jenes) bzw. (Etwas)(ist nicht)(dies)(oder)(jenes) (oder: (Es ist nicht der Fall, dass)(Etwas)(ist)(dies)(oder)(jenes).
8. Beispiele für ‚Konjunktiv-konditionelle‘ (engl.:‘ ‚conjunctive conditional‘) Aussagen sind (Wenn)(dies)(der Fall ist)(dann)(ist auch)(das)(der Fall) oder (Weil)(dies)(der Fall ist)(ist)(auch)(das der Fall) oder (Und nicht)(Wenn)(dies)(der Fall ist)(oder)(das)(der Fall ist).

DISKUSSION

WAHR/FALSCH

9. Zunächst einmal die Formulierung, ‚dass etwas der Fall sei‘ als Kriterium für die Eigenschaft ‚wahr‘ und die Formulierung ‚dass etwas nicht der Fall sei‘ als Kriterium für die Eigenschaft ‚falsch‘.
10. Aussagen bilden eine Kombination aus Ausdruck e und Bedeutungskomponente m aus dem Bedeutungsraum M.
11. Vom Sprecher/ Hörer wird angenommen, dass er die Beziehung zwischen e und m ‚kennt‘, schreiben wir K(e,m) (für die Beziehung KNOW [K] mit $latex K \subseteq E \times M$).
12. Jetzt wird gesagt, dass eine solche Beziehung K(e,m) ‚zutreffen‘ kann oder ’nicht zutreffen‘ kann, bzw. ‚wahr’/ ‚falsch‘ sein kann.
13. Dies bedeutet, es muss einen zusätzlichen Aspekt, einen zusätzlichen Umstand Y geben, wodurch ein Sprecher/ Hörer zu solch einer Charakterisierung kommen kann.
14. Dieser zusätzliche Umstand Y muss ‚veränderlich‘ sein, d.h. er muss in einem Zustand Y_w auftreten, wodurch die Beziehung K(e,m) als ‚wahr‘ bezeichnet wird, und in einem Zustand Y_f, woraus ‚falsch‘ folgt. Möglicherweise gibt es auch noch eine neutrale Variante Y_n, bei deren Vorliegen man nicht weiß, ob es die Eigenschaft ‚wahr‘ oder ‚falsch‘ zutrifft.
15. Intuitiv wissen wir, dass wir zwar mit Ausdrücken e bestimmte Bedeutungen/ Vorstellungen m verknüpfen können, wir wissen aber auch, dass solche gewussten Sachverhalte m sich in der ‚realen Welt‘ W ändern können.
16. Zuvor haben wir schon die Annahmen entwickelt, dass sich eine dynamische Objekthierarchie O mittels $latex \kappa$ angeregt von Eigenschaften X der realen Welt W bilden lässt. D.h. die Objektstruktur O, die ein Teil des Bedeutungsraumes M ist – also auch Anteile in der Bedeutung m von der Beziehung K(e,m) haben kann –, ist nicht identisch mit den Eigenschaften X der realen Welt. Die Objektstruktur O ist ein ‚konstruiertes Bild über X‘. Von daher ist es denkbar, dass das konstruierte Bild O in M als Grundlage von K(e,m) zwar unveränderlich ist – es ist, wie es ist –, dass aber die auslösenden Eigenschaften X der realen Welt sich geändert haben, und sei es nur für einen Moment (t,t‘) mit t‘ > t.
17. Man könnte nun sagen, dass Beziehungen K(e,m) die sind, bei denen der Bedeutungsanteil m in dieser Beziehung so stark von einem X in der realen Welt abhängt, dass eine ‚Änderung von X‘ als ‚Differenz‘ wahrgenommen werden kann, d.h. es wird nicht direkt ein X oder ein verändertes X verglichen, sondern nur die ‚prozessierte Form‘ vom X über die Prozesse perc() und $latex \alpha$ unter Berücksichtigung von Raum und Zeit und Anzahl. So wie das gewusste ‚m‘ einem bestimmten Xm entspricht, so würde ein ‚Nicht-Xm‘, also $latex \overline{Xm}$ in der entsprechenden Form $latex nicht-m=\alpha(perc(\overline{X}))$ als ‚verschieden‘ von m erkannt/ aufgefasst/ verstanden.
18. Anders gesagt: Wenn wir in unserm Wissen von einer Beziehung K(e,m) ‚wissen‘, bei der wir ein Bedeutungselement ‚m‘ aus M ‚kennen‘, das durch unsere Interaktion mit der realen Welt W anlässlich bestimmter realer Welteigenschaften Xm ‚konstruiert‘ werden konnte also $latex m = \lambda(\alpha(perc(Xm)),M)$, – mit $latex O \subseteq M$ –, dann würde ein von Xm verschiedener Sachverhalt $latex \overline{Xm}$ auch eine unterschiedliche Bedeutungsrepräsentation $latex \overline{m} = \lambda(\alpha(perc(\overline{Xm})),M)$ hervorbringen können. Damit könnte unser ‚Wissen‘ im allgemeinen Bedeutungsraum M die beiden Bedeutungsobjekte ‚m‘ und ‚$latex \overline{m}$‘ direkt ‚vergleichen‘.
19. Wichtig wäre bei diesem Vergleich, dass hier die Zeitkomponente eine Rolle spielt. In der gewussten Beziehung K(e,m) ist die Zeit in gewisser Weise ‚aufgehoben‘, ’neutralisiert‘, für das Vergleichsobjekt ‚m‘ bzw. ‚$latex \overline{m}$‘ müsste gelten, dass es ‚aktuell‘ ist, ‚jetzt‘. Dann könnte man sagen, wenn eine Bedeutung ‚m‘ aus einer Wissensbeziehung K(e,m) über dem Bedeutungsraum M eine Entsprechung in einem ‚aktuellen m‘ finden kann (gebunden an eine aktuelle Wahrnehmung perc()), dann korrespondiert das gewusste ‚$latex m_{K}$‘ aus K(e,m) mit dem aktuell wahrnehmbaren ‚$latex m_{now}$‘. Ist dies nicht der Fall, lässt sich keine aktuelle Entsprechung zwischen einem gewusstem ‚$latex m_{K}$‘ aus K(e,m) zu einem wahrnehmbaren ‚$latex m_{now}$‘ finden, weil die aktuellen Bedeutungen ‚$latex \overline{m}_{now}$‘ anders sind.
20. In dieser Konstruktion gibt es in der Tat nur zwei Fälle: entweder findet sich zu einem gewussten m eine aktuelle Entsprechung ‚$latex m_{now}$‘ oder eben nicht. Dazwischen gibt es nichts. Ein ’neutrales‘ m kommt hier nicht zum Tragen. Denkbar wäre allerdings ein ‚Irrtum‘ in dem Sinne, dass das aktuell wahrgenommene ‚$latex \overline{m}_{now}$‘ zwar verschieden ist, dass diese Verschiedenheit aber entweder ‚falsch eingeschätzt‘ wird oder die Konstruktion des ‚$latex \overline{m}_{now}$‘ irgendwelche ‚Störungen‘, ‚Verzerrungen‘ aufweist, so dass das ‚$latex \overline{m}_{now}$‘ einige ‚Ähnlichkeiten‘ mit dem gewussten m aufweist, die zu einem Fehlurteil führen. Denn, nicht nur kann die aktuelle Konstruktion $latex \lambda$ Fehler aufweisen, sondern auch die auf ‚Erinnerung‘ basierende gewusste Beziehung K(e,m) kann Fehler aufweisen, die das gewusste m in die Nähe des aktuellen ‚$latex \overline{m}_{now}$‘ bringen. Also, Neutralität gibt es hier nicht, aber mögliche Irrtümer unterschiedlichster Art.

AUSSAGENTYPEN

21. Nach dieser Klärung, wie die Eigenschaft ‚wahr’/ ‚falsch‘ in dieser Rekonstruktion von Avicenna nachvollziehbar wären, geht es um die Frage, was es mit den drei Aussagetypen auf sich hat, die ich hier abkürzend ‚Kategorisierend‘, ‚Disjunktiv‘ und ‚Konjunktiv‘ bezeichne.
22. Im Fall des Aussagetyps ‚Kategorisierend‘ mit dem Beispiel (Der Mensch)(ist)(ein Lebewesen) bzw. (Der Mensch)(ist nicht)(ein Lebewesen) geht es offensichtlich nicht um einen Bezug zur aktuell realen Welt mit ihren realen Eigenschaften X, sondern um eine Beziehung zwischen zwei gewussten Bedeutungsstrukturen $latex m_{Mensch}$ und $latex m_{Lebewesen}$. Zwischen diesen beiden Bedeutungsstrukturen $latex m_{Mensch}, m_{Lebewesen}$ gibt es eine Beziehung der Art, dass die Bedeutungsstruktur $latex m_{Mensch}$ eine ‚Instanz‘ der Bedeutungsstruktur $latex m_{Lewesen}$ ist. Sofern dies der Fall ist wird durch eine Aussage der Art (Der Mensch)(ist)(ein Lebewesen) genau dieser Fall angesprochen. Wenn der Ausdruck (Der Mensch)(ist)(ein Lebewesen) mit den Verhältnissen der Bedeutungsstrukturen übereinstimmt (was man direkt wissen kann), dann trifft der gewusste Sachverhalt zu, andernfalls nicht. Natürlich kann es auch in diesem Fall prozessspezifische Fehler geben, die Bedeutungszuordnungen konstruieren, die falsch sind oder missverständlich oder verändert.
23. Im Fall der disjunktiven und konjunktiven Aussagetypen ist die Lage etwas unübersichtlicher, da Avicenna keine direkte Charakterisierung der beiden Aussagetypen mittels Wahrheitswerten vornimmt. Er erwähnt nur verschiedene Ausdrücke, denen man ‚intuitiv‘ eine Bedeutung zuordnen muss, und diese Beispiele sind – bei genauer Betrachtung – sogar widersprüchlich.
24. Bedient man sich des Hilfsmittels der Wahrheitswerttabelle, die zumindest in der stoischen Logik schon bekannt gewesen sein soll, dann kann man die beiden Aussagetypen Disjunktion und Konjunktion eindeutig charakterisieren. Dazu ist es hilfreich, die Ausdrücke von Avicenna ein wenig zu ’normieren‘.
25. DISJUNKTION: Statt zu schreiben (Etwas)(ist)(dies)(oder)(jenes), würde man umschreiben A=(Etwas)(ist)(dies) und B=(Etwas)(ist)(jenes), sodass der ganze Ausdruck lauten würde (A)(oder)(B), wobei sowohl A als auch B vom Typ ‚Aussage‘ sind, die ‚wahr‘ oder ‚falsch‘ sein kann. Dann könnte man sagen, dass ein Aussagetyp ‚Disjunktion‘ nur dann wahr ist, wenn wenigstens eine der beiden Teilaussagen A oder B wahr ist bzw. nur dann falsch ist, wenn beide Teilaussagen A und B falsch sind.
26. Den Fall, den Avicenna als ‚Konjunktives Konditional‘ einführt, ist nicht eindeutig. Es könnte entweder der späteren aussagenlogischen Konjunktion entsprechen oder auch der aussagenlogischen Implikation. Seine unvollständige Charakterisierung lässt beide Rekonstruktionen zu. Ich betrachte hier beide Fälle.
27. KONJUNKTION: Statt zu schreiben (Weil)(dies)(der Fall ist)(ist)(auch)(das der Fall) würde man im Fall der Konjunktion abkürzend schreiben A=(dies)(der Fall ist) und B=(das(ist)(der Fall). Dann könnte man sagen, der Ausdruck (A)(und)(B) ist nur wahr, wenn jeder der beiden Teilaussagen A und B wahr ist, und ist falsch, wenn wenigstens einer der beiden Teilaussagen falsch ist.
28. IMPLIKATION: Der Ausdruck (Wenn)(A)(dann)(B) ist nur falsch, wenn A wahr ist und B zugleich falsch; in allen anderen Fällen ist der Ausdruck wahr.
29. Disjunktion, Konjunktion und Implikation sind also Aussagetypen, die aus zwei Teilausdrücken A und B bestehen, die selbst wieder Aussagen sind, die wahr oder falsch sein können. Die beiden Teilausdrücke A und B werden dann durch die Teilausdrücke (oder), (und) sowie (wenn)-(dann)- verknüpft. Sie unterscheiden sich dadurch, wie der Wahrheitswert des Gesamtausdrucks von der Verteilung der Wahrheitswerte auf die Teilausdrücke festgelegt ist. Die Teilausdrücke (oder), (und) sowie (wenn)-(dann)- nennt man später dann auch ‚aussagenlogische Operatoren‘.
30. Man sieht hier leicht, dass der Aussagetyp ‚kategoriesierend‘ nicht in dieses Schema passt. Der Aussagetyp ‚kategorisierend‘ ist eine Aussage A, die wahr oder falsch sein kann unabhängig von irgendeinem aussagenlogischen Operator.

NEGATION

31. Die Verneinung von Aussagen hat man später dann auch anders geschrieben.
32. Statt zu schreiben (Etwas)(ist nicht)(dies)(oder)(jenes) hat man später geschrieben $latex \neg(A)(oder)(B)$ mit dem Zeichen $latex \neg$ für ’nicht‘ oder ‚es ist nicht der Fall, dass‘. Statt (oder) wurde später auch geschrieben $latex \vee$. Statt (und) das Zeichen $latex \wedge$. Dann bekommt man $latex \neg(A)(\vee)(B)$ bzw. $latex \neg(A)(\wedge)(B)$.

ERGEBNIS

33. Diese Rekonstruktionsansätze mögen genügen, um zu verdeutlichen, dass man eine plausible Semantik zur bisherigen Logik von Avicenna dazu konstruieren und dass man seine Aussagen zu Aussagetypen mit Wahrheitswerten letztlich mit den Konzepten der modernen Aussagenlogik versöhnen kann.
34. Was hier (noch) nicht gemacht wird, das ist die sich daraus ergebenden Konsequenzen in ihrer ganzen Breite zu entwickeln. Dies wird zu einem späteren Zeitpunkt geschehen.
35. Was die Semantik angeht, so kann man natürlich die Quintessenz der Semantik in einem formalen Modell auch noch viel einfacher fassen. Allerdings liegt das Interesse hier gerade darin, es nicht einfach nur zu vereinfachen, sondern es ganz speziell auch im Hinblick auf das Alltagsdenken und mit Blick auf die kognitiven Prozesse so zu verorten, dass die ‚Entstehung der Bedeutung‘ – zumindest prinzipiell – mit erfasst wird. Die Minimalforderung lautet, dass ein Ingenieur/ Informatiker in der Lage sein sollte, mit diesem Minimalmodell einen Roboter/ Softwareagenten zu bauen, der selbstständig die Bedeutung normalsprachlicher Ausdrücke von jeder Sprache für realweltliche Kontexte W erlernen kann.

Eine Fortsetzung findet sich HIER.

QUELLEN

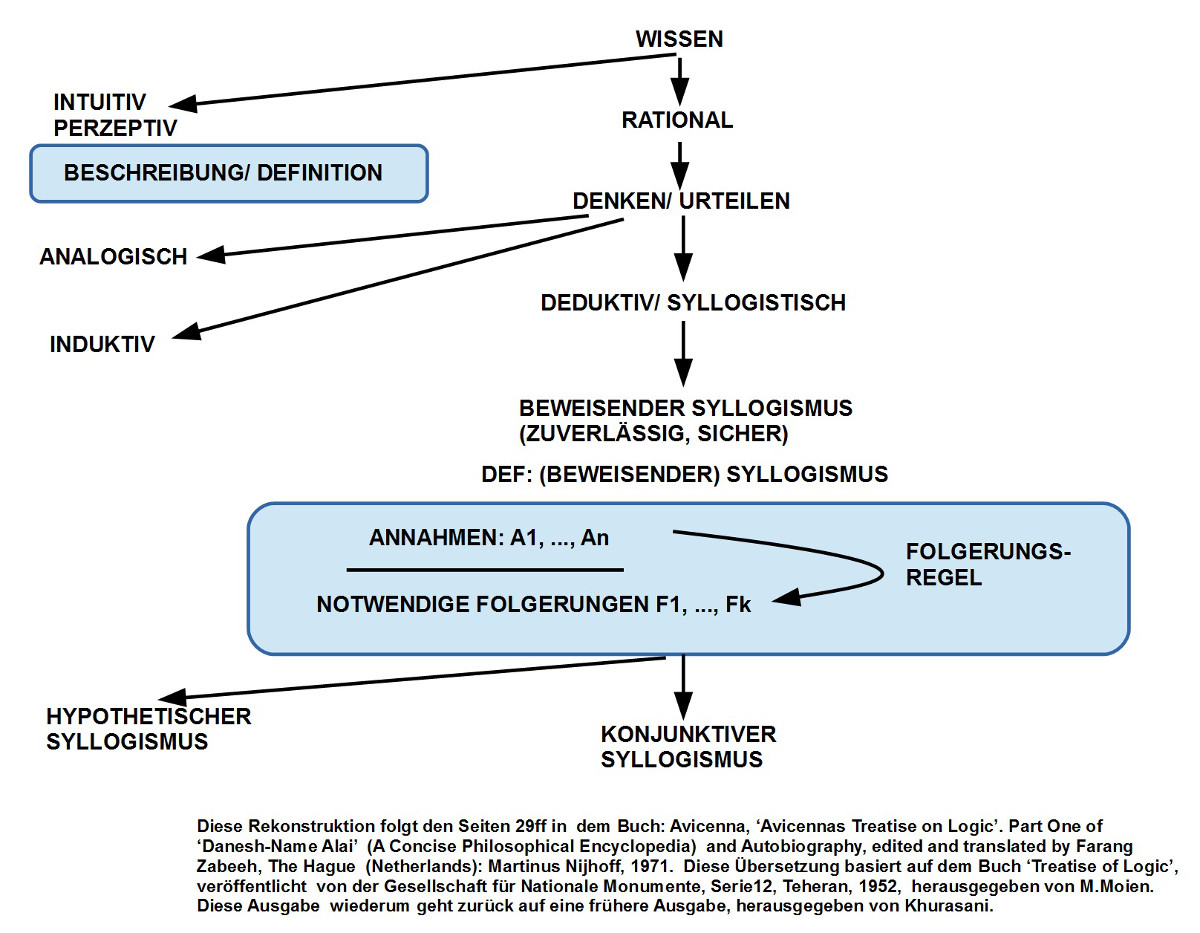
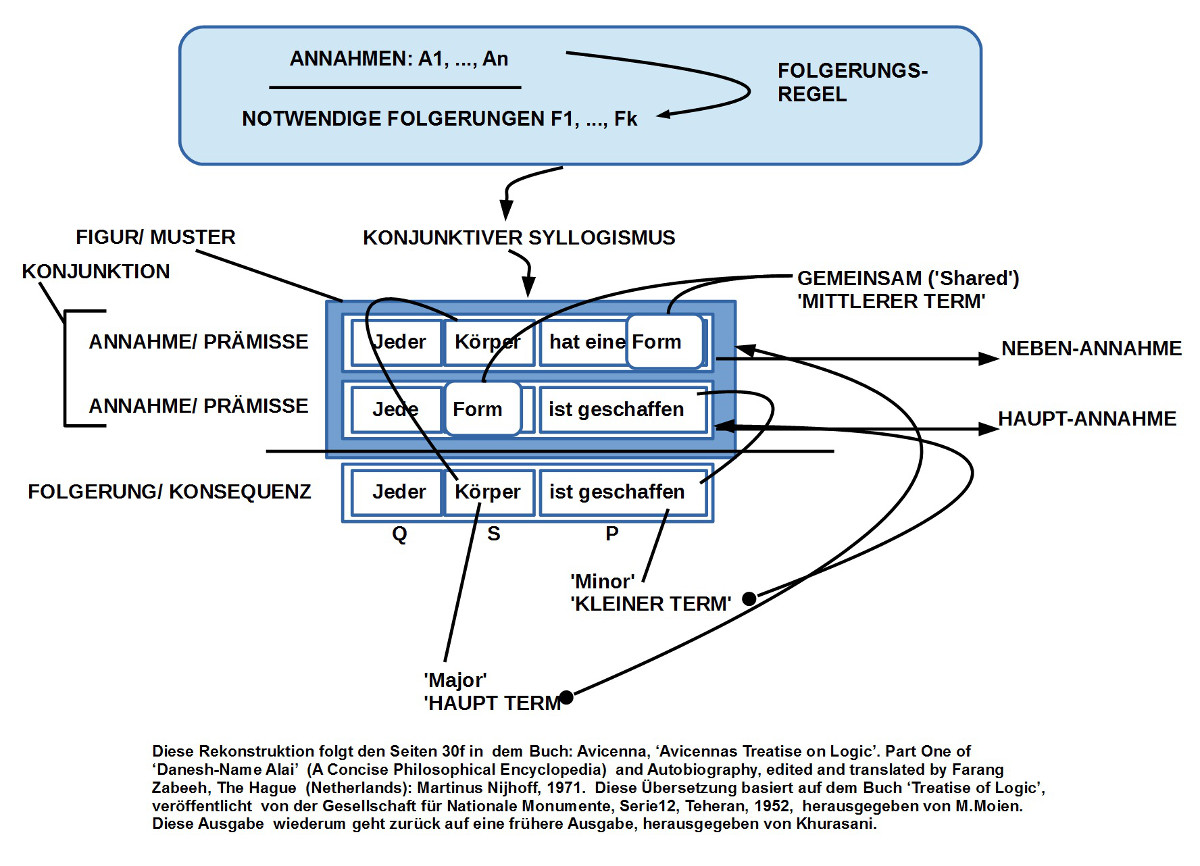
  • Avicenna, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
  • Digital Averroes Research Environment
  • Stanford Encyclopedia of Philosophy, Aristotle’s Logic
  • Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7

Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER.