Archiv der Kategorie: Philosoph

AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 11

Abstraktion, Affirmativ, Ausdruck, Ausdruck - einfacher, Ausdruck - sprachlicher, Ausdruck - zusammengesetzter, Aussage, Aussagetypen, Außenwelt, Avicenna, Logik, Logik - Alltag, Logik - Antike, Logik - formale, Objekt, Objekt - als Eigenschaft, Objekt - echtes, Objekt erkanntes, Objekt-Modell, Philosophie - Islamische, Prädikat, Quantor, Subjekt, Wahrheit, Wahrheitswert, Wahrnehmen, Wahrscheinlichkeit
Bildskizzen zu Avicennas Diskussion der Aussagetypen Disjunktive und Konjuntive Konditionale
Bildskizzen zu Avicennas Diskussion der Aussagetypen Disjunktive und Konjuntive Konditionale

VORGESCHICHTE

Für einen Überblick zu allen vorausgehenden Beiträgen dieser rekonstruierenden Lektüre von Avicennas Beitrag zur Logik siehe AVICENNAS ABHANDLUNG ZUR LOGIK – BLITZÜBERSICHT.

Aufgrund des großen Umfangs enthält dieser Blogeintrag zu Avicennas Logik – im Gegensatz zu den vorausgehenden Blogeinträgen 1-9 – nur den Diskussionsteil von Blogeintrag 10. In Blogeintrag 10 wurde weiter die Position Avicennas beschrieben. Ziel der Lektüre ist die Rekonstruktion einer möglichen Theorie der Alltagslogik, wie sie dann in künstlichen lernenden Systemen eingesetzt werden soll (hier trifft die Philosophie direkt auf die Ingenieurskunst ….; man nennt dies ‚Informatik‘).

DISKUSSION

26. Wie schon mehrfach bemerkt, erscheint die Verwendungsweise der meisten Begriffe in Avicennas Abhandlung über die Logik ‚fließen‘ oder – mit einem Begriff aus der modernen Logik – ‚fuzzy‘.

27. Dies hat damit zu tun, dass Avicenna für die Verwendung seiner Begriffe keine klaren Kriterien benutzt. Typisches Beispiel ist sein Begriff der ‚Harmonie‘, den er für die Klassifikation von Antezedenz – Konsequenz Verhältnisse benutzt. Klar ist, dass er für diesen Begriff auf die Bedeutungsdimension zurückgreift; unklar ist, wie genau er dies versteht, da das, was er praktisch überall als ‚Bedeutung unterstellt‘, nirgendwo präzisiert wird. Will man diesen Nachteil beheben, muss man einen Weg finden, die Kriterien zu klären. Ein erprobtes Mittel dafür ist, alle die Umstände explizit zu machen, zu benennen, die man als für ein Kriterium ‚relevant‘ erachtet. Dies ist in der modernen Wissenschaft eine Mischung aus kontrollierten Beobachtungen und theoretischen Annahmen. Und da keine Beobachtung einen ‚Sinn‘ ergibt ohne Bezug zu vorausgesetzten Beziehungen/ Relationen/ Strukturen/ Modellen beginnt jede Klärung eines vagen Zusammenhangs mit ersten ‚theoretischen Annahmen‘ darüber, welche Zusammenhänge man für wichtig hält, mit denen man bekannte – oder noch zu messende – Phänomene ‚erklären‘ möchte.

28. Beginnen wir mit den letzten Annahmen von Avicenna.

AUSSAGEN – AUSSAGESTRUKTUREN

29. Ausgangspunkt sind solche Ausdrücke E, die ‚wahr‘ oder ‚falsch‘ sein können; er nennt sie ‚Aussagen‘ [PROP]: $latex PROP \subseteq E$.
30. Aus logischer Sicht hat Avicenna bislang vier funktionale Rollen innerhalb einer Aussage unterschieden: ‚Subjekt‘, ‚Prädikat‘, ‚Aussageoperatoren‘ sowie ‚Quantoren‘.
31. Minimal benötigen wir ‚Subjekt‘ S und ‚Prädikat‘ P, so dass man im Prädikat P etwas über das Subjekt S aussagen kann: $latex (S P)$
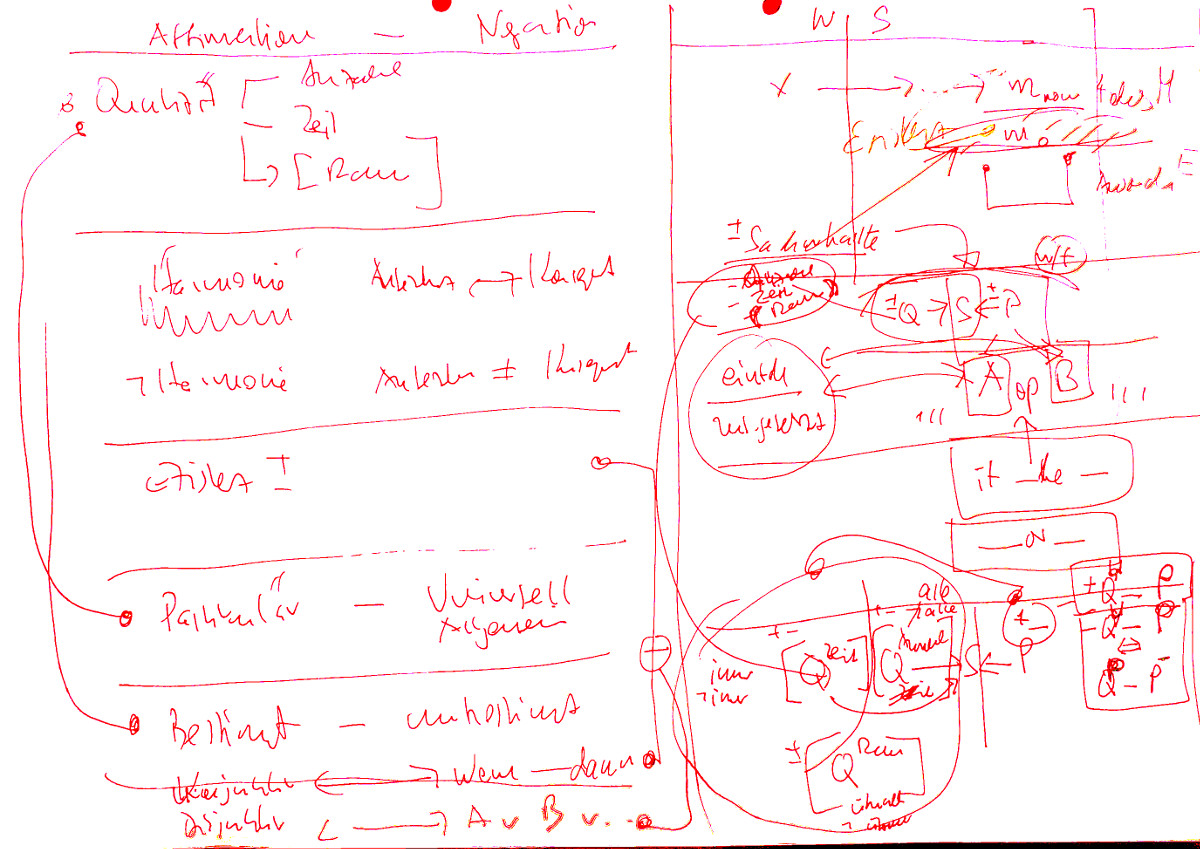
32. Zusätzlich gibt es die Rolle der logischen ‚Aussage-Operatoren‘ ‚Negation‘ $latex \neg$, ‚Exklusive Disjunktion‘ (auch ‚Kontravalenz‘ oder ‚X-OR‘) $latex \sqcup$, und ‚Quantoren‘ Q. Hier unterscheidet er Quantoren über die ‚Anzahl‘ $latex Q_{q}$, und Quantoren über die ‚Zeit‘ $latex Q_{t}$. Man solle gleich noch die Quantoren über den ‚Raum‘ $latex Q_{s}$ ergänzen; diese erwähnt er nicht explizit, aber im Bereich des Bedeutungsraumes spielt die Dimension des Raumes eine wichtige Rolle und begegnet uns in sehr vielen Aussagen.
33. Bei der Verwendung von Quantoren bezieht man sich immer auf eine Gesamtheit. Im Falle von Zeit-Quantoren $latex Q_{t}$ sind dies Zeitpunkte angeordnet auf einem Zeitstrahl. Im Falle von Anzahl-Quantoren $latex Q_{q}$ bezieht man sich auf die Objekte, zu denen das Subjekt einer Aussage in einer Beziehung steht; im Falle von Raum-Quantoren $latex Q_{s}$ bezieht man sich auf zu definierende ‚Raumstellen‘.
34. Unter der Voraussetzung, dass eine Aussage A = (S P) ‚wahr‘ oder ‚falsch‘ sein kann, kann man sagen, dass $latex \neg A$ ‚wahr‘ ist, wenn ‚A‘ alleine ‚falsch‘ ist, d.h. wenn die Aussage A= (S P) nicht zutrifft; d.h. $latex (S \neg P)$ trifft zu.
35. Die Aussage ‚Entweder A oder B‘ $latex (A \sqcup B)$ ist ‚wahr‘, wenn entweder A wahr und B falsch ist oder B wahr und A falsch. Die Verneinung von $latex \neg(A \sqcup B)$ ist wahr, wenn entweder A und B zusammen wahr oder zusammen falsch sind.
36. Die Aussage ‚Wenn A dann B‘ $latex (A \rightarrow B)$ ist nur dann falsch, wenn A zutrifft und zugleich B falsch ist. In allen anderen Fällen ist die Implikation wahr. Die Verneinung $latex \neg(A \rightarrow B)$ wäre dementsprechend wahr, wenn A wahr wäre und B nicht; in allen anderen Fällen falsch
37. Es sei angemerkt, dass die Implikation $latex (A \rightarrow B)$ äquivalent ist zu $latex \neg(A \wedge \neg B)$, wobei das Zeichen ‚$latex \wedge$‘ den aussagenlogischen Operator ‚Konjunktion‘ (‚und‘) repräsentiert. $latex (A \wedge B$ sind nur wahr, wenn A und B zugleich wahr sind, sonst falsch.
38. Quantoren werden Aussagen vorangestellt, also (Q A) bzw. (Q (S P)).
39. Anzahl-Quantoren $latex Q_{q}$ wären ‚alle‘ und verneint $latex \neg Q_{q}$ ’nicht alle‘, definiert durch ‚einige := nicht alle‘.
40. Zeit-Quantoren $latex Q_{t}$ wären ‚immer‘ und verneint $latex \neg Q_{t}$ ’nicht immer‘, definiert durch ‚manchmal := nicht immer‘.
41. Raum-Quantoren $latex Q_{s}$ wären ‚überall‘ und verneint $latex \neg Q_{s}$ ’nicht überall‘, definiert durch ‚einige := nicht überall‘.
42. Als Schreibweisen hat sich herausgebildet, im Falle von ‚alle’/ ‚immer’/ ‚überall‘ von ‚All-Quantoren‘ zu sprechen und zu schreiben $latex \forall(x)$. Das ‚x‘ steht dann für die Art von Objekten, über deren Gesamtheit quantifiziert wird. Im Fall von ‚einige’/ ‚manchmal“ spricht man von ‚Partikularquantoren‘ (missverständlich auch ‚Existenzquantoren‘) und schreibt $latex \exists(x)$. Das ‚x‘ steht wieder für die Art von Objekten, über deren Gesamtheit quantifiziert wird.
43. Im Falle von Partikularquantoren von ‚Existenzquantoren‘ zu sprechen ist leicht irreführend, da ein Existenzquantor $latex \exists(x)$ keine Aussage über die reale Existenz in der umgebenden Welt W trifft, sondern nur angibt, über wie wieviele Objekte x einer Art gesprochen werden soll.
44. Beispiel: ‚Manchmal ist der Himmel grau‘ $latex \exists(t)(der Himmel)(t)(ist grau)$. Es gibt einige Zeitpunkte t (aus der Gesamtheit der geordneten Zeitpunkte T), an denen vom Himmel gesagt werden kann, dass er grau ist.
45. Beispiel: ‚Überall scheint die Sonne‘ $latex \forall(s)(die Sonne)(scheint)$. An allen Raumpunkten s (aus der Gesamtheit der Raumpunkte S), kann von der Sonne gesagt werden kann, dass sie scheint.
46. Beispiel: ‚Alle Menschen sind sterblich‘ $latex \forall(x)(Menschen)(sind sterblich)$. Für alle Objekte aus der Gesamtheit der Menschen kann gesagt werden, dass sie sterblich sind.
47. Beispiel: ‚Nicht alle Menschen sind sterblich‘ $latex \neg\forall(x)(Menschen)(sind sterblich)$ wird übersetzt $latex \exists(x)(Menschen)(sind nicht sterblich)$, $latex \exists(x)(S)(\neg P)$, d.h. für einige Objekte aus der Gesamtheit der Menschen kann gesagt werden, dass sie nicht sterblich sind.

WAHRHEITSBEDINGUNGEN – BEDEUTUNGSRAUM

48. Mit der Einführung der Begriffe ‚Aussage‘, ‚Subjekt‘, ‚Prädikat‘, ‚Aussage-Operator‘, ‚Quantor‘ wurden Strukturelemente von Ausdrücken beschrieben. Allerdings wurde bei der ‚Charakterisierung‘ der unterschiedlichen logischen Rollen immer schon – mehr oder weniger explizit – Bezug genommen auf einen unterstellten ‚Bedeutungsraum‘ M.
49. Der wichtige Punkt hier ist, dass man den Unterschied zwischen dem Bedeutungsraum M und den Eigenschaften X der umgebenden Welt W beachtet.
50. Wie schon zuvor herausgestellt, ist der Bedeutungsraum M, auf den sich die Aussagen mit ihren Strukturen primär beziehen, zu einem gewissen Teil eine Konstruktion über bestimmten Ereignissen X in der umgebenden Welt W.
51. Dieser Unterschied ist die Voraussetzung für Begriffe wie z.B. ‚Existenz‘, ‚wahr’/ ‚falsch‘ und ‚möglich‘.
52. Denn mittels einer Aussage A bestimmte Bedeutungselemente $latex m \subseteq M$ zu benennen, zu aktivieren, ist zwar eine Grundvoraussetzung dafür, dass ein Ausdruck e als Aussage A überhaupt eine ‚Bedeutung‘ hat, diese Bedeutungselemente m sind als solche aber weder ‚wahr‘ noch ‚falsch‘; ihre ‚Existenz‘ ist unklar; ob sie ‚real‘ oder ‚möglich‘ sind folgt aus der primären Bedeutung nicht.
53. Erst wenn man davon ausgeht, dass es innerhalb des Bedeutungsraumes M solche Bedeutungselemente m* gibt, die sich von anderen Bedeutungselementen m0 dadurch unterscheiden, dass ihnen ein ‚Aktualitätsbezug‘ zu aktuellen Wahrnehmungen zusprechen kann, nur dann kann es ein Kriterium geben, wodurch eine Aussage A ’nur‘ eine ‚wahrheitsneutrale‘ Bedeutung m0 hat oder eben durch die ‚Aktualitätseigenschaft‘ m* als ‚zutreffend in der umgebenden Welt M‘ charakterisiert werden kann. An dieser Eigenschaft des ‚aktuell Zutreffens‘ in der umgebenden Welt W lassen sich die Begriffe ‚wahr‘ und ‚falsch‘ ‚anhängen‘: gibt es eine Bedeutung m0, die eine hinreichende Ähnlichkeit mit einer Bedeutung m* hat, dann kann man von der Aussage, die die Bedeutung m0 bezeichnet, sagen, dass sie ‚zutrifft‘ und damit ‚wahr‘ ist; gibt es zu einer aktuell bezeichneten Bedeutung m0 einer Aussage A keine hinreichend ähnliche Bedeutung m*, dann trifft die Bedeutung m0 der Aussage A nicht zu, d.h. sie ist falsch.
54. Sofern wir über ‚Erinnerungen‘ an Bedeutungen m(m*) verfügen, die zu ‚vorausgehenden Zeitpunkten‘ einmal ‚wahr‘ waren, kann dieses Wissen m(m*) dazu benutzt werden, um eine ‚Erwartung‘ über die umgebenden Welt W aufzubauen, dass der Sachverhalt m(m*) sich als aktuelle Wahrnehmung m* ‚reproduzieren‘ lässt; dafür, dass dem so ist, gibt es keine ‚Garantie‘; selbst die sogenannten ‚Naturgesetze‘ sind keine 100%ige Garantie dafür, dass eine erinnerbare Eigenschaft m(m*) aufgrund ihres ‚früheren‘ Auftretens als m* nochmals als m* auftreten wird.

MÖGLICH

55. Ich würde den Begriff der Möglichkeit auch an dieser Differenz aufhängen: einerseits ‚aktuell wahrgenommene‘ Bedeutungselemente m* bzw. ‚erinnert als schon mal aktuell wahrgenommen‘ m(m*)‘ und andererseits nur ‚gedacht’/ ‚vorstellbar‘ als m0 ohne Entsprechung zu einem m* bzw m(m*). Eine ‚Differenz‘ zwischen allgemein vorstellbar/ denkbar und aktuell wahrnehmbar bzw. erinnert als aktuell mal wahrgenommen ist generell ein Hinweis auf Möglichkeit. Wie ‚wahrscheinlich‘ solche möglichen Bedeutungselemente m0 mal als m* reproduziert werden können, ist allgemein kaum anzugeben. Basierend auf dem bislang verfügbaren erinnerbaren Wissen M(M*) insgesamt kann man zwar gewisse ‚Erwartungen‘ konstruieren; dies können aber – wie wir aus der Geschichte wissen – unzuverlässig sein, da sie auf falschen Annahmen bzw. Interpretationen beruhen können (‚Sonne bewegt sich um die Erde‘ oder ‚Erde bewegt sich um die Sonne‘).

WELT ALS FIKTION

56. Aus der bisherigen Rekonstruktion folgt, dass der Begriff der ‚umgebenden Welt W‘ streng genommen eine ‚Fiktion‘ ist. Was es gibt, sind Erregungszustände m* im Gehirn, die es zum überwiegenden Teil nicht selbst verursacht; sie werden in die Erregungsmenge des Gehirns ‚induziert‘. Verglichen damit sind die anderen (bewussten) Erregungszustände m0 ‚von innen‘ (endogen) erzeugt. Unser Gehirn nimmt diese nicht-selbst induzierten (bewussten) Erregungszustände m* als ‚etwas von ihm Verschiedenes‘, an dem sich viele ‚Eigenschaften‘ unterscheiden lassen, u.a. auch eine implizite Raumstruktur. Der Begriff der ‚Welt‘ ist in diesen nicht-selbst induzierten Erregungszuständen m* fest gemacht. Als m* sind diese Erregungszustände ‚unmittelbar‘, ‚direkt‘, so, als ob wir die ‚Welt‘ ‚direkt‘ erleben würden. Wie wir aber heute wissen (können), sind diese direkt erlebbaren Erregungszustände m* das ‚Produkt‘ eines komplizierten Übersetzungsmechanismus, den wir sinnliche Wahrnehmung perc() nennen. Im Prozess der sinnlichen Wahrnehmung perc() werden einige der Weltereignisse X in sinnliche Zustände $latex m_{p}$ abbgebildet: $latex perc: X \longrightarrow M_{p}$. Zusätzlich wissen wir heute, dass die schon verfügbaren Bedeutungselemente M auf diesen Wahrnehmungsprozess Einfluss nehmen können (Stichwort ‚Erwartungen‘, ‚Vorurteile‘ , …): $latex perc: X \times M \longrightarrow M_{p}$.
57. Dabei sind es normalerweise nicht die sinnlichen Erregungszustände $latex M_{p}$, die wir wahrnehmen, sondern die Objekte der nächsten Verarbeitungsstufe, die aus den sinnlichen Elementen als Objektelemente heraus abstrahiert werden: $latex \alpha: M_{p} \times M \longrightarrow M_{o}$. Auch hier wirken sich die schon vorhandenen Bedeutungselemente M auf den Abstraktionsprozess aus. Statt $latex M_{o}$ wird hier auch verkürzend oft nur von den ‚Objekten‘ O gesprochen, da Objekte immer nur als Elemente des Bedeutungsraumes M vorkommen.
58. Die zuvor erwähnten aktuellen Wahrnehmungen m* sind eine Teilmenge der Objektelementen $latex M_{o}$, also $latex m* \subseteq M_{o}$. Die Objektelemente ohne die aktuellen Wahrnehmungen m* gehören zu den ‚denkbaren‘ Objektelementen, also $latex (M_{o} – m*) \subseteq M0$. Dies ist möglich, weil im Gehirn ja nicht ‚reale‘ Objekte mit ‚gedachten‘ Objekten verglichen werden, sondern die ‚realen‘ Objekte treten im Gehirn schon als ‚gezähmte‘ Objekte auf, d.h. was immer an Eigenschaften X in der realen Welt W zur Konstruktion der aktuellen Wahrnehmungen m* geführt hat, m* selbst ist ein Konstrukt wie m0 auch. Deswegen lassen sich beide ‚vergleichen‘ und mit den Mitteln des ‚Denkens‘ ‚bearbeiten‘.

ERGEBNISSE

59. An dieser Stelle könnte man jetzt eine eigene große Abhandlung zur Alltagslogik schreiben. Um den Gang der weiteren Untersuchung von Avicennas Abhandlung damit aber nicht vollständig zu sprengen, beende ich hier die rekonstruierenden Überlegungen und wende mich wieder der Lektüre des Textes zu. Wie man sieht, kann solch eine Lektüre extrem anregend sein.

AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 10

Avicenna, Logik, Logik - Alltag, Logik - Antike, Logik - formale
Bildskizzen zu Avicennas Diskussion der Aussagetypen Disjunktive und Konjuntive Konditionale
Bildskizzen zu Avicennas Diskussion der Aussagetypen Disjunktive und Konjuntive Konditionale

VORGESCHICHTE

Für einen Überblick zu allen vorausgehenden Beiträgen dieser rekonstruierenden Lektüre von Avicennas Beitrag zur Logik siehe AVICENNAS ABHANDLUNG ZUR LOGIK – BLITZÜBERSICHT.

Dieser Blogeintrag beginnt mit einer Darstellung der Position von Avicenna und diskutiert dann im Abschnitt ‚DISKUSSION‘ Avicennas Position. Ziel der Lektüre ist die Rekonstruktion einer möglichen Theorie der Alltagslogik, wie sie dann in künstlichen lernenden Systemen eingesetzt werden soll (hier trifft die Philosophie direkt auf die Ingenieurskunst ….; man nennt dies ‚Informatik‘).

AVICENNAs DISKUSSION DES DISJUNKTIVEN UND DES KONJUNKTIVEN KONDITIONALS

1. Anstatt jetzt einzelne Stellen aus dem Text (SS.24-27) zu zitieren hier eine reflektierende Zusammenfassung seiner Aussagen.

AUSDRÜCKE, DIE AUSAGEN SIND

2. Der übergreifende Zusammenhang seiner Überlegungen bilden solche Ausdrücke, die als ‚Aussagen‘ bestimmte Sachverhalte beschreiben, die ‚wahr‘ oder ‚falsch‘ sein können.

3. Das grundsätzliche Kennzeichen solcher Aussagen ist, dass sie von etwas ‚affirmierende‘ (zustimmend, bekräftigend, …) sagen, dass es sich so verhalte, wie gesagt.

QUANTOR SUBJEKT PRÄDIKAT (Q S P)

4. Eine Aussage kann man entweder mit ‚grammatischen‘ Begriffen analysieren im Sinne von ‚Name Verb Präposition Name‘ (z.B. ‚Zyd ist im Haus‘) oder mit logischen Begriffen wie ‚Quantor Subjekt Prädikat‘ (Q S P).

5. Das Subjekt S ist dasjenige, von dem/ über das etwas ausgesagt wird, das im Prädikat P formuliert wird. Der Quantor Q klärt, ob es ‚universell‘ (z.B. ‚alle‘) gemeint ist oder ‚partikulär‘ (z.B. ’nicht alle‘ als ‚einige‘).

EXISTENZ

6. Avicenna benutzt auch bisweilen den Begriff ‚Existenz’/ ‚existieren‘ im Kontext, dass der Sachverhalt einer Aussage ‚existiert‘ oder ’nicht existiert‘, ohne die Verwendung des Begriffs ‚existieren‘ explizit zu analysieren.

EXISTENZ, AFFIRMATION, VERNEINUNG

7. Das Wechselspiel zwischen den Begriffen ‚Affirmieren/ Affirmation‘, ‚Verneinung‘ sowie ‚Existenz‘ ist nicht ganz klar. Einerseits kann die Verneinung eines Sachverhaltes (S nicht P) dennoch eine Affirmation sein, d.h. der Sprecher will damit sagen, dass es zutrifft, dass nicht-P auf S zutrifft, andererseits wird die Verneinung manchmal so verwendet, als ob damit grundsätzlich die Affirmation aufgehoben würde. Einerseits wird ein Ausdruck der Art (S nicht P) interpretiert, dass das ’nicht-P‘ existiert als Eigenschaft von S, dann aber wieder soll das ’nicht‘ in P die ‚Existenz von P‘ aufheben.

BESTIMMT – UNBESTIMMT

8. Auch benutzt Avicenna den Begriff ‚bestimmt/ nicht bestimmt‘ im Kontext der Verwendung von Quantoren. So sagt er z.B. dass (Alle S sind P) ‚bestimmt‘ sei in der Bedeutung, (Nicht-Alle S sind P) aber ’nicht bestimmt‘ als ‚unbestimmt‘. Auch im Kontext der Verwendung von logischen Operatoren (siehe unten) taucht dieses Begriffspaar nochmals auf.

DISJUNKTIVE UND KONJUNKTIVE KONDITIONALE

9. Damit kommen wir zum Hauptthema dieses Abschnitts: ‚Disjunktive und Konjunktive Konditionale‘.

10. Was ein disjunktives oder ein konjunktives Konditional ist erklärt er nicht durch eine explizite Definition innerhalb einer Theorie, sondern durch Beispiele von Ausdrücken, die er (mittels impliziter semantischer Kriterien) so oder so charakterisiert/ klassifiziert.

11. Grundbausteine bleiben die Aussagen (Q S P), die wahr oder falsch sein können. Solche Aussagen kann man auch mit Buchstaben ‚A‘, ‚B‘ abkürzen, was Avicenna selbst im vorausgehenden Text einmal getan hat. Dabei gibt es zwei Fälle: (i) Aussagen ohne Quantoren wie A=(S P) (z.B. ‚Zid lacht‘), oder (ii) Aussagen mit Quantoren A=(Q S P) (z.B. ‚Alle Menschen sind sterblich‘).

QUANTOREN: ANZAHL – ZEIT

12. Er führt dann zwei Arten von logischen Quantoren ein: (i) (Entweder … Oder …) bzw. (ii) (Wenn … dann …). Fall (i) nennt er ‚Disjunktives Konditional‘ und Fall (ii) ‚Konjunktives Konditional‘ (in der späteren modernen Aussagelogik versteht man unter ‚Konjunktion‘ etwas anderes; Fall (ii) von Avicenna heißt in der modernen Aussagenlogik ‚Exklusives Oder‘ oder ‚Kontravalenz‘). Eine moderne Schreibweise für (Wenn A dann B) wäre ($latex A \rightarrow B$), und für (Entweder A oder B) die Schreibweise ($latex A \sqcup B$)).

HARMONIE – DISHARMONIE

13. Interessant ist, dass Avicenna seine logischen Operatoren nicht mit Hilfe sogenannter Wahrheitstafeln (Wahrheitsfunktionen) explizit charakterisiert, sondern aus einer Mischung von Wahrheitswertzuordnungen und den Begriffen ‚Harmonie/ Disharmonie‘.

ANTEZEDENZ – KONSEQUENZ

14. Dazu benötigt er noch zwei Zusatzbegriffe, nämlich die Begriffe ‚Antezedenz‘ und ‚Konsequenz‘. Im Beispiel (Wenn A dann B) kann man nach Avicenna das ‚A‘ als Antezedenz‘ von der Konsequenz ‚B‘ sehen. Im Beispiel (Entweder A oder B) ist es eigentlich nicht klar, welche Komponente das Antezedenz sein soll. Avicenna optiert dafür, dass der ‚linke Teil‘, also ‚Entweder A‘ ein Antezedenz sei, gesteht aber zu, dass es in diesem Fall viele Konsequenzen geben könnte, also (Entweder A oder B1 oder B2 …).

15. Kombiniert mit den Begriffen ‚Harmonie’/ ‚Disharmonie‘ befinden sich die Ausdrucksteile ‚A‘ und ‚B‘ im Fall (Wenn A dann B) in ‚Harmonie‘ (‚Wenn‘ (‚die Sonne‘ ‚aufsteigt‘), ‚dann‘ (‚es‘ ‚ist‘ Tag‘)). B soll hier nach Avicenna von A abhängen. Zu sagen (Wenn (‚es‘ ‚ist‘ ‚Tag‘) dann (‚die Sonne‘ ’steigt auf‘)) würde nach Avicenna disharmonisch sein. Im Falle einer Disjunktion (Entweder A oder B) sei dies aber nicht so. Zwischen dem Antezedenz ‚A‘ und den verschiedenen möglichen Konsequenzen ‚B1‘, ‚B2‘, … besteht keine Harmonie; man kann ihre Anordnung im Ausdruck ändern, ohne dass sich der gemeinte Sachverhalt ändert.

16. Unklar bei Avicenna ist allerdings, ob man nur innerhalb der Konsequenzen ‚B1‘, ‚B2’… umstellen kann bei Beibehaltung des ‚A‘ als Antezedenz oder ob man generell umstellen könnte, also (Entweder ‚B3‘ oder ‚B1‘ oder ‚A‘ oder …).

17. Generell ist die Verwendungsweise der logischen Begriffe bei Avicenna durchgehend ‚fließend‘, d.h. aufgrund seiner generell vagen Charakterisierungen der Begriffe kommt es ständig zu ‚Vermischungen‘ von Verwendungsweisen, die ‚verwirren‘ können. So stellt er einmal die Frage, wie denn das Verhältnis der Begriffe ‚Antezedenz – Konsequenz‘ zu den Begriffen ‚Subjekt S – Prädikat P‘ sei. Würde man berücksichtigen, dass die Begriffe ‚S- P‘ die ‚innere Struktur‘ eines Ausdrucks analysieren, der eine Aussage ist, und die Begriffe ‚Antezedenz‘ – ‚Konsequenz‘ das Verhältnis zwischen Aussagen analysieren, dann würde man diese Frage gar nicht stellen. Die Tatsache aber, dass Avicenna diese Frage aufwirft, zeigt, dass er für sich diese Verwendungsweisen nicht so klar abgegrenzt hat.

18. So kommt Avicenna zu der Deutung, dass in einem Ausdruck der Art (Wenn A dann B) die Verbindung von ‚Wenn‘ mit ‚A‘ aus der Aussage A (die wahr oder falsch sein kann), mit ‚Wenn A‘ ein Ausdruck entsteht, der nicht mehr wahr oder falsch sein kann und daher keine eigentliche Aussage mehr ist. Das gleiche gelte für das Konsequenz ‚dann B‘; auch wenn ‚B‘ für sich wahr oder falsch sein kann, in der Kombination ‚dann B‘ ist der neue zusammengesetzte Ausdruck weder wahr noch falsch und damit keine Aussage.

19. Auf den ersten Blick hat Avicenna Recht, da die beiden Ausdrücke ‚Wenn A‘ und ‚dann B‘ isoliert voneinander, nach den bisherigen Regeln keinen Wahrheitswert haben können. Aber das ‚Wesen‘ eines zusammengesetzten Ausdrucks, dessen Teile über logische Operatoren verbunden sind, besteht ja gerade darin, dass sich der Wahrheitswert des zusammengesetzten Ausdrucks aus den Wahrheitswerten der Teilausdrücke ergeben soll, vorausgesetzt, alle Teilausdrücke sind jeweils für sich Aussagen. Also im Ausdruck (Wenn A dann B) wäre der Wahrheitswert des gesamten Ausdrucks zu berücksichtigen, nicht seiner isolierten modifizierten Teile ‚Wenn A‘ bzw. ‚dann B‘.

20. Avicenna selbst bemerkt, dass der Zusammenhang zwischen (S P) in einer Aussage A=(S P) verschieden ist von dem Zusammenhang von Aussagen in einem zusammengesetzten logischen Ausdruck (Entweder A oder B). Während in der Aussage A das Prädikat P etwas über das Subjekt S aussagt, muss zwischen der Aussage B und der Aussage A in (Entweder A oder B) inhaltlich kein Zusammenhang bestehen. Dennoch bleibt er bei seinen ‚fließenden‘ Verwendungsweisen.

ZEITQUANTOREN

21. Innovativ erscheint seine Benutzung von ‚Quantoren über die Zeit‘. Bislang hatte er ‚Quantoren über die Anzahl‘ benutzt wie ‚alle‘ und ’nicht alle’/ ‚einige‘.

22. Quantoren über die Anzahl: Eine Aussage (alle S sind P) mit dem Quantor Q=’alle‘ nennt er ‚universell‘; eine Aussage (nicht alle S sind P) mit dem Quantor Q=’nicht alle‘ nennt er ‚partikulär‘ (und qualifiziert sie als ‚unbestimmt‘ bzgl. des Wahrheitswertes).

23. Bei Quantoren über die Zeit setzt er implizit eine Art Folge von Zeitpunkten T voraus, so dass man von zwei Zeitpunkten (t,t‘) immer sagen kann, ob t ‚früher‘, ‚gleich‘ oder ’später‘ zu t‘ ist. Ein möglicher Zeitquantor könnte sein ‚immer‘ bzw. ’nicht immer‘ als ‚manchmal‘.

24. Behält man die Struktur (Q S P) bei mit A=(S P) und (Q A), dann gibt es jetzt im Fall von zusammengesetzten logischen Aussagen wieder zwei Möglichkeiten: Entweder (i) die Quantoren sind an die einzelnen Aussagen gebunden (z.B. ‚Wenn (Q A) dann (Q B)‘) oder sie erstrecken sich über mehr als eine Aussage (z.B. ‚Q Wenn A dann B). Avicenna scheint nur den Fall (ii) zu berücksichtigen. Ein Beispiel: (Q Wenn A dann B) als ‚Manchmal Wenn A dann B‘ mit A=’Die Sonne geht auf‘, B=’Es gibt Wolken‘.

DISKUSSION

Wegen des großen Umfangs habe ich die Diskussion dieser Überlegungen von Avicenna in einen nächsten Blogeintrag ausgelagert.

Zur Fortsetzung bitte hier klicken.

QUELLEN

  • Avicenna, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
  • Digital Averroes Research Environment
  • Nicholas Rescher (1928 – ),The Development of Arabic Logic. University of Pittsburgh Press, 1964
  • Stanford Encyclopedia of Philosophy, Aristotle’s Logic
  • Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7

Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER.

AVICENNAS ABHANDLUNG ZUR LOGIK – BLITZÜBERSICHT

Allgemein, Allquantor, Alltagssprache, Analytisch, Annahme, Art (Spezies), Ausdruck, Ausdruck - einfacher, Ausdruck - sprachlicher, Ausdruck - zusammengesetzter, Aussage, Aussagetypen, Außenraum zum Körper, Außenwelt, Avicenna, Bedeutung, Bedeutung - akzidentell, Bedeutung - empirisch, Bedeutung - kontingent, Bedeutung - wesentliche, Bedeutung eines Wortes, Bedeutungsbeziehung, Bedeutungskorrelat, Bedeutungsraum, Begriffe, Definiendum, Definiens, Definition, Definition - explitite, Definition - rekursive, Definition - simultane, Denken, Eigenschaft, Erinnerung, Evolution - biologische, Evolution - kognitive, Externe Welt, Folgern - logisches, Folgerung, Logik, Logik - Alltag, Logik - Antike, Logik - formale, Prädikat, Prämisse, Subjekt, Subjekt - logisches, Syllogismus, Syllogismus - Konjunktiver, Term

(Letzte Änderung 14.Okt.2014, 06:11h )

Da die rekonstruierende Lektüre zu Avicennas Abhandlung zur Logik ein immer größeres Ausmaß annimmt, erweist sich die Methode, jeden einzelnen Beitrag mit einem Überblick über die vorausgehenden Beiträge einzuleiten, als immer weniger praktikabel. Deswegen wird jetzt ein eigener Blogeintrag als Referenzpunkt für diesen Überblick gewählt. Dies bedeutet, dass künftig alle nachfolgenden Beiträge einleitend (für die ‚Vorgeschichte‘), auf diesen Blogeintrag verweisen werden. Es ist zu beachten, dass diese Übersicht nur eine Übersicht über die wichtigsten Begriffe und Themen ist ohne alle Details und normalerweise auch ohne die ausführliche Diskussion von Avicennas Gedanken. Diese finden sich nur in den Blogeinträgen selbst, auf die verwiesen wird.

1. In einem ersten Beitrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 1 hatte ich geschildert, wie ich zur Lektüre des Textes von Avicenna gekommen bin und wie der Text grob einzuordnen ist.

2. In einem zweiten Beitrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 2 ging es um die Frage, warum überhaupt Logik? Avicenna führt erste Unterscheidungen zu verschiedenen Wissensformen ein, lässt aber alle Detailfragen noch weitgehend im Dunkeln.

3. Im Teil AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 3 ging es um einfache und zusammengesetzte Begriffe, und bei den einfachen Begriffen um ‚individuelle‘ und ‚universelle‘. Schon hier zeigt sich der fundamentale Unterschied zwischen der antiken und der modernen-formalen Logik. In der antiken Logik wird die Ausdrucksebene E – und einer sich daran manifestierenden Folgerungslogik – immer in Verbindung mit einer zugehörigen Bedeutungsstruktur gesehen, die sich an einer Objektstruktur O festmacht. Die moderne formale Logik kennt zwar auch ‚Semantiken‘ und ‚Ontologien‘, diese sind aber ’sekundär‘, d.h. es werden nur solche ‚formalen Semantiken‘ betrachtet, die zum vorausgesetzten syntaktischen Folgerungsbegriff ‚passen‘. Dies sollte dann später an konkreten Beispielen diskutiert werden. Hier liegt der Fokus auf der antiken Logik im Sinne Avicennas.

4. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 4 knüpft Avicenna an den zuvor eingeführten Begriff des ‚universellen‘ Begriffs an und betrachtet jetzt solche als ‚universell‘ bezeichneten Ausdrücke in einem Ausdruckskontext von aufeinanderfolgenden Ausdrücken. Alle diese Ausdrücke könnte man im Sinne der antiken Logik auch als ‚Urteile‘ bezeichnen, durch die einem bestimmten Ausdruck durch andere Ausdrücke bestimmte Bedeutungen (Eigenschaften) zu- oder abgesprochen werden. Hier unterscheidet er die Fälle eines ‚wesentlichen‘ Zusammenhanges zwischen zwei Begriffen und eines ’nicht wesentlichen‘ – sprich ‚akzidentellen‘ – Zusammenhangs.

5. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 5 führt Avicenna eine Reihe von neuen technischen Begriffen ein, die sich nicht alle in ihrer Bedeutung widerspruchsfrei auflösen lassen. Es handelt sich um die Begriffe ‚Genus‘, ‚Spezies‘, Differenz, allgemeine und spezielle Akzidens, den Begriff ‚Kategorie(n)‘ mit den Kategorien ‚Substanz‘, ‚Qualität‘ und ‚Quantität‘. Die Rekonstruktion führt dennoch zu spannenden Themen, z.B. zu einem möglichen Einstieg in das weltverändernde Phänomen der kognitiven Evolution.

6. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 6 geht es um die Begriffe ‚Definition‘ und ‚Beschreibung‘. Im Verhältnis zwischen beiden Begriffen geht die Beschreibung der Definition voraus. In der ‚Definition‘, die Avicenna vorstellt, wird ein neuer Ausdruck e mittels anderer Ausdrücke <e1, …, ek>, die sich auf schon bekannte Sachverhalte beziehen, ‚erklärt‘. Die von Avicenna dann vorgenommene Erklärung, was eine ‚Definition‘ sei, hängt u.a. stark ab von dem Begriff der ‚Bekanntheit‘ und dem Begriff des ‚wahren Wesens‘. Für die Tatsache, dass ein Mensch A bestimmte Ausdrücke <e1, …, ek> einer Sprache L ‚kennt‘ oder ’nicht kennt‘, dafür gibt es keine allgemeinen Regeln oder Kriterien. Von daher macht die Verwendung der Ausdrücke ‚bekannt’/ ’nicht bekannt‘ eigentlich nur Sinn in solch einem lokalen Kontexten W* (z.B. einem Artikel, ein Buch, ein Vortrag, …), in dem entscheidbar ist, ob ein bestimmter Ausdruck e einer Sprache L schon mal vorkam oder nicht. Schwierig wird es mit dem Begriff des ‚wahren Wesens‘. In meiner Interpretation mit der dynamischen Objekthierarchie gibt es ‚das wahre Wesen‘ in Form von Objekten auf einer Stufe j, die Instanzen auf Stufen kleiner als j haben. Dazu gab es weitere Überlegungen.

7. Im folgenden Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 7 beschreibt Avicenna syntaktisch zusammengesetzte, aber semantisch einfache Ausdrücke. Innerhalb der Ausdrücke unterscheidet er die Teileausdrücke ‚Name‘, ‚Verb‘ und ‚Präposition‘. Die unterschiedliche Charakterisierung erfolgt nicht aufgrund der syntaktischen Form, sondern aufgrund der semantischen Eigenschaften, die mit diesen Ausdrücken verbunden werden. Neben dem Objektbezug, der die eigentliche Bedeutung fundiert, gibt es im Bedeutungsraum auch noch den zeitlichen und den räumlichen Aspekt. Das Zusammenspiel von Bedeutung und Ausdruck wird angerissen.

8. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 8 geht es um solche Ausdrücke E, die ‚Aussagen‘ P sind, von denen man sagt, dass sie ‚wahr‘ oder ‚falsch‘ seien. Aussagen sind eine echte Teilmenge aller Ausdrücke, $latex P \subset E$. Avicenna unterscheidet drei Arten von Aussagen: ‚kategorische‘ Aussagen, ‚Disjunktiv-konditionelle‘ und ‚Konjunktiv-konditionelle‘. Es wird ausführlich eine mögliche Wahrheitstheorie für die Zuschreibung ‚wahr’/ ‚falsch‘ diskutiert. Dann werden nochmals die Aussagetypen näher untersucht. Ein Zusammenhang mit der modernen Aussagenlogik wird hergestellt. Disjunktion, Konjunktion (und ergänzend) Implikation) sind Aussagetypen, die aus zwei Teilausdrücken A und B bestehen, die selbst wieder Aussagen sind, die wahr oder falsch sein können. Die beiden Teilausdrücke A und B werden dann durch die Teilausdrücke (oder), (und) sowie (wenn)-(dann)- verknüpft. Sie unterscheiden sich dadurch, wie der Wahrheitswert des Gesamtausdrucks von der Verteilung der Wahrheitswerte auf die Teilausdrücke festgelegt ist. Die Teilausdrücke (oder), (und) sowie (wenn)-(dann)- nennt man später dann auch ‚aussagenlogische Operatoren‘. Der Aussagetyp ‚kategorisierend‘ passt nicht in dieses Schema. Der Aussagetyp ‚kategorisierend‘ ist eine Aussage A, die wahr oder falsch sein kann unabhängig von irgendeinem aussagenlogischen Operator. Auch wird die Verneinung/ Negation diskutiert. Ausdrücke wie (Etwas)(ist nicht)(dies)(oder)(jenes) wurden rekonstruiert als $latex \neg(A)(oder)(B)$ mit dem Zeichen $latex \neg$ für ’nicht‘ oder ‚es ist nicht der Fall, dass‘.

9. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 9 kommt Avicenna auf mehrere Begriffspaare zu sprechen, die sich z.T. mit Themen berühren, die er schon vorher besprochen hat, z.T. neue Aspekte thematisieren, die nicht so ohne weiteres mit dem bisher Gesagten harmonieren. Es handelt sich z.B. um die Begriffe ‚Kategorisch‘, ‚Negation‘, ‚Universal‘, ‚Partikulär‘, die aber jetzt mit neuen Randbedingungen nochmals diskutiert werden. So stellt er die Frage, wann ‚kategorischen‘ (‚kategorisierenden‘) Aussagen ‚affirmativ‘ und wann sie ’negativ‘ sind. Ferner führt er neben den bisherigen die semantisch motivierten Begriffe ‚Name‘, ‚Verb‘ (auch ‚Term‘ genannt), sowie ‚Präposition‘ nun auch das Begriffspaar ‚Subjekt‘ und ‚Prädikat‘. Auch diese sind ’semantisch‘ motiviert, d.h. nur durch Rückgriff auf die Bedeutung kann man zur Klassifikation ‚Subjekt‘ bzw. ‚Prädikat‘ kommen. In den soeben erwähnten Kontexten wie auch in nachfolgenden Beispielen diskutiert Avicenna auch die Begriffe ‚affirmativ‘ und ’negativ‘. Zwischendrin bemerkt er auch mal, dass das Treffen einer Feststellung, eigentlich nur Sinne mache, wenn dasjenige, von dem etwas ausgesagt wird, auch existiere. Doch wird dieser Punkt nicht weiter diskutiert. Vom Subjekt einer Aussage sagt Avicenna, dass es partikulär‘ oder ‚universell‘ sein kann. Falls universell, dann kann man unterscheiden, ob sie ‚unbestimmt‘ (engl.: ‚indeterminate‘) ist – wie viele genau involviert sind — oder eben ‚bestimmt‘ (engl.: ‚determinate‘). Ferner illustriert er am Beispiel der kategorisierenden Aussagen auch die Begriffe ’notwendig‘ und ‚kontingent‘. Diese Verwendung der Begriffe stimmt überein mit den zuvor eingeführten Begriffe ‚wesentlich‘ und ‚akzidentell‘. Auch erwähnt Avicenna den Begriff ‚möglich‘. Er sieht mindestens zwei Verwendungsweisen von ‚möglich‘: In der Diskussion dieses Abschnitts werden einerseits einige Widersprüchlichkeiten in den Ausführungen Avicennas sichtbar gemacht, andererseits wird die Rekonstruktion einer möglichen systematischen Theorie zur Logik Avicennas fortgesetzt. Die wichtigsten Kritikpunkte kreisen um das Begriffspaar ‚affirmativ – negativ‘ mit der Kritik, dass beide Begriffe auf unterschiedlichen semantischen Ebenen liegen. Ferner widerspricht die Handhabung der Quantoren durch Avicenna der allgemeinen Verwendung.

10. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 10 diskutiert Avicenna seine Begriffe ‚Konjunktives‘ und ‚Disjunktives Konditional‘ unter verschiedensten Aspekten. Einige davon sind die Quantoren (wobei er auch Quantoren über die Zeit benutzt!), das Begriffspaar ‚Antezedenz – Konsequenz‘, der Begriff der ‚Harmonie‘, und wiederholt die Aspekte ‚Existenz‘, ‚Affirmation‘ sowie ‚Bestimmt/ Unbestimmt‘. Alle diese Aspekte werden in diesem Blogeintrag schon ein wenig ‚vorsortiert‘, um dann im nachfolgenden Blogeintrag weiter rekonstruierend diskutiert zu werden.

11. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 11 erfolgt eine ‚rekonstruierende Diskussion‘ von Avicennas Überlegungen aus Blogeintrag 10. Seine Überlegungen werden aufgegriffen und in einen theoretischen Rahmen eingeordnet, der es erlaubt, die Begriffe schärfer zu fassen und sie dadurch besser voneinander abzugrenzen. Nach einer Übersicht über die Struktur der Aussagen erfolgt dann eine Rekonstruktion von Bedeutungszuordnungen und eine Erklärung von Begriffen wie ‚wahr’/ ‚falsch‘, ‚Existenz‘, und ‚möglich‘.

12. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 12 diskutiert Avicenna den Fall widersprüchlicher Aussagen. Gemessen an dem bisher Gesagten bringt er in diesem Abschnitt keine neuen Aspekte ins Spiel. Wohl aber bietet dieser Abschnitt weitere Beispiele für sein Auffassung des Sachverhalts. Sie belegen, wie schwer er sich durchgängig damit tut, in dem unscharfen Wechselspiel von Ausdrucksseite und Bedeutungsseite eine konstante Verwendungsweise seiner Begriffe durchzuhalten. In diesem Blogeintrag erfolgt die Diskussion seines Textes immer unmittelbar hinter jedem Punkt in Form einer Anmerkung.

13. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 13 diskutiert Avicenna die Möglichkeit der Konvertierung von Aussagen mit Quantoren in solche, deren Bedeutung trotz Veränderung von Ausdruckselementen ‚erhalten‘ bleibt. In einigen Beispielen widerspricht er sich selbst; manche Stellen sind unklar. Es zeigt sich allgemein: (i) die Formulierung von Konvertierungsregeln greift beständig auf bestimmte unterstellte Bedeutungen zurück und (ii) genau diese unterstellten Bedeutungen werden nicht hinreichend klar definiert. Daraus entsteht die Forderung, diese unterstellte Bedeutung klar zu definieren und auf dieser Basis alle logischen Ausdruckselemente eindeutig zu definieren (was im nachfolgenden Abschnitt dann unternommen wird).

14/14b. In den Blogeinträgen AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 14 sowie AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 14b geht es darum, erstmalig einen theoretischen Rahmen für eine Semantik zu formulieren, mit der man die Logik Avicennas konsistent entwickeln kann. Abschnitt 14b stellt eine Überarbeitung des Eingangsteils von Abschnitt 14 dar. Es hat sich gezeigt, dass die in 14b gewählte Begrifflichkeit für das weitere Vorgehen ‚günstiger‘ wirkt. Aber wir befinden uns noch in der Phase der ‚Annäherung‘ an das ‚Neue‘.

15. In dem Blogeintrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 15 geht es um die Feinstruktur von Aussagen. Avicenna unterteilt ja Ausdrücke anhand inhaltlicher Kriterien nach Subjekt S, Prädikat P und ergänzend nach Quantoren Q. Es fragt sich, wie man diesen Ausdrucksteilen eine ‚Bedeutung‘ im Objektraum O zuordnen kann. Wichtig ist hier die schon früher getroffene Unterscheidung zwischen ‚echten‘ und ‚unechten‘ Objekten. ‚Unechte‘ Objekte wurden als ‚Eigenschaften‘ bezeichnet. Mit dieser Terminologie kann man sagen, dass die Objekthierarchie O primär von echten Objekten gebildet wird; unechte Objekte als Eigenschaften treten nur im Kontext eines echten Objekts auf. Damit kann man die begriffe ‚Gattung‘ und ‚Art‘ einführen. Gattungen, die keine Gattungen mehr ‚über sich‘ haben können, sollen hier ‚Kategorien‘ genannt werden. Setz man Definitionen von Worten voraus, dann kann man ach erklären, warum eine Aussage wie ‚a ist eine Tasse‘ ‚rein definitorisch‘ (bzw. ‚rein analytisch‘) ‚wahr ist, unabhängig davon, ob diesem gedanklichen Sachverhalt etwas Sinnliches entspricht. Im Gegensatz zu solch einer rein definitorischen (analytischen) Wahrheit eines Objekts a soll hier die ursprünglich vereinbarte ‚Wahrheit‘ durch Bezug auf eine ’sinnliche Gegebenheit‘ $latex s \subseteq Os$ ‚ontologische‘ Wahrheit genannt werden. Solange wir uns in unseren Aussagen auf das Enthaltensein eines Objektes a in einem Gattungsobjekts X beschränken ‚a ist ein X‘ oder das Feststellen von Eigenschaften der Art ‚a hat b‘ kann man sagen, dass eine Aussagestruktur wie (S P) wie folgt interpretiert werden kann: Es gibt einen Ausdruck A=(AsAp), bei dem ein Ausdrucksteil As sich auf ein echtes Objekt M(As) = $latex a \in Oa$ bezieht und der andere Ausdrucksteil Ap bezieht sich auf die Beziehung zwischen dem Objekt a und entweder einem Gattungsobjekt X (Ap = ‚ist ein X‘) oder auf eine Eigenschaft Y (Ap = ‚hat Y‘). Hierbei ist eine gewisse ‚Asymmetrie‘ zu beachten. Die Bedeutung vom Ausdrucksteil As – M(As) – bezieht sich auf eine ‚konkrete‘ Eigenschaftsstruktur innerhalb der Objekthierarchie. Die Bedeutung vom Ausdrucksteil Ap – M(Ap) – bezieht sich auf eine ‚Beziehung‘ / ‚Relation’/ ein ‚Verhältnis‘ [R] zwischen dem bezeichneten Bedeutungsobjekt M(As) = a und einem anderen bezeichneten Bedeutungsobjekt M(Ap), also R(M(As), M(Ap)). Die Beziehung R ist selbst kein ‚Objekt‘ so wie das Objekt a oder das implizit angenommene ‚Bezugsobjekt‘ X bzw. Y von a. Eine solche Beziehung R setzt – um prozessural ‚hantierbar‘ zu sein – eine zusätzliche ‚Objektebene‘ voraus, auf der es ein R-Objekt gibt, das die Beziehung zwischen dem a-Objekt und dem X-Y-Objekt ‚repräsentiert.

16. In dem Blogeintrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 16 wird die Analyse der vorausgesetzten Objekthierarchie O und der damit interagierenden Ausdrucksstruktur E weiter analysiert. Nach der Analyse der Feinstruktur von (S P) werden die Aspekte Anzahl, Raum und Zeit betrachtet. Es wird gezeigt, wie man für diese Aspekte sowohl ‚globale Quantoren‘ wie auch ‚lokale Relationen‘ einführen kann; zudem ist die Wechselwirkung zwischen diesen Aspekten konfliktfrei, da sie voneinander unabhängig sind.

17. In dem Blogeintrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 17 geht es um die Frage, wie man Aussagen über Veränderungen in der hypothetisch angenmmenen Bedeutungsstruktur nachzeichnen kann. Es lässt sich erkennen, dass die Kodierung von Veränderungen mittels Ausdruckselementen innerhalb eines Prädikates P mittels ‚Veränderungsausdrücken‘ V (‚Verben‘) oft nicht nur die beteiligten Objekte Y benennt, sondern zusätzlich zahlreiche weitere Ausdruckselemente aktiviert, die räumliche Gegebenheiten R_r bezeichnen, zeitliche Relationen R_t, zusätzliche Eigenschaften At an den Veränderungen; dazu ferner spezielle kulturelle Relationen R_x einbeziehen können sowie mit zusätzlichen Subjektrepräsentationen operieren. Auch kann man beobachten, wie die Aneinanderreihung von unterschiedlichen Sachverhalten (S P) mit logischen Operatoren (S P) UND (S2 P2) auch zu speziellen Verkürzungen führen kann wie (S P1 UND P2). Dies lässt erahnen, dass eine vollständige Analyse auch nur einer einzigen Alltagssprache von ihrer logisch relevanten Semantik her eine schier unendliche Aufgabe ist. Diese wird weder ein einzelner Mensch alleine noch viele Menschen über viele Genrationen hinweg jemals vollständig erfüllen können. Was aber möglich erscheint, das ist die Analyse des grundlegenden Mechanismus, der sich mit Hilfe von evolvierenden Computermodellen experimentell untersuchen und mit realen semiotischen Systemen überprüfen lässt.

18. In dem Blogeintrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 18 weitet sich nun der Blick Avicennas auf das Wissen allgemein, und konzentriert sich im Wissen auf das schlussfolgernde Denken in Form von ‚beweisenden Syllogismen‘. Nach einer Definition von ‚Syllogismus‘ unterscheidet er dann zwei Arten von Syllogismen ‚Konjunktiver‘ Syllogismen und ‚Disjunktiver‘ Syllogismus. Am Beispiel des ‚Konjunktiven Syllogismus‘ führt Avicenna dann eine Reihe von technischen Begriffen ein. Dann stellt Avicenna zusätzliche Beschränkungen vor, um die 256 möglichen Figuren/ Muster auf nur 27 mögliche Muster einzuschränken. Alle seine Festlegungen geschehen ohne eigentliche Begründung.

19. In dem Blogeintrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 19 beginnt die Diskussion um die Interpretation der syllogistischen Schlussfiguren am Beispiel der ersten Figur (A F B), (A B H) und (A F H) mit der Quantorenbelegung ‚AAA‘. In einzelnen Schritten wird dann eine erste Skizze zu einer Logik auf der Basis einer dynamischen Objektstruktur erarbeitet. Zentrale Begriffe sind hier OBJEKTIFIZIERUNG, ENTHALTENSEIN, ZUSCHREIBUNG und VERERBUNG. In dieser Skizze werden auch ‚Aktivitäten‘ berücksichtigt, die in dem Muster zur ersten Figur nicht vorkommen, zusätzlich werden neben den Anzahlquantoren auch Raum- und Zeitquantoren berücksichtigt.

20. In dem Blogeintrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 20 geht es um die Interpretation des zweiten Musters der ersten syllogistischen Schlussfigur ‚A F ist B‘, ‚A B ist nicht H‘ (als ‚Kein A ist B‘), ‚A F ist nicht H‘ (als ‚Kein F ist H‘), dazu die Beispiele ‚Jeder ausgedehnte Körper ist farbig‘, ‚Kein farbiger Körper ist unerschaffen‘, ‚Kein ausgedehnter Körper ist unerschaffen‘. Wir treffen in diesem Muster wieder auf den Prozess der Objektifizierung, tatsächlich sogar in impliziten Formen mit der expliziten Angabe von Eigenschaften und der stillschweigenden Annahme einer daraus sich ergebenden Mengenbildung. Zusätzlich finden sich wieder Enthaltensbeziehungen einerseits anhand von Eigenschaftszuschreibungen, andererseits durch Benutzung von Anzahlquantoren. Die Zuschreibung von Eigenschaften wird explizit vorgenommen. Eine Vererbung von Eigenschaften von einer Menge zur anderen tritt nur implizit über eine Enthaltensbeziehung auf. Es tritt nur eine Sorte von Quantoren auf. Auch sei angemerkt, dass außer der Negation kein weiterer aussagenlogischer Operator auftritt.

21. In dem Blogeintrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 21 geht es um die Interpretation der Muster 3-4 der Schlussfigur 1. Dabei entsteht die Vermutung, dass viele der Unterscheidungen von Avicenna (die weitgehend auf Aristoteles zurückgehen!) möglicherweise ‚redundant‘ sind, d.h. mit anderen Formulierungen letztlich doch ‚das Gleiche‘ sagen. Der Ansatzpunkt für diese Vermutung liegt darin begründet, dass die Unterscheidung von einem Term als ‚Subjekt‘ (S) und als ‚Prädikat‘ (P) auf Seiten der abstrakten Bedeutungsstruktur als Bedeutungsrepräsentation jeweils ein ‚echtes‘ oder ein ‚unechtes‘ Objekt haben können, und zwar so, dass diese Strukturen ‚fließend‘ sind: jedes ‚echte‘ Objekt kann als ‚unechtes‘ interpretiert werden und umgekehrt. Weitere Vereinfachungen deuten sich an. Diese sollen im Folgenden überprüft werden.

Fortsetzung folgt …

QUELLEN

  • Avicenna, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
  • Digital Averroes Research Environment
  • Immanuel Kant, Critik der reinen Vernunft‘, Riga, 1781
  • Konrad Lorenz, 1973, ‚Die Rückseite des Spiegels. Versuch einer Naturgeschichte des menschlichen Erkennens‘, München, Zürich: Piper
  • Günther Patzig, ‚Die Aristotelische Syllogistik‘, 3,verb.Aufl., Göttingen: Vandenhoeck & Rupprecht, 1969
  • Nicholas Rescher (1928 – ),The Development of Arabic Logic. University of Pittsburgh Press, 1964
  • Hans-Jörg Sandkühler (Hg.) unter Mitwirkung von Dagmar Borchers, Arnim Regenbogen, Volker Schürmann und Pirmin Stekeler-Weithofer, ‚Enzyklopädie Philosophie‘, 3 Bd., Hamburg: FELIX MEINER VERLAG, 2010 (mit CD-ROM)
  • Stanford Encyclopedia of Philosophy, Aristotle’s Logic
  • Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7

Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER.

AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 9

Affirmativ, Ausdruck, Ausdruck - einfacher, Ausdruck - sprachlicher, Ausdruck - zusammengesetzter, Aussage, Aussagetypen, Avicenna, Kategorisch, kontingent, Logik, Logik - Alltag, Logik - Antike, Logik - formale, Möglichkeit, Negation, Notwendig, Partikulär, Prädikat, Quantität, Quantor, Subjekt, universal, universell

(Mit Nachtrag vom 1.Sept.2014)

VORGESCHICHTE

Für einen Überblick zu allen vorausgehenden Beiträgen dieser rekonstruierenden Lektüre von Avicennas Beitrag zur Logik siehe AVICENNAS ABHANDLUNG ZUR LOGIK – BLITZÜBERSICHT.

Nach der üblichen Darstellung der Position von Avicenna folgt dann der Teil ‚DISKUSSION‘, in der seine Position kritisch hinterfragt und die Rekonstruktion einer möglichen Theorie der Alltagslogik fortgesetzt wird.

KATEGORISCH – AFFIRMATIV/ NEGATION – UNIVERSAL/ PARTIKULÄR

1. Im folgenden Abschnitt treten Begriffe auf, die z.T. schon zuvor auftraten (‚Kategorisch‘, ‚Negation‘, ‚Universal‘, ‚Partikulär‘), die aber jetzt mit neuen Randbedingungen nochmals diskutiert werden.

KATEGORISCH ALS AFFIRMATIV/ NEGATIV

2. Der Abschnitt beginnt mit einer Diskussion von ‚kategorischen‘ (‚kategorisierenden‘) Aussagen und der Frage, wann sie ‚affirmativ‘ und wann sie ’negativ‘ sind.

SUBJEKT – PRÄDIKAT, EINFACH – ZUSAMMENGESETZT

3. Zusätzlich zu den Unterscheidungen ‚affirmativ‘ – ’negativ‘ im Kontext einer ‚kategorisierenden‘ Aussage berücksichtigt Avicenna auch hier wieder Teilausdrücke. Während er zuvor die semantisch motivierten Begriffe ‚Name‘, ‚Verb‘ (auch ‚Term‘ genannt), sowie ‚Präposition‘ erwähnt hatte, benutzt er nun auch das Begriffspaar ‚Subjekt‘ und ‚Prädikat‘. Beide sind – wie sich aus dem Verwendungskontext nahelegt – ’semantisch‘ motiviert, d.h. nur durch Rückgriff auf die Bedeutung kann man zur Klassifikation ‚Subjekt‘ bzw. ‚Prädikat‘ kommen.
4. Versucht man die Begriffe ‚Name‘, ‚Verb‘ (‚Term‘), sowie ‚Präposition‘ mit den neuen Begriffen ‚Subjekt‘ und ‚Prädikat‘ in Beziehung zu setzen, dann gibt es eine gewisse Korrelation zwischen ‚Name‘ und ‚Subjekt‘ einerseits sowie ‚Verb‘ und ‚Prädikat‘ andererseits. Da Avicenna selbst keinerlei weitere Hinweise auf eine mögliche Beziehung liefert, bleibt an dieser Stelle einiges unklar.
5. Deutlich ist nur, dass Avicenna die Ausdrucksseite eines Ausdrucks e = <e1, e2, …> durch Rückgriff auf eine – nicht explizit beschriebene – Bedeutungsstruktur so analysiert, dass er sagen kann, welche ‚Teile‘ des Ausdrucks e als ‚Subjekt‘ zu nehmen sind, und welche Teile als ‚Prädikat‘.
6. So unterscheidet er im Bedeutungsraum zwischen ‚dem, über das‘ eine Feststellung getroffen wird, und ‚dem, was‘ in dieser Feststellung gesagt wird.
7. Im Beispielsatz N:(der Mensch)V:(ist)N:(ein Lebewesen) analysiert er den Teil [N:(der Mensch)] als ‚Subjekt‘ und den Teil [V:(ist)N:(ein Lebewesen)] als ‚Prädikat‘.
8. Ein anderer Beispielsatz (Wer immer)(sein)N:(Essen)OP:(nicht)V:(kaut)(der)V:(schädigt)(seinen)N:(Darm) enthält Aussageteile, für die Avicenna bislang keine semantisch motivierte grammatische Beschreibungskategorien eingeführt hat. Avicenna analysiert den Ausdruck wie folgt: Subjekt = [(Wer immer)(sein)N:(Essen)OP:(nicht)V:(kaut)] und Prädikat = [(der)V:(schädigt)(seinen)N:(Darm)].
9. Den Unterschied zwischen Subjekt = [N:(der Mensch)] und Subjekt = [(Wer immer)(sein)N:(Essen)OP:(nicht)V:(kaut)] charakterisiert Avicenna als Unterschied zwischen einem ‚einfachen‘ und einem ‚zusammengesetzten‘ Subjekt. Entsprechend auch für das Prädikat: Prädikat = [V:(ist)N:(ein Lebewesen)] und Prädikat = [(der)V:(schädigt)(seinen)N:(Darm)].
10. Sowohl für die Verwendung der Begriffe ‚Subjekt/ Prädikat‘ wie auch ‚einfach/ zusammengesetzt‘ liefert Avicenna keine explizite Kriterien. Er zitiert nur einige Ausdrücke als Beispiele und appelliert an die sprachliche Intuition des Lesers, die implizit verwendeten Analysekriterien zu verstehen.

AFFIRMATIV – NEGATIV

11. In den soeben erwähnten Kontexten wie auch in nachfolgenden Beispielen diskutiert er auch die Begriffe ‚affirmativ‘ und ’negativ‘.
12. Sein Hauptkriterium zur Verwendung der Begriffe ‚affirmativ‘ und ’negativ‘ ist der (semantische, bedeutungsgeleitete!) Aspekt, ob das, was in einer Aussage in einem Prädikat von einem Subjekt behauptet wird, ‚zutrifft’/ ‚der Fall ist‘ oder ’nicht zutrifft’/ ’nicht der Fall ist‘. Trifft das im Prädikat behauptete zu, dann will er es ‚affirmativ‘ nennen, ansonsten ’negativ‘.
13. Im vorausgehenden Abschnitt waren diese Verwendungskriterien auch benutzt worden, um zu sagen, wann eine Aussage ‚wahr‘ bzw. ‚falsch‘ ist. Nach den bisherigen Kriterien müsste man dann sagen, dass ‚wahr‘ und ‚affirmativ‘ einerseits und ‚falsch‘ und ’negativ‘ dann bedeutungsgleich wären.
14. In einem weiteren Beispiel benutzt Avicenna die Aussage SUBJ[N:(Zid)] PRÄD[V:(ist)(ohne)N:(Sicht)] – engl.: ‚Zid is without sight‘ – als ein Beispiel für eine ‚affirmative‘ Aussage, da das Prädikat PRÄD[V:(ist)(ohne)N:(Sicht)] eine Eigenschaft beschreibt, die auf das Subjekt (Zid) zutrifft.
15. Andererseits wird der Teilausdruck ‚ist ohne Sicht‘ bedeutungsmäßig als eine ‚Negation‘ verstanden im Sinne von ‚hat keine Sicht‘ im Gegensatz zu ‚hat Sicht‘. D.h. eine bedeutungsmäßige ‚Verneinung‘ kann durch verschiedene Ausdruckselemente realisiert werden, auch ohne den Ausdruck ’nicht‘. Dies würde bedeuten, dass eine ‚ausdrucksmäßig realisierte Verneinung‘ das Fehlen einer bestimmten Eigenschaft aussagen kann. Nach den Worten Avicennas kann aber genau solche eine Feststellung, dass eine bestimmte Eigenschaft fehlt, eine ‚Affirmation‘ sein, eben das Festellen, dass es der Fall ist, dass eine bestimmte Eigenschaft fehlt.
16. Wenn also eine Affirmation das Absprechen einer Eigenschaft beinhalten kann, wie sieht dann eine Verneinung einer solchen Affirmation aus?
17. Avicenna bringt folgendes Beispiel: SUBJ[N:(Zid)] PRÄD[V:(ist)(nicht)(ohne)N:(Sicht)]. Für ihn ist dieses eine ‚Negation‘, da die Affirmation, eine bestimmte Eigenschaft sei nicht da, verneint wird.
18. Mann könnte das Beispiel auch umschreiben zu: (Es ist nicht der Fall, dass) SUBJ[N:(Zid)] PRÄD[V:(ist)(ohne)N:(Sicht)].
19. Ersetzt man die Teilausdrücke durch Buchstaben – was Avicenna im Text auch einmal demonstriert –, dann könnte man auch schreiben (Es ist nicht der Fall, dass) (A)(B), bzw. dann $latex (A)\neg(B)$.

EXISTENZ

20. Zwischendrin bemerkt Avicenna auch mal, dass das Treffen einer Feststellung, eigentlich nur Sinn mache, wenn dasjenige, von dem etwas ausgesagt wird, auch existiere. Doch wird dieser Punkt nicht weiter diskutiert.

UNIVERSELL – PARTIKULÄR – QUANTITÄT – QUANTOREN

21. Vom Subjekt einer Aussage sagt Avicenna, sie kann ‚partikulär‘ oder ‚universell‘ sein. Falls universell, dann kann man unterscheiden, ob sie ‚unbestimmt‘ (engl.: ‚indeterminate‘) ist – wie viele genau involviert sind — oder eben ‚bestimmt‘ (engl.: ‚determinate‘).
22. Im Beispielausdruck (Zid)(ist)(ein)(Lebewesen) ist (Zid) ‚partikulär‘.
23. Im Beispielausdruck (Menschen)(bewegen)(sich) ist nach Avicenna unklar, ob ‚alle‘ Menschen gemeint sind oder nur ‚einige‘.
24. Die ‚bestimmten universellen Aussagen‘ teilt Avicenna in vier Klassen ein:
25. Typ 1: Subjekt = Alle, Affirmativ (Bsp.: Q=[(Jeder)]S=[(Mensch)]P=[(ist)(ein)(Lebewesen)]
26. Typ 2: Subjekt = Alle, Negativ (Bsp.: Q=[(Kein)]S=[(Mensch)]P=[(ist)(sterblich)](?)
27. Typ 3: Subjekt = Einige, Affirmativ Q=[(Einige)]S=[(Mensch)]P=[(sind)(Schriftsteller)]
28. Typ 4: Subjekt = Einige, Negativ Q=[(Nicht alle)]S=[(Mensch)]P=[(sind)(Schriftsteller)] (?)
29. Hier sind nur einige von Avicennas Beispielsätzen angeführt. Einige Beispiele werfen Fragen auf (?).
30. Mehrfach formuliert Avicenna auch folgendes ‚Metaprinzip‘: Wenn eine Aussage über ‚Alle‘ spricht, dann sei es unsicher, ob wirklich alle gemeint sind; sicher sei es aber, dass wenigstens ‚einige‘ gemeint sind.
31. Aus all diesen Überlegungen leitet er dann folgende Fallunterscheidungen her (von mir abgekürzt ‚+‘ für ‚affirmativ‘, ‚-‚ für negativ‘, ‚1‘ für ‚partikulär‘, ‚0‘ für ‚unbestimmt‘ und ‚a‘ für universell‘:
32. (+,1)
33. (-,1)
34. (0,+)
35. (0,-)
36. (a,+)
37. (a,-)
38. (1,+)
39. (1,-)
40. Die Fälle (+,1) und (-,1) bezeichnet Avicenna als ’nutzlos für die Wissenschaft‘ und die Fälle (0,+) und (0,-) sollten vermieden werden, da sie ‚verwirrend‘ sind.

NOTWENDIG – KONTINGENT

41. Am Beispiel der kategorisierenden Aussagen illustriert Avicenna auch die Begriffe ’notwendig‘ und ‚kontingent‘. Die Verwendung dieser Begriffe stimmt überein mit den zuvor eingeführten Begriffe ‚wesentlich‘ und ‚akzidentell‘.

MÖGLICH

42. Auch erwähnt Avicenna hier den Begriff ‚möglich‘. Er sieht mindestens zwei Verwendungsweisen von ‚möglich‘: einmal als (i) ’nicht unmöglich‘ und (ii) im Sinne von ‚kann existieren‘ und ‚kann nicht existieren‘. Fall (ii) ist für ihn das ‚real mögliche‘ und stimmt nach Ihm mit dem normalsprachlichen Gebrauch überein.
43. Die Verwendungsweise in Fall (i) von ‚möglich := nicht unmöglich‘ widerspricht eigentlich den Regel einer expliziten Definition, wie er sie an früherer Stelle aufgestellt hatte. Dort hatte er verlangt, dass der neu zu definierende Ausdruck e_new nicht auf der rechten Seite bei den definierenden – als bekannt vorausgesetzten – Ausdrücken vorkommen darf, also e_neu := <e_alt1, …, e_altn>.
44. Der Ausdruck ‚möglich := nicht unmöglich‘ entspricht dem Ausdruck ‚möglich := nicht nicht möglich‘. Darin wird der neue Ausdruck über sich selbst definiert, was ‚zirkulär‘ ist.

DISKUSSION

45. Dieser neue Text verstärkt den Eindruck der vorausgehenden Seiten, dass Avicenna keine wirklich systematische Theorie hat. Er folgt den in der Literatur vorkommenden Begriffen nach keiner erkennbaren Regel, und seine Analyse benutzt Kriterien, die höchst selten explizit benannt werden. Vorzugsweise stellt er Beispielsätze vor, die er nach impliziten Kriterien diskutiert. Auch wiederholt er scheinbar ähnliche Bedeutungszusammenhänge mit jeweils neuen Begriffen. Dennoch besteht noch immer der Eindruck, dass sich der bislang gewählte Interpretationszusammenhang durchhalten lässt.

REKONSTRUIERENDE ECKWERTE BISHER

46. Als Eckwerte der rekonstruierenden Interpretation gilt bislang die Unterscheidung vom (i) ‚wissenden System‘ S in einer (ii) umgebenden realen Welt W und der Fähigkeit des wissenden Systems, (iii) bestimmte Ereignisse X der realen Welt W über einen Verarbeitungsprozess $latex \lambda$ in einen (iv) internen Bedeutungsraum M zu übersetzen. Parallel zum Bedeutungsraum M gibt es (v) eine Menge von Ausdrücken E, die (vi) auf unterschiedliche Weise mit dem Bedeutungsraum E innerhalb einer gewussten Beziehung $latex K \subseteq E \times M$ verknüpft werden können. Im Bereich des Bedeutungsraumes M kann (vii) unterschieden werden zwischen ‚aktuellen‘ Bedeutungsrepräsentationen M_now, die von aktuellen Ereignissen X der realen Welt verursacht sind, und ‚zeitlosen‘ Bedeutungsrepräsentationen M_0, mit $latex M_{now} \cap M_{0} = \emptyset, M_{now} \subseteq M, M_{0} \subseteq M$. Der Unterschied zwischen $latex M_{now}, M_{0}$ bezieht sich auf die zeitliche Komponente T in $latex M_{now}, M_{0}$. Würde man die zeitliche Komponente T aus $latex M_{now}$ ‚herausrechnen (also etwa $latex M_{now0} = M_{now} – T$), dann könnten die beiden Mengen $latex M_{now}, M_{0}$ gemeinsame Elemente enthalten ($latex M_{now0} \cap M_{0} \neq \emptyset$ ). Dies bedeutet, dass die charakterisierenden Eigenschaften der Objekte in $latex M_{now*}, M_{0}$ wissensmäßig ‚gleich‘ sein können. Durch (viii) Vergleich von Elementen aus M_now0 und M_0 kann dann entschieden werden, ob es der Fall ist, dass Elemente aus M_0 in M_now vorkommen oder nicht; falls sie vorkommen, dann ist eine feststellende (affirmative oder negative) Aussage ‚wahr‘, ansonsten ‚falsch‘.

REKONSTRUKTION: AFFIRMATIV – NEGATIV

47. Schon bei den von Avicenna angeführten Beispielen und deren Diskussion wird deutlich, dass eine gewisse Unklarheit darüber existiert, wie ’negative Ausdruckselemente‘ (wie z.B. ’nicht‘, ‚ohne‘) innerhalb des Begriffspaares ‚affirmativ/ negativ‘ zu bewerten sind. Zwar macht Avicenna darauf aufmerksam, dass das ‚Fehlen von etwas‘ eine Eigenschaft sein kann, die man ja gerade – affirmativ — aussagen möchte, aber es fehlt letztlich ein hartes Kriterium, wann das ‚Fehlen‘ von etwas nur ein ‚Ausdruckselement‘ ist oder ein ’semantischer Tatbestand‘, der ‚oberhalb‘ der Ausdruckselemente liegt, also wo es gerade das ‚Fehlen von etwas‘ ist, das man aussagen will.
48. In dieser Rekonstruktion wird davon ausgegangen, dass jede Aussage – entsprechend den Aussagen von Avicenna – entweder ‚wahr‘ oder ‚falsch‘ ist. Dies setzt voraus, dass jede Aussage als solche ‚grundsätzlich affirmativ‘ ist, sie will etwas über ein Subjekt aussagen. Für diese Aussage wird ein Ausdruck e generiert (in der Regel mit mehreren Teilausdrücken, mindestens Subjekt und Prädikat), der einen Sachverhalt m_p mittels des Prädikats über ein Subjekt m_s behauptet. Innerhalb der Aussage e kann der Sachverhalt m_p sowohl ‚zusprechend‘ (affirmativ) im Sinne von ‚ist ein…’/ ‚hat …‘ sein oder absprechend, negierend ‚ist nicht …‘, ‚hat nicht …‘ usw. Unabhängig davon ob die kombinierten Sachverhalte (m_s, m_p) ‚zusprechend‘ oder ‚absprechend‘ sind, können sie ‚wahr‘ (in der realen Welt W zutreffend) oder ‚falsch‘ (in der realen Welt W nicht zutreffend) sein.
49. Während die Frage von ‚wahr’/ ‚falsch‘ eine rein semantische Angelegenheit ist, die durch die simultane wissensmäßige Unterscheidung von ’nur gewusst/ gedacht/ vorgestellt/ erinnert/ im Sinne von $latex M_{0}$ einerseits und ‚als aktuell wahrgenommen gewusst‘ im Sinne von $latex M_{now}$ möglich ist, hängt die Unterscheidung von ‚affirmativ/ negativ‘ davon ab, ob es Ausdruckselemente gibt, die explizit so vereinbart sind, dass sie in einem S-P-Urteilszusammenhang als ‚zusprechend‘ oder ‚absprechend‘ identifiziert werden können. Wenn niemand weiß, dass ’nicht‘ in der Deutschen Sprache eine ‚Verneinung‘ darstellt, kann auch kein ‚Absprechen von etwas‘ erkennen. Wenn jemand aber weiß, dass mit dem Ausdruckselement ’nicht‘ etwas verneint wird, dann weiß er aufgrund der Aussagensemantik, dass der Ausdruck ‚ist nicht sterblich‘ eben die Verneinung von ‚ist sterblich‘ ist (unabhängig von ‚wahr‘ und ‚falsch‘). Und da die Bedeutung der Verneinung an den Ausdruck ’nicht‘ geknüpft ist, wird diese Bedeutung jedes mal aktiviert, wenn das Ausdruckselement ’nicht‘ auftritt: ‚ist nicht sterblich‘, ‚ist nicht nicht sterblich‘, ‚es gilt nicht, dass Zid nicht unsterblich ist‘, usw. Allerdings sind die Konventionen in jeder Sprache unterschiedlich, wie das Auftreten von negierenden Ausdruckselementen vorzunehmen ist (während im Deutschen eine Häufung wie ’nicht nicht‘ in Grenzfällen noch gehen mag, geht ’nicht nicht nicht‘ normalerweise nicht mehr. Darüber hinaus gibt es zahllose andere Ausdruckselemente (wie z.B. ‚kein(e), mit, ohne, haben, …), die auch negierende Funktionen übernehmen können.
50. Ein Ausdruck wie (Zid (ist ohne Sicht)), bedeutungsmäßig äquivalent etwa zu zu (Zid (hat keine Sicht)) oder (Zid (kann nicht sehen)), sagt affirmativ ein Fehlen aus. Ob dies während der Aussage in der realen Welt zutrifft (= wahr) oder nicht (=falsch), folgt aus der Aussage selbst nicht.
51. Eine Verneinung dieser Aussagen geschieht zunächst auf der Ausdrucksebene, und dann kann man den so konstruierten Sachverhalt bzgl. Wahrheit oder Falschheit bewerten.
52. Es hängt von geltenden Konventionen ab, wie man die Verneinung der Aussage (Zid (ist ohne Sicht)) auf der Ausdrucksebene realisiert. Eine Möglichkeit besteht darin, auf einer Metaebene zu sagen, ‚Die Aussage (Zid (ist ohne Sicht)) trifft nicht zu. Dies würde primär aber meinen, dass diese Aussage in der realen Welt W nicht zutrifft. Würde man die interne Struktur der Aussage (Zid (ist ohne Sicht)) ändern, dann würde man eine neue Aussage schaffen, von der man wiederum fragen kann, ob sie in der realen Welt W zutrifft oder nicht. Also man könnte natürlich formulieren (Zid (ist nicht ohne Sicht)); damit würde man verneinen, dass Zid ohne Sicht sei, also eine Verneinung der vorhergehenden Aussage. Aber auch diese neuerliche Verneinung wäre grundsätzlich eine Affirmation, nämlich etwas, was man über Zid Aussagen will.
53. Die rekonstruierende Hypothese lautet also: jeder Ausdruck e vom Typ Aussage PROP impliziert die Affirmation eines Sachverhaltes m_p über ein Subjekt m_s unabhängig davon, wie viele Negationen/ Verneinungen der Ausdruck e enthält. Eine so realisierte affirmative Aussage zu (m_s, m_p) kann wahr oder falsch sein.

EXISTENZ

54. Das von Avicenna nur kursorisch erwähnte Moment der Existenz ist in der aktuell rekonstruierenden Interpretation gegeben durch die Annahme der umgebenden realen Welt W, deren aktuelle induzierten Bedeutungsrepräsentationen M_now als Bezugspunkt für die Charakterisierungen wahr/ falsch genutzt werden kann. In diesem Rahmen können beliebige Aussagen gebildet werden ,unabhängig davon, ob sie aktuell wahr/ falsch sind.

MÖGLICH

55. Die Kategorie ‚möglich‘ ist durch die bloße Angabe ‚kann existieren und kann nicht existieren‘ kaum erklärt. Zu sagen, dass ein B über ein gegebenes/ bekanntes A ‚hinausgeht‘, setzt eigentlich voraus, dass man die Ereignisse X der realen Welt W zunächst mal überhaupt als ‚exstierend‘ erkennen kann $latex \lambda(X)$ , so dass dann relativ zu diesem Wissen $latex \lambda(X)$ ein anderes Element Y als ’neu‘ oder als ‚möglich‘ explizit gedacht werden könnte. Wir wissen vom menschlichen Denken, dass wir uns allerlei Dinge als M_0 ‚vorstellen‘, ‚denken‘, ‚träumen‘ … können, von denen zum Zeitpunkt des Vorstellens nicht bekannt ist, ob sie sich genauso auch ereignen werden. Bei einigen dieser Vorstellungen M_0* haben wir ein zusätzliches Wissen K*, aufgrund dessen wir aus der Vergangenheit wissen, dass sie mit einer gewissen Wahrscheinlichkeit eintreten können; von daher räumen wir diesen mittels K* als ‚eintretbar‘ klassifizierten Vorstellungen M_0* eine gewisse Möglichkeit ein. Bei anderen Vorstellungen $latex M_{X} = M_{0} – M_{0*}$ ist es uns weniger bis gar nicht klar, ob sie eintreten können, da das zugehörige Wissen K_X zu schwach ist.

QUNATITÄT – QUANTOREN

56. Im Kontext der schon zuvor erwähnten Begriffe ‚universell‘ und ‚partikulär‘ führt Avicenna nun den Gedanken der ‚Bestimmtheit’/ ‚Unbestimmtheit‘ ein und entwickelt daraus die Idee der Quantität in Gestalt von Quantoren.
57. Dies führt zu der grundsätzlichen Erweiterung (Q,S,P), d.h. das Zutreffen eines Sachverhaltes m_p wird nicht mehr nur für ein Subjekt S allgemein behauptet, sondern das Objekt m_s, das bedeutungsmäßig ein Subjekt fundiert, wird bezüglich seiner Quantität Q weiter spezifiziert als ‚Alle/ Jeder‘, ‚Nicht Alle/Einige‘, ‚Alle – nicht/ Keine(r)‘.
58. Bei der konkreten Angabe der sich daraus ergebenden möglichen Klassen kommt es aber dann bei Avicenna zu Unklarheiten, da er bei dieser Einteilung sein Begriffspaar ‚affirmativ/ negativ‘ benutzt, von dem wir zuvor gesehen haben, dass es möglicherweise ‚fehlerhaft‘ ist, da er den Begriff ‚affirmativ‘ und ’negativ‘ auf die gleiche semantische Stufe stellt. Wie zuvor aber schon festgestellt worden ist, muss man diese beiden Begriffe trennen. Wenn Avicenna z.B. die beiden ersten Typen seiner Aussagen klassifiziert als
59. Typ 1: Subjekt = Alle, Affirmativ (Bsp.: Q=[(Jeder)]S=[(Mensch)]P=[(ist)(ein)(Lebewesen)] oder Q=[(Jeder)]S=[(Mensch)]P=[(ist)(sterblich)]
60. Typ 2: Subjekt = Alle, Negativ (Bsp.: Q=[(Kein)]S=[(Mensch)]P=[(ist)(sterblich)](?)
61. dann ist die Charakterisierung von Typ 1 nachvollziehbar, von Typ 2 aber nicht. Von der Idee her soll in Typ 2 gezeigt werden, wie die Negation von Typ 1 beschaffen ist. In Typ 1 wird (affirmativ) behauptet, dass jeder Mensch ein Lebewesen ist bzw. sterblich ist. Im Typ 2 soll auch etwas (affirmativ) behauptet werden, nämlich dass ’nicht alle‘ Menschen Lebewesen sind bzw. sterblich sind. D.h. die Aussagen vom Typ 2 sind grundsätzlich weiterhin ‚affirmativ‘, es wird aber in ihrem Ausdruck ein zusätzliches verneinendes Ausdruckselement – hier ’nicht‘ – eingeführt, so dass der Sachverhalt, der affirmativ behauptet werden soll, ein zusätzliches verneinendes Element enthält. Daraus würde sich ergeben:
62. Typ 2b Q=[(Nicht alle)]S=[(Menschen)]P=[(sind)(sterblich)], was man umformen könnte zu Q=[(Einige)]S=[(Menschen)]P=[(sind)(nicht)(sterblich)].
63. Aus (nicht alle) folgt nicht (keine), wie bei Avicenna, sondern (einige).
64. Auch im Beispiel der Verneinung von ‚einige‘ kommt es bei Avicenna zu Unklarheiten:
65. Typ 3: Subjekt = Einige, Affirmativ Q=[(Einige)]S=[(Mensch)]P=[(sind)(Schriftsteller)]
66. Typ 4: Subjekt = Einige, Negativ Q=[(Nicht alle)]S=[(Mensch)]P=[(sind)(Schriftsteller)] (?)
67. Im Fall von Typ 4 geht es um die (affirmative) Behauptung, dass ’nicht einige‘ gemeint sind. Aus ’nicht einige‘ folgt aber nicht – wie bei Avicenna – ’nicht alle‘, sondern ‚(alle …. nicht…), d.h.
68. Typ 4b: Q=[(Nicht einige)]S=[(Mensch)]P=[(sind)(Schriftsteller)] kann umgeformt werden zu Q=[(Alle)]S=[(Mensch)]P=[(sind)(nicht)(Schriftsteller)]
69. Daraus folgt, dass eine Klassifikation nicht nach dem Muster (Q -affirmativ) und (Q – negativ) vorgenommen werden sollte, sondern nach dem Muster, alle Aussagen sind ‚affirmativ‘; innerhalb dieser Menge kann man verschiedene Quantoren unterscheiden (alle) bzw. (einige), und diese Quantoren sind entweder nicht verneint oder verneint. Das würde folgendes Schema ergeben:
70. Typ 1: Q=’alle‘
71. Typ 2b: Q='(nicht)(alle)‘ bzw. $latex (\neg)(Q)$ ist äquivalent zu Q=(einige),S,($latex \neg$),P).
72. Typ 3: Q=’einige‘
73. Typ 4b: Q='(nicht)(einige)‘ bzw. $latex (\neg)(Q)$ ist äquivalent zu Q=(alle),S,($latex \neg$),P).
74. Das von Avicenna formulierte ‚Metaprinzip‘: ‚Wenn eine Aussage über ‚Alle‘ spricht, dann ist es unsicher, ob wirklich alle gemeint sind; sicher ist es aber, dass wenigstens ‚einige‘ gemeint sind‘, muss auch hinterfragt werden. Würde sein Metaprinzip gelten, dann könnte man keine wirklichen ‚All-Aussagen‘ mehr machen, da grundsätzlich die intendierte Bedeutung von ‚alle‘ verneint würde. Dies macht keinen Sinn. Wenn jemand tatsächlich ‚alle‘ meint und dies ausdrücken will, dann muss der dazu vereinbarte Ausdruck ‚alle‘ auch entsprechend verwendet werden.
75. Die von Avicenna vorgenommene Fallunterscheidungen (von mir abgekürzt ‚+‘ für ‚affirmativ‘, ‚-‚ für negativ‘, ‚1‘ für ‚partikulär‘, ‚0‘ für ‚unbestimmt‘ und ‚a‘ für universell‘) der Art:
76. (+,1)
77. (-,1)
78. (0,+)
79. (0,-)
80. (a,+)
81. (a,-)
82. (1,+)
83. (1,-)
84. leidet an der gleichen Schwäche, wie schon zuvor bei der Diskussion seiner vier Quantorentypen, hier verstärkt um sein falsches Metaprinzip. Klammert man ‚affirmativ‘ als Einteilungskriterium aus, da dies auf alle Typen zutrifft, bleiben nur die beiden Quantoren und deren Verneinung:
85. Q=’alle‘,S,P
86. Q=(nicht)(alle),S,P $latex \leftrightarrow $ Q=(einige),S,(nicht),P
87. Q=’einige‘,S,P
88. Q=(nicht)(einige),S,P $latex \leftrightarrow $ Q=(alle),S,(nicht),P
89. Wollte man den umgangssprachlichen Quantor ‚keiner‘ benutzen, könnte man diesen über Typ 4b definieren: Q=’kein(er)‘,S,P $latex \leftrightarrow$ Q=(alle),S,($latex \neg$),P).

Fortsetzung folgt …

QUELLEN

  • Avicenna, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
  • Digital Averroes Research Environment
  • Stanford Encyclopedia of Philosophy, Aristotle’s Logic
  • Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7

Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER.

AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 8

Aussage, Aussagetypen, Avicenna, Disjunktion, Falsch, Knjunktion, Konjunktion, Logik, Logik - Alltag, Logik - Antike, Logik - formale, Negation, Operator, Operator - aussagenlogischer, Wahr, Wahrheit als Übereinstimmung, Wahrheitsbegriff, Wahrheitswert

VORGESCHICHTE

1. In einem ersten Beitrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 1 hatte ich geschildert, wie ich zur Lektüre des Textes von Avicenna gekommen bin und wie der Text grob einzuordnen ist. In einem zweiten Beitrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 2 ging es um die Frage, warum überhaupt Logik? Avicenna führt erste Unterscheidungen zu verschiedenen Wissensformen ein, lässt aber alle Detailfragen noch weitgehend im Dunkeln. Im Teil AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 3 ging es um einfache und zusammengesetzte Begriffe, und bei den einfachen Begriffen um ‚individuelle‘ und ‚universelle‘. Schon hier zeigt sich der fundamentale Unterschied zwischen der antiken und der modernen-formalen Logik. In der antiken Logik wird die Ausdrucksebene E – und einer sich daran manifestierenden Folgerungslogik – immer in Verbindung mit einer zugehörigen Bedeutungsstruktur gesehen, die sich an einer Objektstruktur O festmacht. Die moderne formale Logik kennt zwar auch ‚Semantiken‘ und ‚Ontologien‘, diese sind aber ’sekundär‘, d.h. es werden nur solche ‚formalen Semantiken‘ betrachtet, die zum vorausgesetzten syntaktischen Folgerungsbegriff ‚passen‘. Dies sollte dann später an konkreten Beispielen diskutiert werden. Hier liegt der Fokus auf der antiken Logik im Sinne Avicennas. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 4 knüpft Avicenna an den zuvor eingeführten Begriff des ‚universellen‘ Begriffs an und betrachtet jetzt solche als ‚universell‘ bezeichneten Ausdrücke in einem Ausdruckskontext von aufeinanderfolgenden Ausdrücken. Alle diese Ausdrücke könnte man im Sinne der antiken Logik auch als ‚Urteile‘ bezeichnen, durch die einem bestimmten Ausdruck durch andere Ausdrücke bestimmte Bedeutungen (Eigenschaften) zu- oder abgesprochen werden. Hier unterscheidet er die Fälle eines ‚wesentlichen‘ Zusammenhanges zwischen zwei Begriffen und eines ’nicht wesentlichen‘ – sprich ‚akzidentellen‘ – Zusammenhangs. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 5 führt Avicenna eine Reihe von neuen technischen Begriffen ein, die sich nicht alle in ihrer Bedeutung widerspruchsfrei auflösen lassen. Es handelt sich um die Begriffe ‚Genus‘, ‚Spezies‘, Differenz, allgemeine und spezielle Akzidens, den Begriff ‚Kategorie(n)‘ mit den Kategorien ‚Substanz‘, ‚Qualität‘ und ‚Quantität‘. Die Rekonstruktion führt dennoch zu spannenden Themen, z.B. zu einem möglichen Einstieg in das weltverändernde Phänomen der kognitiven Evolution. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 6 geht es um die Begriffe ‚Definition‘ und ‚Beschreibung‘. Im Verhältnis zwischen beiden Begriffen geht die Beschreibung der Definition voraus. In der ‚Definition‘, die Avicenna vorstellt, wird ein neuer Ausdruck e mittels anderer Ausdrücke <e1, …, ek>, die sich auf schon bekannte Sachverhalte beziehen, ‚erklärt‘. Die von Avicenna dann vorgenommene Erklärung, was eine ‚Definition‘ sei, hängt u.a. stark ab von dem Begriff der ‚Bekanntheit‘ und dem Begriff des ‚wahren Wesens‘. Für die Tatsache, dass ein Mensch A bestimmte Ausdrücke <e1, …, ek> einer Sprache L ‚kennt‘ oder ’nicht kennt‘, dafür gibt es keine allgemeinen Regeln oder Kriterien. Von daher macht die Verwendung der Ausdrücke ‚bekannt’/ ’nicht bekannt‘ eigentlich nur Sinn in solch einem lokalen Kontexten W* (z.B. einem Artikel, ein Buch, ein Vortrag, …), in dem entscheidbar ist, ob ein bestimmter Ausdruck e einer Sprache L schon mal vorkam oder nicht. Schwierig wird es mit dem Begriff des ‚wahren Wesens‘. In meiner Interpretation mit der dynamischen Objekthierarchie gibt es ‚das wahre Wesen‘ in Form von Objekten auf einer Stufe j, die Instanzen auf Stufen kleiner als j haben. Dazu gab es weitere Überlegungen. Im folgenden Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 7 beschreibt Avicenna syntaktisch zusammengesetzte, aber semantisch einfache Ausdrücke. Innerhalb der Ausdrücke unterscheidet er die Teileausdrücke ‚Name‘, ‚Verb‘ und ‚Präposition‘. Die unterschiedliche Charakterisierung erfolgt nicht aufgrund der syntaktischen Form, sondern aufgrund der semantischen Eigenschaften, die mit diesen Ausdrücken verbunden werden. Neben dem Objektbezug, der die eigentliche Bedeutung fundiert, gibt es im Bedeutungsraum auch noch den zeitlichen und den räumlichen Aspekt. Das Zusammenspiel von Bedeutung und Ausdruck wird angerissen.

AUSSAGEN/ FESTSTELLUNGEN – WAHR oder FALSCH

2. Nun wendet sich Avicenna zusammengesetzten (engl.: ‚compound‘) ‚Aussagen‘ (engl.: ‚proposition‘) bzw. ‚Feststellungen‘ (engl.: ’statements‘) bzw. ‚bekräftigende Rede‘ (engl.: ‚affirmative speech‘) zu.
3. Stillschweigend wird hier vorausgesetzt, dass eine Aussage mit den im vorausgehenden Abschnitt charakterisierten semantischen Ausdruckstypen (Name, Verb, Präposition) realisiert ist.
4. ‚Aussagen‘ [P] sind alle jene Ausdrücke E, von denen man sagen kann, sie treffen zu (sind ‚wahr‘), oder sie treffen nicht zu (sind ‚falsch‘); Aussagen sind eine echte Teilmenge aller Ausdrücke, $latex P \subset E$.
5. Avicenna unterscheidet drei Arten von Aussagen:
6. Beispiele für ‚kategorische‘ Aussagen sind (Der Mensch)(ist)(ein Lebewesen) bzw. (Der Mensch)(ist nicht)(ein Lebewesen).
7. Beispiele für ‚Disjunktiv-konditionelle‘ (engl.:‘ ‚disjunctive conditional‘) Aussagen sind (Etwas)(ist)(dies)(oder)(jenes) bzw. (Etwas)(ist nicht)(dies)(oder)(jenes) (oder: (Es ist nicht der Fall, dass)(Etwas)(ist)(dies)(oder)(jenes).
8. Beispiele für ‚Konjunktiv-konditionelle‘ (engl.:‘ ‚conjunctive conditional‘) Aussagen sind (Wenn)(dies)(der Fall ist)(dann)(ist auch)(das)(der Fall) oder (Weil)(dies)(der Fall ist)(ist)(auch)(das der Fall) oder (Und nicht)(Wenn)(dies)(der Fall ist)(oder)(das)(der Fall ist).

DISKUSSION

WAHR/FALSCH

9. Zunächst einmal die Formulierung, ‚dass etwas der Fall sei‘ als Kriterium für die Eigenschaft ‚wahr‘ und die Formulierung ‚dass etwas nicht der Fall sei‘ als Kriterium für die Eigenschaft ‚falsch‘.
10. Aussagen bilden eine Kombination aus Ausdruck e und Bedeutungskomponente m aus dem Bedeutungsraum M.
11. Vom Sprecher/ Hörer wird angenommen, dass er die Beziehung zwischen e und m ‚kennt‘, schreiben wir K(e,m) (für die Beziehung KNOW [K] mit $latex K \subseteq E \times M$).
12. Jetzt wird gesagt, dass eine solche Beziehung K(e,m) ‚zutreffen‘ kann oder ’nicht zutreffen‘ kann, bzw. ‚wahr’/ ‚falsch‘ sein kann.
13. Dies bedeutet, es muss einen zusätzlichen Aspekt, einen zusätzlichen Umstand Y geben, wodurch ein Sprecher/ Hörer zu solch einer Charakterisierung kommen kann.
14. Dieser zusätzliche Umstand Y muss ‚veränderlich‘ sein, d.h. er muss in einem Zustand Y_w auftreten, wodurch die Beziehung K(e,m) als ‚wahr‘ bezeichnet wird, und in einem Zustand Y_f, woraus ‚falsch‘ folgt. Möglicherweise gibt es auch noch eine neutrale Variante Y_n, bei deren Vorliegen man nicht weiß, ob es die Eigenschaft ‚wahr‘ oder ‚falsch‘ zutrifft.
15. Intuitiv wissen wir, dass wir zwar mit Ausdrücken e bestimmte Bedeutungen/ Vorstellungen m verknüpfen können, wir wissen aber auch, dass solche gewussten Sachverhalte m sich in der ‚realen Welt‘ W ändern können.
16. Zuvor haben wir schon die Annahmen entwickelt, dass sich eine dynamische Objekthierarchie O mittels $latex \kappa$ angeregt von Eigenschaften X der realen Welt W bilden lässt. D.h. die Objektstruktur O, die ein Teil des Bedeutungsraumes M ist – also auch Anteile in der Bedeutung m von der Beziehung K(e,m) haben kann –, ist nicht identisch mit den Eigenschaften X der realen Welt. Die Objektstruktur O ist ein ‚konstruiertes Bild über X‘. Von daher ist es denkbar, dass das konstruierte Bild O in M als Grundlage von K(e,m) zwar unveränderlich ist – es ist, wie es ist –, dass aber die auslösenden Eigenschaften X der realen Welt sich geändert haben, und sei es nur für einen Moment (t,t‘) mit t‘ > t.
17. Man könnte nun sagen, dass Beziehungen K(e,m) die sind, bei denen der Bedeutungsanteil m in dieser Beziehung so stark von einem X in der realen Welt abhängt, dass eine ‚Änderung von X‘ als ‚Differenz‘ wahrgenommen werden kann, d.h. es wird nicht direkt ein X oder ein verändertes X verglichen, sondern nur die ‚prozessierte Form‘ vom X über die Prozesse perc() und $latex \alpha$ unter Berücksichtigung von Raum und Zeit und Anzahl. So wie das gewusste ‚m‘ einem bestimmten Xm entspricht, so würde ein ‚Nicht-Xm‘, also $latex \overline{Xm}$ in der entsprechenden Form $latex nicht-m=\alpha(perc(\overline{X}))$ als ‚verschieden‘ von m erkannt/ aufgefasst/ verstanden.
18. Anders gesagt: Wenn wir in unserm Wissen von einer Beziehung K(e,m) ‚wissen‘, bei der wir ein Bedeutungselement ‚m‘ aus M ‚kennen‘, das durch unsere Interaktion mit der realen Welt W anlässlich bestimmter realer Welteigenschaften Xm ‚konstruiert‘ werden konnte also $latex m = \lambda(\alpha(perc(Xm)),M)$, – mit $latex O \subseteq M$ –, dann würde ein von Xm verschiedener Sachverhalt $latex \overline{Xm}$ auch eine unterschiedliche Bedeutungsrepräsentation $latex \overline{m} = \lambda(\alpha(perc(\overline{Xm})),M)$ hervorbringen können. Damit könnte unser ‚Wissen‘ im allgemeinen Bedeutungsraum M die beiden Bedeutungsobjekte ‚m‘ und ‚$latex \overline{m}$‘ direkt ‚vergleichen‘.
19. Wichtig wäre bei diesem Vergleich, dass hier die Zeitkomponente eine Rolle spielt. In der gewussten Beziehung K(e,m) ist die Zeit in gewisser Weise ‚aufgehoben‘, ’neutralisiert‘, für das Vergleichsobjekt ‚m‘ bzw. ‚$latex \overline{m}$‘ müsste gelten, dass es ‚aktuell‘ ist, ‚jetzt‘. Dann könnte man sagen, wenn eine Bedeutung ‚m‘ aus einer Wissensbeziehung K(e,m) über dem Bedeutungsraum M eine Entsprechung in einem ‚aktuellen m‘ finden kann (gebunden an eine aktuelle Wahrnehmung perc()), dann korrespondiert das gewusste ‚$latex m_{K}$‘ aus K(e,m) mit dem aktuell wahrnehmbaren ‚$latex m_{now}$‘. Ist dies nicht der Fall, lässt sich keine aktuelle Entsprechung zwischen einem gewusstem ‚$latex m_{K}$‘ aus K(e,m) zu einem wahrnehmbaren ‚$latex m_{now}$‘ finden, weil die aktuellen Bedeutungen ‚$latex \overline{m}_{now}$‘ anders sind.
20. In dieser Konstruktion gibt es in der Tat nur zwei Fälle: entweder findet sich zu einem gewussten m eine aktuelle Entsprechung ‚$latex m_{now}$‘ oder eben nicht. Dazwischen gibt es nichts. Ein ’neutrales‘ m kommt hier nicht zum Tragen. Denkbar wäre allerdings ein ‚Irrtum‘ in dem Sinne, dass das aktuell wahrgenommene ‚$latex \overline{m}_{now}$‘ zwar verschieden ist, dass diese Verschiedenheit aber entweder ‚falsch eingeschätzt‘ wird oder die Konstruktion des ‚$latex \overline{m}_{now}$‘ irgendwelche ‚Störungen‘, ‚Verzerrungen‘ aufweist, so dass das ‚$latex \overline{m}_{now}$‘ einige ‚Ähnlichkeiten‘ mit dem gewussten m aufweist, die zu einem Fehlurteil führen. Denn, nicht nur kann die aktuelle Konstruktion $latex \lambda$ Fehler aufweisen, sondern auch die auf ‚Erinnerung‘ basierende gewusste Beziehung K(e,m) kann Fehler aufweisen, die das gewusste m in die Nähe des aktuellen ‚$latex \overline{m}_{now}$‘ bringen. Also, Neutralität gibt es hier nicht, aber mögliche Irrtümer unterschiedlichster Art.

AUSSAGENTYPEN

21. Nach dieser Klärung, wie die Eigenschaft ‚wahr’/ ‚falsch‘ in dieser Rekonstruktion von Avicenna nachvollziehbar wären, geht es um die Frage, was es mit den drei Aussagetypen auf sich hat, die ich hier abkürzend ‚Kategorisierend‘, ‚Disjunktiv‘ und ‚Konjunktiv‘ bezeichne.
22. Im Fall des Aussagetyps ‚Kategorisierend‘ mit dem Beispiel (Der Mensch)(ist)(ein Lebewesen) bzw. (Der Mensch)(ist nicht)(ein Lebewesen) geht es offensichtlich nicht um einen Bezug zur aktuell realen Welt mit ihren realen Eigenschaften X, sondern um eine Beziehung zwischen zwei gewussten Bedeutungsstrukturen $latex m_{Mensch}$ und $latex m_{Lebewesen}$. Zwischen diesen beiden Bedeutungsstrukturen $latex m_{Mensch}, m_{Lebewesen}$ gibt es eine Beziehung der Art, dass die Bedeutungsstruktur $latex m_{Mensch}$ eine ‚Instanz‘ der Bedeutungsstruktur $latex m_{Lewesen}$ ist. Sofern dies der Fall ist wird durch eine Aussage der Art (Der Mensch)(ist)(ein Lebewesen) genau dieser Fall angesprochen. Wenn der Ausdruck (Der Mensch)(ist)(ein Lebewesen) mit den Verhältnissen der Bedeutungsstrukturen übereinstimmt (was man direkt wissen kann), dann trifft der gewusste Sachverhalt zu, andernfalls nicht. Natürlich kann es auch in diesem Fall prozessspezifische Fehler geben, die Bedeutungszuordnungen konstruieren, die falsch sind oder missverständlich oder verändert.
23. Im Fall der disjunktiven und konjunktiven Aussagetypen ist die Lage etwas unübersichtlicher, da Avicenna keine direkte Charakterisierung der beiden Aussagetypen mittels Wahrheitswerten vornimmt. Er erwähnt nur verschiedene Ausdrücke, denen man ‚intuitiv‘ eine Bedeutung zuordnen muss, und diese Beispiele sind – bei genauer Betrachtung – sogar widersprüchlich.
24. Bedient man sich des Hilfsmittels der Wahrheitswerttabelle, die zumindest in der stoischen Logik schon bekannt gewesen sein soll, dann kann man die beiden Aussagetypen Disjunktion und Konjunktion eindeutig charakterisieren. Dazu ist es hilfreich, die Ausdrücke von Avicenna ein wenig zu ’normieren‘.
25. DISJUNKTION: Statt zu schreiben (Etwas)(ist)(dies)(oder)(jenes), würde man umschreiben A=(Etwas)(ist)(dies) und B=(Etwas)(ist)(jenes), sodass der ganze Ausdruck lauten würde (A)(oder)(B), wobei sowohl A als auch B vom Typ ‚Aussage‘ sind, die ‚wahr‘ oder ‚falsch‘ sein kann. Dann könnte man sagen, dass ein Aussagetyp ‚Disjunktion‘ nur dann wahr ist, wenn wenigstens eine der beiden Teilaussagen A oder B wahr ist bzw. nur dann falsch ist, wenn beide Teilaussagen A und B falsch sind.
26. Den Fall, den Avicenna als ‚Konjunktives Konditional‘ einführt, ist nicht eindeutig. Es könnte entweder der späteren aussagenlogischen Konjunktion entsprechen oder auch der aussagenlogischen Implikation. Seine unvollständige Charakterisierung lässt beide Rekonstruktionen zu. Ich betrachte hier beide Fälle.
27. KONJUNKTION: Statt zu schreiben (Weil)(dies)(der Fall ist)(ist)(auch)(das der Fall) würde man im Fall der Konjunktion abkürzend schreiben A=(dies)(der Fall ist) und B=(das(ist)(der Fall). Dann könnte man sagen, der Ausdruck (A)(und)(B) ist nur wahr, wenn jeder der beiden Teilaussagen A und B wahr ist, und ist falsch, wenn wenigstens einer der beiden Teilaussagen falsch ist.
28. IMPLIKATION: Der Ausdruck (Wenn)(A)(dann)(B) ist nur falsch, wenn A wahr ist und B zugleich falsch; in allen anderen Fällen ist der Ausdruck wahr.
29. Disjunktion, Konjunktion und Implikation sind also Aussagetypen, die aus zwei Teilausdrücken A und B bestehen, die selbst wieder Aussagen sind, die wahr oder falsch sein können. Die beiden Teilausdrücke A und B werden dann durch die Teilausdrücke (oder), (und) sowie (wenn)-(dann)- verknüpft. Sie unterscheiden sich dadurch, wie der Wahrheitswert des Gesamtausdrucks von der Verteilung der Wahrheitswerte auf die Teilausdrücke festgelegt ist. Die Teilausdrücke (oder), (und) sowie (wenn)-(dann)- nennt man später dann auch ‚aussagenlogische Operatoren‘.
30. Man sieht hier leicht, dass der Aussagetyp ‚kategoriesierend‘ nicht in dieses Schema passt. Der Aussagetyp ‚kategorisierend‘ ist eine Aussage A, die wahr oder falsch sein kann unabhängig von irgendeinem aussagenlogischen Operator.

NEGATION

31. Die Verneinung von Aussagen hat man später dann auch anders geschrieben.
32. Statt zu schreiben (Etwas)(ist nicht)(dies)(oder)(jenes) hat man später geschrieben $latex \neg(A)(oder)(B)$ mit dem Zeichen $latex \neg$ für ’nicht‘ oder ‚es ist nicht der Fall, dass‘. Statt (oder) wurde später auch geschrieben $latex \vee$. Statt (und) das Zeichen $latex \wedge$. Dann bekommt man $latex \neg(A)(\vee)(B)$ bzw. $latex \neg(A)(\wedge)(B)$.

ERGEBNIS

33. Diese Rekonstruktionsansätze mögen genügen, um zu verdeutlichen, dass man eine plausible Semantik zur bisherigen Logik von Avicenna dazu konstruieren und dass man seine Aussagen zu Aussagetypen mit Wahrheitswerten letztlich mit den Konzepten der modernen Aussagenlogik versöhnen kann.
34. Was hier (noch) nicht gemacht wird, das ist die sich daraus ergebenden Konsequenzen in ihrer ganzen Breite zu entwickeln. Dies wird zu einem späteren Zeitpunkt geschehen.
35. Was die Semantik angeht, so kann man natürlich die Quintessenz der Semantik in einem formalen Modell auch noch viel einfacher fassen. Allerdings liegt das Interesse hier gerade darin, es nicht einfach nur zu vereinfachen, sondern es ganz speziell auch im Hinblick auf das Alltagsdenken und mit Blick auf die kognitiven Prozesse so zu verorten, dass die ‚Entstehung der Bedeutung‘ – zumindest prinzipiell – mit erfasst wird. Die Minimalforderung lautet, dass ein Ingenieur/ Informatiker in der Lage sein sollte, mit diesem Minimalmodell einen Roboter/ Softwareagenten zu bauen, der selbstständig die Bedeutung normalsprachlicher Ausdrücke von jeder Sprache für realweltliche Kontexte W erlernen kann.

Eine Fortsetzung findet sich HIER.

QUELLEN

  • Avicenna, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
  • Digital Averroes Research Environment
  • Stanford Encyclopedia of Philosophy, Aristotle’s Logic
  • Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7

Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER.

AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 7

Ausdruck, Ausdruck - einfacher, Ausdruck - sprachlicher, Ausdruck - zusammengesetzter, Avicenna, Bedeutung, Bedeutung eines Wortes, Bedeutungsbeziehung, Bedeutungsraum, Definition, Definition - explitite, Definition - rekursive, Definition - simultane, Logik, Logik - Alltag, Logik - Antike, Logik - formale, Modell, Objekt, Objekt - als Eigenschaft, Objekt - echtes, Objekthierarchie, Semantik, Struktur, Syntax

VORGESCHICHTE

1. In einem ersten Beitrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 1 hatte ich geschildert, wie ich zur Lektüre des Textes von Avicenna gekommen bin und wie der Text grob einzuordnen ist. In einem zweiten Beitrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 2 ging es um die Frage, warum überhaupt Logik? Avicenna führt erste Unterscheidungen zu verschiedenen Wissensformen ein, lässt aber alle Detailfragen noch weitgehend im Dunkeln. Im Teil AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 3 ging es um einfache und zusammengesetzte Begriffe, und bei den einfachen Begriffen um ‚individuelle‘ und ‚universelle‘. Schon hier zeigt sich der fundamentale Unterschied zwischen der antiken und der modernen-formalen Logik. In der antiken Logik wird die Ausdrucksebene E – und einer sich daran manifestierenden Folgerungslogik – immer in Verbindung mit einer zugehörigen Bedeutungsstruktur gesehen, die sich an einer Objektstruktur O festmacht. Die moderne formale Logik kennt zwar auch ‚Semantiken‘ und ‚Ontologien‘, diese sind aber ’sekundär‘, d.h. es werden nur solche ‚formalen Semantiken‘ betrachtet, die zum vorausgesetzten syntaktischen Folgerungsbegriff ‚passen‘. Dies sollte dann später an konkreten Beispielen diskutiert werden. Hier liegt der Fokus auf der antiken Logik im Sinne Avicennas. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 4 knüpft Avicenna an den zuvor eingeführten Begriff des ‚universellen‘ Begriffs an und betrachtet jetzt solche als ‚universell‘ bezeichneten Ausdrücke in einem Ausdruckskontext von aufeinanderfolgenden Ausdrücken. Alle diese Ausdrücke könnte man im Sinne der antiken Logik auch als ‚Urteile‘ bezeichnen, durch die einem bestimmten Ausdruck durch andere Ausdrücke bestimmte Bedeutungen (Eigenschaften) zu- oder abgesprochen werden. Hier unterscheidet er die Fälle eines ‚wesentlichen‘ Zusammenhanges zwischen zwei Begriffen und eines ’nicht wesentlichen‘ – sprich ‚akzidentellen‘ – Zusammenhangs. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 5 führt Avicenna eine Reihe von neuen technischen Begriffen ein, die sich nicht alle in ihrer Bedeutung widerspruchsfrei auflösen lassen. Es handelt sich um die Begriffe ‚Genus‘, ‚Spezies‘, Differenz, allgemeine und spezielle Akzidens, den Begriff ‚Kategorie(n)‘ mit den Kategorien ‚Substanz‘, ‚Qualität‘ und ‚Quantität‘. Die Rekonstruktion führt dennoch zu spannenden Themen, z.B. zu einem möglichen Einstieg in das weltverändernde Phänomen der kognitiven Evolution. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 6 geht es um die Begriffe ‚Definition‘ und ‚Beschreibung‘. Im Verhältnis zwischen beiden Begriffen geht die Beschreibung der Definition voraus. In der ‚Definition‘, die Avicenna vorstellt, wird ein neuer Ausdruck e mittels anderer Ausdrücke <e1, …, ek>, die sich auf schon bekannte Sachverhalte beziehen, ‚erklärt‘. Die von Avicenna dann vorgenommene Erklärung, was eine ‚Definition‘ sei, hängt u.a. stark ab von dem Begriff der ‚Bekanntheit‘ und dem Begriff des ‚wahren Wesens‘. Für die Tatsache, dass ein Mensch A bestimmte Ausdrücke <e1, …, ek> einer Sprache L ‚kennt‘ oder ’nicht kennt‘, dafür gibt es keine allgemeinen Regeln oder Kriterien. Von daher macht die Verwendung der Ausdrücke ‚bekannt’/ ’nicht bekannt‘ eigentlich nur Sinn in solch einem lokalen Kontexten W* (z.B. einem Artikel, ein Buch, ein Vortrag, …), in dem entscheidbar ist, ob ein bestimmter Ausdruck e einer Sprache L schon mal vorkam oder nicht. Schwierig wird es mit dem Begriff des ‚wahren Wesens‘. In meiner Interpretation mit der dynamischen Objekthierarchie gibt es ‚das wahre Wesen‘ in Form von Objekten auf einer Stufe j, die Instanzen auf Stufen kleiner als j haben. Dazu gab es weitere Überlegungen.

NAMEN, VERBEN/TERME, PRÄPOSITIONEN

2. Nach all den Vorüberlegungen nähert sich Avicenna nun dem eigentlichen Gegenstand der (antiken, auf das Alltagsdenken bezogenen) Logik, nämlich jenen ‚Ausdrücken‘, durch die entscheidende Bedeutungen kommuniziert werden.
3. Er beginnt mit ‚einfachen‘ Ausdrücken.

4. Er nimmt an, dass sich einfache Ausdrücke e aus drei Teilausdrücken zusammen setzen, die er als ‚Name‘, ‚Verb‘ und ‚Präposition‘ klassifiziert.

5. Terminologisch merkt er an, dass der grammatische Begriff ‚Verb‘ von Logikern ‚Term‘ genannt wird.

6. Sowohl der Name als auch das Verb sollen eine ‚vollständige Bedeutung‘ haben, Präpositionen dagegen nicht.

7. Namen unterscheiden sich von Termen dadurch, dass sie sich nicht auf eine ‚zeitliche Abfolge‘ (engl.: ‚temporal sequence‘) beziehen.

8. Verben hingegen – im Unterschied zu Namen – haben sowohl eine ‚Bedeutung‘ wie auch einen ‚zeitlichen Bezug‘ (engl.: ‚temporal significance‘).

9. Grenzfälle sind Namen wie ‚Heute‘ (engl.: ‚day‘) und ‚Gestern‘ (engl.: ‚yesterday). Obwohl sie einen ‚Teil der Zeit‘ (engl.: ‚part of time‘) bezeichnen (engl.: ’signify‘), sind sie doch keine Verben, da bei diesen Namen ihre ‚Bedeutung‘ mit dem ‚zeitlichen Bezug‘ zusammenfällt; bei einem Term wie ‚geschlagen‘ (engl.: ’struck‘) ist die Bedeutung (Vorgang des Schlagens) klar zu unterscheiden von dem Zeitbezug (der Vorgang war in der Vergangenheit).

10. Beispiele: e = <e1,e2,e3,e4,e5> = N:(Ich)Va:(habe)N:(den Zid)Vb:(gesehen); Der einfache Ausdruck e zerfällt in mehrere Ausdrucksteile <e1,e2,e3,e4,e5>, denen sich Bedeutungen zuordnen lassen. e1 = (Ich), bezieht sich auf den aktuellen Sprecher, und wird von daher als Name [N] für ein Objekt gewertet, das dem Namen eine Bedeutung verleiht. <e3, e4> = (den Zid) bezieht sich auf eine Person Zid, und wird auch als Name für ein Objekt gewertet, das dem Namen eine Bedeutung verleiht. e2 und e5 = (habe) … (gesehen) bezieht sich auf einen Vorgang des Sehens, bei der ein Beobachter etwas sieht (Bedeutungsanteil); zusätzlich wird ein zeitlicher Aspekt angedeutet, dass es sich um einen Vorgang in der Vergangenheit handelt. Ausdruck e1 füllt die ‚Rolle‘ des Beobachters und Ausdruck <e3, e4> spielt die Rolle des beobachteten Objekts.

11. Beispiel: e = <e1,e2,e3,e4> = N:(Zid) V:(ist) PRÄP:(im) N:(Haus). Der einfache Ausdruck e zerfällt in mehrere Ausdrucksteile <e1,e2,e3,e4>, denen sich Bedeutungen zuordnen lassen. e1 = N:(Zid) ist ein Ausdruck, der sich auf eine Person Zid bezieht, die dem Ausdruck als Objekt eine Bedeutung verleiht. e2 = V:(ist) ist ein Ausdruck, der sich auf einen Sachverhalt ‚etwas ist an einem Ort‘ bezieht, der dem Ausdruck sowohl eine Bedeutung verleiht wie auch eine davon unabhängige zeitliche Bestimmung, dass es in der Gegenwart ist. e3 = PRÄP:(im) ist ein Ausdruck, der sich auf einen räumlichen Sachverhalt bezieht ‚etwas ist in einem Raumgebiet‘, der dem Ausdruck eine Bedeutung verleiht, ohne expliziten Zeitbezug. e4 = N:(Haus) ist ein Ausdruck, der sich auf einen Ort Haus bezieht, der dem Ausdruck als Objekt eine Bedeutung verleiht. Die Kombination aus <e2, e3> ergibt einen Sachverhalt, der einerseits ein Objekt verlangt, von dem gesagt wird, dass es sich irgendwo befindet, und ein Objekt, das den Ort markiert. Beides ist mit e1 und e4 gegeben.

DISKUSSION

TERMINOLOGIE

12. Zur Terminologie: dass die (antiken) Logiker ‚Verben‘ als ‚Terme‘ bezeichnen sollen ist eine Sache. In diesem Kontext der Ausdrucksanalyse erscheint es mir eher verwirrend, zwei verschiedene Terminologien zu vermischen. Ich behalte im Folgenden die ‚grammatischen‘ Begriffe bei. Später kann man dann alle grammatischen Begriffe in einem mehr formalisierten logischen Kontext ‚übersetzen‘, falls notwendig.

13. Von ‚einfachen‘ Ausdrücken e zu sprechen, wenn die Ausdrücke sich alle aus mehreren Teilausdrücken e = <e1, e2, e3, …> zusammen setzen, kann verwirrend wirken, zumal er in vorausgehenden Abschnitten mit ‚einfachen‘ Ausdrücken tatsächlich solche meinte, die eben nicht zusammen gesetzt sind. Avicenna gibt keine direkte Erklärung für diese geänderte Verwendungsweise seines Begriffs eines ‚einfachen Ausdrucks‘, aber der Kontext legt folgende Interpretation nahe:

SYNTAX UND SEMANTIK

14. Es gibt eine ’syntaktische‘ Einfachheit (im Sinne von ’nicht zusammen gesetzt‘) und es gibt eine ’semantische‘ Einfachheit. Einfache Aussagen in diesem Abschnitt scheinen zu den ’semantisch einfachen‘ Ausdrücken zu gehören, denn syntaktisch sind sie eindeutig nicht einfach, sondern zusammengesetzt.

DER SEMANTISCHE RAUM

15. Damit stellt sich die Frage, wie man den ’semantischen Raum‘ ( den ‚Bedeutungsraum) eines Ausdrucks e (sowohl syntaktisch einfach als auch syntaktisch zusammengesetzt) so charakterisieren kann, dass man eine ‚einfache‘ Bedeutung von einer ’nicht einfachen = komplexen‘ Bedeutung unterscheiden kann.

16. Avicenna selbst hat ja in den vorausgehenden Abschnitten den ‚Bedeutungsraum‘ nicht ausdrücklich als eigenständigen Gegenstand thematisiert, immer nur indirekt, anhand von einzelnen Beispielen. Von diesen seinen indirekten, fragmentarischen Andeutungen aus lässt sich die Frage nach einer klaren Unterscheidung einer ‚einfachen‘ und einer ’nicht einfachen‘ Bedeutung im Kontext eines Ausdrucks e kaum einfach beantworten.

17. Als ‚Abfallprodukt‘ der bisherigen Rekonstruktion wurde das Konzept einer ‚dynamischen Objekthierarchie‘ O angedeutet, für die allgemeine Metaklassifikationen (entspricht in etwa dem klassischen Kategorienbegriff) wie z.B. ‚echtes Objekt‘ (etwa die Kategorie ‚Substanz‘), ‚unechte Objekte (etwa die Kategorie ‚Qualität‘), ‚Zeit‘, ‚Raum‘ und ‚Zahl‘ (etwa die Kategorie ‚Quantität‘) postuliert werden konnten.

18. Wenn man nun also von einem ‚Bedeutungsraum‘ (semantischen Raum) M sprechen will, dann müsste man entweder diese – bislang nur angedeuteten – Objektstrukturen mit den zusätzlichen Metaklassifikationen zugrunde legen oder eine Alternative formulieren. Ohne irgendwelche Annahmen dieser Art wäre der Begriff des semantischen Raumes vollständig leer und damit jegliche Art von Rekonstruktion von Ausdrücken e mit Bezug auf die zugehörigen ‚Bedeutungen‘ beliebig: alles wäre richtig und zugleich falsch.

19. Bis auf weiteres wird hier die bisherige Skizze zum dynamischen Objektraum mit den Metaklassifikationen als Arbeitshypothese für die weitere Interpretationen benutzt.

20. Von einem Ausdruck e mit Teilausdrücken <e1, e2, e3, …> zu sagen, dass bestimmte Ausdrucksteile $latex e_{i}$ bestimmte, voneinander abgrenzbare Bedeutungen haben, ihnen also unterschiedliche ’semantische Funktionen‘ zukommen, ist einerseits gewagt, da die Ausrücke als solche keinerlei syntaktische Hinweise haben müssen, aus denen man dies erkennen könnte, zugleich aber auch interessant, da damit die Denkaufgabe gestellt wird, wie es möglich sein soll, beliebige Ausdrucksteile $latex e_{i}$ in einem Ausdruck e durch Bezugnahme auf ‚etwas anderes‘, nämlich auf die ‚Bedeutung‘ indirekt charakterisieren zu können.

SIMULTANE DEFINITONEN

21. In gewissem Sinne könnte man hier auch von einem Definitionsvorgang sprechen: das Neue, das Unbekannte, das sind die Ausdruckselemente <e1, e2, e3, …> in einem Ausdruck e, das Bekannte das ist ein vorausgesetztes Bedeutungsgefüge, und die definitorische Erklärung ist die Verbindung von neuem Ausdruckselement und bekanntem Bedeutungsobjekt. Abweichend vom einfache Fall der expliziten syntaktischen Definition von einem Element e durch eine Folge von anderen Ausdrücken <e1, e2, e3, …> haben wir es hier im Falle der Definition von syntaktischen Ausdrücken durch Bezugnahme auf semantische Objekte mit zwei zusätzlichen Aspekten zu tun: (i) die Erklärung findet nicht in ein und demselben syntaktischen Raum statt sondern es werden zwei ansonsten getrennte Räume miteinander verknüpft: der syntaktische Raum mit dem semantischen Raum, und umgekehrt. Ferner (ii) wird nicht nur ein einziges syntaktisches Element ‚erklärt‘, sondern es werden mehrere syntaktische Elemente ‚parallel’/ ’simultan‘ erklärt.

22. Einen vergleichbaren Fall von ’simultaner‘ Erklärung haben wir im Falle von mathematischen Strukturtheorien, wie sie auch bei modernen empirischen Theorien auftreten. Ein typischer Fall wäre eine Struktur wie $latex < M, f1, …, fk >$. Hier werden mehrere Ausruckselemente eingeführt, deren Bedeutung sich erst im (syntaktischen) Gesamtkontext ergibt, der zusätzlich mit semantischen Elementen aufgeladen werden kann.

23. Ein anderes Beispiel sind formale Semantiktheorien, in denen zusammengesetzte Ausdrücke der Art e = <e1, e2, …> durch eine komplexe Abbildungsvorschrift so auf eine formale Struktur (auch ‚Domäne‘ oder ‚Modell‘ genannt) bezogen werden, dass für jeden syntaktisch zusammengesetzten Ausdruck e gesagt werden kann, wann das ‚Modell‘ M diese syntaktischen Ausdrücke ‚erfüllt‘, oft geschrieben $latex M \models e$ mit ‚e‘ als dem Ausdruck, der durch das Modell ‚erfüllt‘ wird.

24. Eine Besonderheit bei diesen Charakterisierungen von Ausdruckselementen e über den ‚Umweg‘ einer Bedeutungsstruktur M liegt darin, dass es nicht ausreicht, jedem einzelnen Teilausdruck $latex e_{i}$ eine – quasi isolierte – Bedeutung zuzuordnen, sondern die einzelnen bedeutungsfundierenden Objekte O der Bedeutungsstruktur M kommen in bedeutungsspezifischen Anordnungen (in Raum, Zeit, …) vor. Diese spezifischen Sachverhalte müssen in den Ausdruckselementen mitkodiert werden. Es reicht also nicht, nur zu sagen, dass das Ausdruckselement ‚e1‘ ein Objekt o1 bezeichnet, das für eine konkrete Person steht, sondern man muss zusätzlich auch – meistens – einen möglichen ‚Vorgang‘ benennen, in den das Objekt o1 eingebettet ist, und – meistens – zusätzlich mit einem zeitlichen Aspekt. Das wären dann schon mindestens drei verschiedene Kodierungsdimensionen, die im Bereich der Ausdruckselemente repräsentiert werden müssten.

25. Aufgrund der Beispiele von Avicenna gäbe es die zusätzlichen Arbeitshypothesen, dass (i) Vorgänge durch ‚Verben‘ [V] kodiert werden, (ii) zeitliche Aspekte sowohl durch Verben wie auch durch ‚Namen‘ [N], und (iii) räumliche Aspekte durch ‚Präpositionen‘ [PRÄP].

26. Die interessante Frage wäre natürlich, wie genau diese verschiedenen Objektstrukturen und -eigenschaften und -Relationen in der dynamischen Objekthierarchie O als dem Bedeutungsraum M repräsentiert sind. Sie müssten ja so vorliegen, dass man sie einfach ‚ablesen‘ könnte und dann durch einen entsprechenden ‚Übersetzungsprozeß‘ von M nach E zugeordnet werden könnten, also $latex \lambda: M \longrightarrow E$ (mit $latex \lambda $ als Übersetzungsvorschrift).

27. Nehmen wir das Beispiel e = <e1,e2,e3,e4> = N:(Zid) V:(ist) PRÄP:(im) N:(Haus). Es gibt hier (woher wissen wir dies überhaupt!) zwei Ausdruckselemente e1 und e4, die sich auf ‚echte Objekte‘ beziehen; e1 bezieht sich auf eine konkrete Personen, e4 auf ein Objekt, in dem Menschen sich aufhalten können. Der Ausdruck ist kein echtes Objekt, da es nur eine bestimmte Form von Beziehung zwischen zwei Objekten repräsentiert, nämlich dass ein Objekt A ‚räumlich in‘ einem anderen Objekt B vorkommt. Das Ausdruckselement e2 repräsentiert einen Zusammenhang zwischen zwei Objekten (echt oder unecht), der zudem aktuell ist, genauer: von einem Zielobjekt A wird gesagt, dass es in einer ist-Beziehung zu einem anderen Objekt steht. Da aber nach dem ‚Sprachgefühl‘ (was ist das?) die Kombination <e1, e2, e4> nicht geht, muss also <e3,e4> zusammen auftreten, damit e1 mittels e2 mit e4 kombiniert werden kann. Eine Arbeitshypothese könnte sein, dass echte Objekte, die mögliche ‚Orte des Vorkommens‘ bezeichnen, eine zusätzliche Präposition benötigen, um als Gegenpart in einer ist-Relation auf zu treten. Das ist natürlich hier alles sehr ad hoc und unsystematisch. Es kann aber verdeutlichen, dass die große Arbeitshypothese mit der bereichsübergreifenden Zuordnung $latex \lambda $ von Elementen einer Bedeutungsstruktur M (mit der dynamischen Objekthierarchie O als Teilstruktur) zu einer Menge E von möglichen Ausdrücken eine sehr detaillierte Beschreibung verlangt, die nicht ad hoc entscheidet, sondern systematisch.

Eine Fortsetzung zu diesem Beitrag findet sich HIER.

QUELLEN

  • Avicenna, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
  • Digital Averroes Research Environment
  • Stanford Encyclopedia of Philosophy, Aristotle’s Logic
  • Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7

Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER.

AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 6

Avicenna, Definiendum, Definiens, Definition, Logik, Logik - Alltag, Logik - Antike, Logik - formale

VORGESCHICHTE

1. In einem ersten Beitrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 1 hatte ich geschildert, wie ich zur Lektüre des Textes von Avicenna gekommen bin und wie der Text grob einzuordnen ist. In einem zweiten Beitrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 2 ging es um die Frage, warum überhaupt Logik? Avicenna führt erste Unterscheidungen zu verschiedenen Wissensformen ein, lässt aber alle Detailfragen noch weitgehend im Dunkeln. Im Teil AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 3 ging es um einfache und zusammengesetzte Begriffe, und bei den einfachen Begriffen um ‚individuelle‘ und ‚universelle‘. Schon hier zeigt sich der fundamentale Unterschied zwischen der antiken und der modernen-formalen Logik. In der antiken Logik wird die Ausdrucksebene E – und einer sich daran manifestierenden Folgerungslogik – immer in Verbindung mit einer zugehörigen Bedeutungsstruktur gesehen, die sich an einer Objektstruktur O festmacht. Die moderne formale Logik kennt zwar auch ‚Semantiken‘ und ‚Ontologien‘, diese sind aber ’sekundär‘, d.h. es werden nur solche ‚formalen Semantiken‘ betrachtet, die zum vorausgesetzten syntaktischen Folgerungsbegriff ‚passen‘. Dies sollte dann später an konkreten Beispielen diskutiert werden. Hier liegt der Fokus auf der antiken Logik im Sinne Avicennas. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 4 knüpft Avicenna an den zuvor eingeführten Begriff des ‚universellen‘ Begriffs an und betrachtet jetzt solche als ‚universell‘ bezeichneten Ausdrücke in einem Ausdruckskontext von aufeinanderfolgenden Ausdrücken. Alle diese Ausdrücke könnte man im Sinne der antiken Logik auch als ‚Urteile‘ bezeichnen, durch die einem bestimmten Ausdruck durch andere Ausdrücke bestimmte Bedeutungen (Eigenschaften) zu- oder abgesprochen werden. Hier unterscheidet er die Fälle eines ‚wesentlichen‘ Zusammenhanges zwischen zwei Begriffen und eines ’nicht wesentlichen‘ – sprich ‚akzidentellen‘ – Zusammenhangs. Im Abschnitt AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 5 führt Avicenna eine Reihe von neuen technischen Begriffen ein, die sich nicht alle in ihrer Bedeutung widerspruchsfrei auflösen lassen. Es handelt sich um die Begriffe ‚Genus‘, ‚Spezies‘, Differenz, allgemeine und spezielle Akzidens, den Begriff ‚Kategorie(n)‘ mit den Kategorien ‚Substanz‘, ‚Qualität‘ und ‚Quantität‘. Die Rekonstruktion führt dennoch zu spannenden Themen, z.B. zu einem möglichen Einstieg in das weltverändernde Phänomen der kognitiven Evolution.

DEFINITION UND BESCHREIBUNG

2. Der nächste Abschnitt handelt von ‚Definition‘ und ‚Beschreibung‘. Im Verhältnis zwischen beiden Begriffen geht die Beschreibung der Definition voraus.

3. In der ‚Beschreibung‘ mittels eines Ausdrucks e beziehe ich mich auf ‚etwas‘, ohne dass ich das ‚wahre Wesen‘ der Sache kennen muss, d.h. ich kann auch durch Bezug auf Teilaspekte beschreiben.

4. In der ‚Definition‘ mittels eines Ausdrucks e benutze ich andere Ausdrücke <e1, …, ek>, die sich auf schon bekannte Sachverhalte beziehen, und (idealerweise?) ist mir das wahre Wesen der zu beschreibenden Sache bekannt. In der Definition ‚beziehe‘ (engl.: ‚denote‘) ich mich auf etwas und zugleich grenze ich es ab von anderem.

5. Implizit kann man dem Text entnehmen, das der zu definierende Ausdruck e von dem definierenden Ausdruck <e1, …, ek> zu trennen ist; letzterer wird von Avicenna ‚definiens‘ genannt; dass der erste Ausdruck ‚definiendum‘ heißt, wird implizit unterstellt.

6. Avicenna weist auf vier hauptsächliche Fehler hin, die man beim Definieren begehen kann; ich fasse sie hier in zwei Fällen zusammen: (i) ‚Zirkularität‘: Wenn der zu definierende Ausdruck e selbst auch bei den definierenden Ausdrücken <e1, …, e, …, ek> vorkommt; (ii) ‚Unklarheit‘: Wenn mindestens einer der definierenden Ausdrücke <e1, …, ek> nicht bekannt genug ist. Im Fall (i) setze ich das, was ich definieren will, schon als bekannt voraus und im Fall (ii) ist das, wodurch ich etwas erklären möchte, selbst auch erklärungsbedürftig.

DISKUSSION

7. Die von Avicenna vorgenommene Erklärung, was eine ‚Definition‘ sei hängt u.a. stark ab von dem Begriff der ‚Bekanntheit‘ und dem Begriff des ‚wahren Wesens‘.

8. Zu sagen, dass die die Bedeutung eines neuen Ausdrucks e (der zu definierende Ausdruck, das Definiendum) zurückgeführt werden soll auf ’schon bekannte‘ Ausdrücke (die definierenden Ausdrücke, das Definiens) klingt im ersten Moment sehr plausibel, erweist sich bei näherer Betrachtung aber als ein schwieriges Kriterium.

9. Für die Tatsache, dass ein Mensch A bestimmte Ausdrücke <e1, …, ek> einer Sprache L ‚kennt‘ oder ’nicht kennt‘, dafür gibt es keine allgemeinen Regeln oder Kriterien; der eine mag zu einem bestimmten Zeitpunkt wissen, was mit DNA gemeint ist, die andere nicht.

10. Von daher macht die Verwendung der Ausdrücke ‚bekannt’/ ’nicht bekannt‘ eigentlich nur Sinn in solch einem lokalen Kontexten W* (z.B. einem Artikel, ein Buch, ein Vortrag, …), in dem entscheidbar ist, ob ein bestimmter Ausdruck e einer Sprache L schon mal vorkam oder nicht. Darüber hinaus kann man dann nur sagen, dass derjenige, der sich in den lokalen Kontext W* begibt, die ‚Voraussetzungen für W*‘ kennen sollte (in einer Schule/ Universität setzt z.B. der Lehrstoff von Stufe j normalerweise Wissen aus einer Stufe j-1 voraus).

11. Noch schwieriger wird es mit dem Begriff des ‚wahren Wesens‘. Das ‚Wesen‘ war uns schon begegnet im Kontext der Rede über ‚universelle Begriffe‘, deren Instanzen ‚wesentlich‘ bezogen sind auf den Oberbegriff. Dabei wurde hier als Interpretationsrahmen die dynamische Objekthierarchie O angenommen, die aus sinnlichen Wahrnehmungs- und Abstraktionsprozessen hervorgeht.

12. In dieser unterstellten dynamische Objekthierarchie O gibt es ‚das wahre Wesen‘ in Form von Objekten auf einer Stufe j, die Instanzen auf Stufen kleiner als j haben. Unter Voraussetzung einer solchen Hierarchie kann man z.B. sagen – was auch Avicenna tut –, dass (der Mensch)(ist)(ein Lebewesen). Zusätzlich kann man abgrenzend sagen, dass der Mensch ‚Lachen‘ kann und ‚Sprechen‘; Eigenschaften, die man lange Zeit nur dem Menschen zugeschrieben hatte und keinem anderen Lebewesen.

13. Grundsätzlich ist solch ein Erklärungsansatz nachvollziehbar, er hat aber die Schwäche, dass jeder Mensch möglicherweise unterschiedliche Informationen zu ‚Lebewesen‘ angesammelt hat, und wie die Geschichte der Biologie zeigt (man denke beispielsweise nur an die großen Naturforscher Linné (1707 – 1778), Alexander v. Humboldt (1769 – 1859), und Darwin (1809 – 1882)), hat sich das gemeinschaftliche Wissen über die Natur in den letzten150 Jahren dramatisch weiter entwickelt. Dies bedeutet, dass das grundsätzliche Modell Sinn macht, was aber zu einem bestimmten Zeitpunkt das ‚wahre Wesen‘ einer Sache ist, das ist jeweils neu zu überprüfen. Dazu kommt, dass im Jahr 2014 die Wissensmenge in jedem Gebiet dermaßen angewachsen ist, dass es immer schwieriger wird– selbst für Experten –, abschließend festzustellen, was denn jetzt alles tatsächlich bekannt ist.

14. Im übrigen sei angemerkt, dass es in der modernen Logik und Mathematik zusätzliche Definitionsformen gibt. Eine, die sehr wichtig ist, sei hier erwähnt, das ist die Definition, die einem rekursiven Schema folgt. Bei dieser Definition wird zwar auch das Neue durch das schon Bekannte erklärt, aber bei dem, was erklärt wird, handelt es sich nicht um ein statisches Objekt, sondern um einen Erzeugungsprozess, bei dem man mit einem bekannten Objekt o anfängt und dann auf dieses Projekt wiederholt eine bestimmte bekannte Operation f anwendet, die so geartet ist, dass man die Operation auch wieder auf das Ergebnis der Operation anwenden kann. Klassisches Beispiel ist die Erzeugung der natürlichen Zahlen. Die Operation heißt ‚Nachfolger‘ [Nf]. Angewendet auf ein Startobjekt o mit Nf(o) bekommt man ein Nachfolgeobjekt o‘, das genau definiert ist. Auf dieses kann man wieder die Nachfolgeoperation anwenden Nf(Nf(o)) = o“, usw. Auf diese Weise kann man über einen Erzeugungsprozess abzählbar unendlich viele neue Objekte allein dadurch definieren, dass man die Vorschrift für den Prozess hinschreibt: wenn o eine natürliche Zahl $latex \mathcal{N}$ ist, dann ist auch Nf(o) eine natürliche Zahl $latex \mathcal{N}$. Was definiert wird, das ist die abzählbar unendlich Menge aller natürlichen Zahlen. Was bekannt ist, das ist ein Anfangselement und eine einfache Operation.

Eine fortsetzung findet sich HIER.

QUELLEN

  • Avicenna, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
  • Digital Averroes Research Environment
  • Stanford Encyclopedia of Philosophy, Aristotle’s Logic
  • Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7

Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER.

AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 5

Akzidenz, Avicenna, Bedeutung, Bedeutung - abstraktes Konstrukt, Bedeutung - akzidentell, Bedeutung - kontingent, Bedeutung - wesentliche, Evolution, Evolution - biologische, Evolution - kognitive, Evolution - kulturelle, Genus, Kategorien, Logik, Logik - Alltag, Logik - Antike, Logik - formale, Mensch, Objekt, Objekt - als Eigenschaft, Objekt - echtes, Objekt - kontingent, Objekt - universell, Qualität, Quantität, Raum, Spezies, Substanz, Zeit

VORGESCHICHTE

1. In einem ersten Beitrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 1 hatte ich geschildert, wie ich zur Lektüre des Textes von Avicenna gekommen bin und wie der Text grob einzuordnen ist.
2. In einem zweiten Beitrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 2 ging es um die Frage, warum überhaupt Logik? Avicenna führt erste Unterscheidungen zu verschiedenen Wissensformen ein, lässt aber alle Detailfragen noch weitgehend im Dunkeln.
3. Im Teil AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 3 ging es um einfache und zusammengesetzte Begriffe, und bei den einfachen Begriffen um ‚individuelle‘ und ‚universelle‘. Schon hier zeigt sich der fundamentale Unterschied zwischen der antiken und der modernen-formalen Logik. In der antiken Logik wird die Ausdrucksebene E – und einer sich daran manifestierenden Folgerungslogik – immer in Verbindung mit einer zugehörigen Bedeutungsstruktur gesehen, die sich an einer Objektstruktur O festmacht. Die moderne formale Logik kennt zwar auch ‚Semantiken‘ und ‚Ontologien‘, diese sind aber ’sekundär‘, d.h. es werden nur solche ‚formalen Semantiken‘ betrachtet, die zum vorausgesetzten syntaktischen Folgerungsbegriff ‚passen‘. Dies sollte dann später an konkreten Beispielen diskutiert werden. Hier liegt der Fokus auf der antiken Logik im Sinne Avicennas.
4. Im nächsten Abschnitt VICENNAS ABHANDLUNG ZUR LOGIK – Teil 4 knüpft Avicenna an den zuvor eingeführten Begriff des ‚universellen‘ Begriffs an und betrachtet jetzt solche als ‚universell‘ bezeichneten Ausdrücke in einem Ausdruckskontext von aufeinanderfolgenden Ausdrücken . Alle diese Ausdrücke könnte man im Sinne der antiken Logik auch als ‚Urteile‘ bezeichnen, durch die einem bestimmten Ausdruck durch andere Ausdrücke bestimmte Bedeutungen (Eigenschaften) zu- oder abgesprochen werden. Hier unterscheidet er die Fälle eines ‚wesentlichen‘ Zusammenhanges zwischen zwei Begriffen und eines ’nicht wesentlichen‘ – sprich ‚akzidentellen‘ – Zusammenhangs.

BEGRIFFSINFLATION

5. Im nächsten Abschnitt führt er mindestens fünf neue technische Begriffe ein, deren Erklärung partiell unvollständig bleibt. Dies ist sehr schade. Aber, versuchen wir zu verstehen, was noch verstehbar ist.
6. Es sind die Begriffe ‚Genus‘ (Gattung?), ‚Spezies‘ (Art?), Differenz, allgemeine und spezielle Akzidens, und den Begriff ‚Kategorie(n)‘.
7. Er beginnt die Diskussion mit der ‚universellen Bedeutung‘, von der er behauptet, man könne hier 5 Typen unterscheiden (ohne sie direkt anzugeben). Drei Typen von universellen Bedeutungen seien ‚wesentlich‘ und zwei ’nicht-wesentlich‘, also ‚akzidentell‘.
8. Seine Erklärungen zu den ‚wesentlich universellen‘ Bedeutungen wiederholt in gewisser Weise das bislang Gesagte, indem er das Klassifizierungsmerkmal als Frage formuliert: ‚Zu welcher Art Y von Dingen gehört eine Entität X‘? Die Antwort wäre allgemein: ‚X ist ein Y‘, eventuell noch ergänzt um charakteristische Eigenschaften wie ‚Y ist/ hat/kann … Z‘. Letztlich ist dies, wie Avicenna feststellt, eine Definition, bei der etwas Neues (das X) durch Bezugnahme auf etwas schon Bekanntes (Y) erklärt wird. Y ist eine notwendige Voraussetzung für X.
9. Als Beispiel führt er u.a. an, Frage: ‚Was ist ein X=Mensch?‘, Antwort: ‚X=Mensch ist ein Y=Lebewesen‘ (‚animal‘).
10. Allerdings benutzt er auch Beispiele, die von dem ‚üblichen‘ Konzept eines Dings (einer ‚Entität‘ (engl.: ‚entity‘)) abweichen. Statt von ‚Mensch‘, ‚Kuh‘ und ‚Pferd‘ spricht er auch von ‚Schwarzheit‘, ‚Rotheit‘ und ‚Weisheit‘ bzw. auch von ‚Drei‘, ‚Fünf‘ und ‚Zehn‘.
11. Bedeutungen X = {‚Schwarzheit‘, ‚Rotheit‘, ‚Weisheit‘} beantwortet er mit Y=Qualitäten. Bedeutungen X = {‚Drei‘, ‚Fünf‘, ‚Zehn‘} beantwortet er mit Y=Zahlen.
12. Etwas später benutzt der die Bedeutungen ‚Substanz‘, ‚Qualität‘ und ‚Quantität‘ als universelle Begriffe für die ersten Beispiele, so dass man lesen kann/ muss Wenn X= {‚Mensch‘, ‚Kuh‘ und ‚Pferd‘}, dann Y= ‚Substanz‘, wenn X = {‚Schwarzheit‘, ‚Rotheit‘, ‚Weisheit‘} dann Y=Qualität, wenn X = {‚Drei‘, ‚Fünf‘, ‚Zehn‘} dann Y=Quantität.
13. Von den ‚wesentlichen universellen‘ Begriffen ‚Substanz‘, ‚Qualität‘ und ‚Quantität‘ sagt Avicenna, dass sie sich nicht weiter verallgemeinern lassen, d.h. wenn X=Substanz, dann gibt es kein allgemeineres Y, auf das sich dieser universelle Begriff zurückführen lässt (und entsprechend für X=Qualität‘ und X=Quantität). Deshalb nennt Avicenna diese universellen Begriffe, die wesentlich keinen anderen universellen Begriff mehr ‚über sich‘ haben, ‚Kategorien‘, ohne dass er diesen Zusammenhang explizit benennt; er tut es einfach.
14. Als Beispiele für ‚akzidentelle universelle‘ Begriffe führt er an, dass ‚fest‘ (engl.: ’solid‘) allgemeiner sei als ‚Lebewesen‘, aber spezieller als ‚Substanz‘; entsprechend sei ‚Zahl‘ allgemeiner als ‚gleich‘ (engl.: ‚even‘), aber spezieller als ‚Quantität‘. ‚Gleichheit (engl.: ‚eveness‘) sei allgemeiner als ‚vier‘, doch spezieller als ‚Quantität‘.
15. Dann führt er die Begriffe ‚Genus‘ und ‚Spezies‘ ein mit der Formulierung, dass dasjenige, das allgemeiner ist, die speziellere Spezies sei, und umgekehrt, dass dasjenige, was das speziellere Universelle ist, ist die allgemeinere Spezies. Diese Formulierungen sind nicht eindeutig.
16. Später sagt er noch, dass es Dinge gibt, die sowohl Genus und Spezies sein können oder Dinge, die nur Genus sind, und nicht unter irgendeiner Spezies sind.
17. Dann folgt die Feststellung, dass die Begriffe ‚Substanz‘, ‚Qualität‘ und ‚Quantität‘ kein Genus einer Spezies seien; unter ihnen befinden sich nur Instanzen wie ‚Mensch‘, ‚Schwarzheit‘ und ‚vier‘.
18. Aus diesen Beispielen folge die Natur einer Spezies, die kein Genus sein kann, sondern nur Spezies von allen Spezies, die ‚unter‘ ihr kommen.
19. Instanzen eines wesentlichen universellen Begriffs können sich durch akzidentelle Eigenschaften unterscheiden (z.B. angenommen {X1, X2} sind beide Y und X1 ist ’schwarz‘ und X2 ‚weiß‘ und ’schwarz‘. Dann ist die Eigenschaft ’schwarz‘ allgemeiner als X1 und X2, ’schwarz‘ kommt X1 und X2 nicht wesentlich, sondern akzidentell zu, kann aber differenzierend wirken.
20. Abschließend führt Avicenna noch folgende Beispiele an: Jeder universelle Begriff ist entweder Genus, so wie ‚Lebewesen‘, oder Spezies, so wie ‚Mensch‘, oder Differenz, so wie ‚die Fähigkeit zu Sprechen‘, oder ‚allgemein akzidentell‘ so wie ‚Bewegung‘, ‚Schwarzheit‘, ‚Weisheit‘.

INTERPRETATION- ANMERKUNGEN

21. War die Re-Lektüre und einsetzende Interpretation von Avicennas Text bis zu dieser Stelle relativ einfach, so zeigen sich jetzt erste Problemstellungen, die man nicht mehr so einfach ‚verworten‘ kann.
22. Einmal gibt es das Phänomen, dass er Begriffe einführt und benutzt, die nicht – zumindest auf einen ersten Blick – direkt erklärbar sind. Dann werden Zusammenhänge thematisiert, wo man sich die Frage stellen kann, ob er dies wirklich ‚gemeint‘ haben kann oder, falls ja, wie man damit umgehen will.
23. Dies gibt Gelegenheit, kurz ein paar Worte zum ‚Interpretieren‘ zu sagen. Ich werde dabei nicht auf die sehr umfangreiche Literatur zu diesem Thema eingehen (im Bereich Philosophie, Literatur und wissenschaftliche Bibelauslegung gibt es dazu nicht hunderte, sondern sicher tausende von Artikeln und Büchern. Einiges davon musste ich zu früheren Zeiten durcharbeiten). Ich beschränke mich hier auf jene Grundprinzipien, die ich hier anwenden möchte.
24. Die philologischen Fragen, ob die englische Übersetzung hier den arabischen Text korrekt wiedergibt, oder ob gar der arabische Text Überlieferungsfehler aufweist, kann ich hier nicht behandeln. Ich muss den Text nehmen, wie ich ihn vorfinde, und wenn sich für mich Unklarheiten ergeben, kann ich sie nur benennen und versuchen sie zu interpretieren.
25. Was die ‚Interpretation‘ (Auslegung, Deutung, …) des Textes angeht, so gibt es ja mindestens zwei verschiedene Ansprüche: (i) man will die ‚Bedeutung‘ rekonstruieren, die der Autor selbst mit dem verknüpft hatte (also eine Art ‚konservierende‘ Interpretation), oder (ii) man will die Bedeutung des Autors (des Textes) in einem anderen/ neuen Bedeutungsrahmen ‚rekonstruieren‘, ihn quasi von Bedeutungsraum R_Autor in den Bedeutungsraum R_Leser ‚übersetzen‘.
26. Beide Vorgehensweisen haben ihr Recht. Die ‚konservierende‘ Rekonstruktion ist idealerweise eigentlich der erste Schritt und die Voraussetzung für die ‚Neuinterpretation‘. Es ist aber eine offene Frage, ob ein Leser immer und überall über genau die Voraussetzungen in seinem Denken verfügt, dass er den ursprünglichen Bedeutungsraum R_Autor überhaupt eins-zu-eins rekonstruieren kann. Nach ca. 1000 Jahren, die uns von Avicenna trennen, ist es sogar ziemlich unwahrscheinlich, dass wir dies überhaupt noch können.
27. Hier, in dieser Rekonstruktion, werde ich erst gar nicht versuchen, den ursprünglichen Bedeutungsraum R_Autor zu rekonstruieren, da ich niemals wüsste, ob ich mit meinen Überlegungen ‚richtig‘ liege oder nicht. Dies Referenzproblem haben alle wissenschaftlichen Rekonstruktionen alter Texte (dies gilt natürlich auch für das hebräische Alte Testament, das griechische Neue Testament und den arabischen Koran).
28. Im weiteren Verlauf werde ich also die bisherigen Rekonstruktionsannahmen weiter verfolgen. Letztlich ist es eine Art ‚Test‘, ob und wie sich der Text von Avicenna in einem modernen erkenntnistheoretischen Modell ’neu lesen‘ lässt.

DISKUSSION

29. Bisher haben wir folgende allgemeine Annahmen bei der Rekonstruktion des Textes von Avicenna getroffen:
30. Die Ausdruckselemente E einer Sprache L sind nur ‚Zeiger‘, die auf irgendwelche kognitiven Objekte O hindeuten, die im Rahmen der generierten Zeigebeziehung M für die Ausdruckselemente E zu dem werden, was wir ihre Bedeutung nennen.
31. Die kognitiven Objekte O entstehen in einem Erzeugungsprozess, der Eigenschaften X der umgebenden Welt W über sinnliche Wahrnehmungsprozesse perc() und interne Abstraktionsprozesse $latex \alpha$ als irgendwelche Objekte O klassifiziert. Man könnte von daher auch sagen $latex \kappa = perc \otimes \alpha$, oder $latex \kappa(X, O) = O$.
32. Wir hatten ferner noch unterschieden zwischen ‚echten‘ Objekten, d.h. solchen Bündelungen von Objekten, die als solche in der umgebenden Welt W ‚vorkommen‘ und und solchen ‚unechten‘ Objekten, die zwar gebildet werden können, die aber immer nur ‚als Teil anderer Objekte‘ auftreten können. Die Definition von ‚wesentlich universellen Objekten‘ von Avicenna deckt sich mit dem Konzept ‚echter Objekte‘ und Avcennas Definition von ‚akzidentellen universellen‘ Objekten deckt sich mit den unechten Objekten, die anderen Objekten zukommen können, aber nicht müssen.

DISKUSSION – KATEGORIEN

33. Avicenna führt dann indirekt das Konzept von ‚(wesentlichen universellen) Kategorien‘ ein, die ich indirekt rekonstruiert habe als solche ‚wesentlich universellen Objekte‘, ‚über die‘ es keine weiteren Verallgemeinerungen mehr gibt. Da er es nur bei einzelnen Beispielen belässt ohne wirkliche Argumentationen bleibt hier einiges offen.
34. Die genannten drei Kategorien erscheinen wie eine Art ‚Meta-Klassifikation‘ über allen möglichen Objekten, so eine Art ‚Typisierung‘ der verschiedenen möglichen Objektbildungen. Versucht man im Bereich der Objektklassifikationen kriterien zu finden, welches Objekt zu welcher Kategorie gehört, wird es aber schnell schwierig.
35. Kategorie ‚Substanz‘: Wann ist ein Objekt eine ‚Substanz‘ und wann ‚Qualität‘ oder ‚Quantität‘? Ein erster Ansatzpunkt wäre zu sagen, dass alle ‚echten‘ Objekte ‚Substanzen‘ sind und alle ‚unechten‘ Objekte ‚Qualitäten‘. Was aber wäre dann mit den ‚Quantitäten‘? Die ‚Anzahl‘ von Objekten (echten wie unechten) ist ja keine ‚Eigenschaft an sich‘, sondern ist eher eine ‚Metaeigenschaft‘, die man vorhandenen (real oder gedachten) Objekten zuordnen kann. Im Vergleich zu Farben, Formen, Tönen usw., die auf Sinneseigenschaften aufsetzen, ist ‚Quantität‘ als Metaeigenschaft eine abgeleitete, sekundäre, abstrakte Eigenschaft, so wie z.B. auch ‚größer/ kleiner‘, ‚vorher/ nachher‘, ‚vorne/ hinten, ‚oben/ unten‘, usw. In allen genannten Fällen gibt es schon irgendwelche Objekte, zwischen denen räumliche, zeitliche – oder sonstige – allgemeine Beziehungen erkennbar sind. Diese indirekten, sekundären, abgeleiteten Beziehungen bilden dann eine eigene Klasse von ‚abstrakten‘ Eigenschaften, von denen die ‚Quantitäten‘ nur eine Teilmenge wären. Wenn also Avicenna schon die Kategorie ‚Quantität‘ bemüht, warum nicht auch ‚Raum‘ und ‚Zeit‘?
36. Alle diese Überlegungen zu ‚Kategorien‘ als zusätzliche Meta-Klassifikationen der generierbaren Objekte setzen allerdings voraus, dass es möglich ist, im Bereich der Objekthierarchie für alle Objekte O solche ‚Kontexte‘ annehmen zu können, durch die sie bzgl. ‚Substanz‘, ‚Qualität‘, ‚Quantität‘, ‚Raum‘ und ‚Zeit‘ charakterisierbar werden. Im bisher verfolgten Modell würde dies bedeuten, dass Objekte nicht nur über ihre ‚direkten‘ sensorischen Eigenschaften $latex K_{s}$ generiert werden, sondern sie werden von vornherein auch mit minimalen ‚Raumanteilen‘ bzw. in bestimmten ‚Abfolgen‘ ‚gespeichert‘ bzw. sind sensitiv bzgl. Abfolgen ‚erinnerbar‘.

DENKEN ALS KOGNITIVE EVOLUTION

37. Oder, wenn schon, dann noch allgemeiner: der gesamte Objekterzeugungsprozess $latex \kappa$ mus so beschaffen sein, dass er die fundamentalen Eigenschaften X der umgebenden Welt so in die Objekthierarchie übersetzt, dass (i) echte und unechte Objekteigenschaften hinreichend erhalten bleiben können, dass (ii) räumliche und zeitliche Verhältnisse hinreichend repräsentiert werden können, dass (iii) quantitative Verhältnisse erzeugt werden können (z.B. Aufzählungen und Äquivalenzklassen), dass (iv) neben den Eigenschaften, die ‚gegeben‘ sind (IST, real), auch ’neue‘ Kombinationen erzeugt werden können (Möglichkeit, Potenz, kombinatorischer Raum), und dass (v) neue Kombinationen (Möglichkeiten) mit dem ‚realen Raum‘ verglichen werden können.
38. Sofern dies möglich ist (und alles, was wir über das menschliche Denken heute wissen, bestätigt dies), kann man dann diese Art von Denken als Fortsetzung der biologischen Evolution im Bereich des Denkens (quasi als kognitive Evolution) betrachten, d.h. die biologische Evolution hat – mit ihrem kombinatorischen genetischen Mechanismus – Strukturen geschaffen (Körper mit Gehirn), die in der Lage sind, die an die materiellen Strukturen gebundene Kombinatorik neuer Lebensformen über die Neuronennetze zu dynamisieren, zu beschleunigen, zu flexibilisieren. Mit der Kombinatorik des neuronalen Denkens konnte die biologische Evolution der Entwicklung neuer, leistungsfähigerer Lebensformen einen gewaltigen Schub im einzelnen Organismus verleihen; durch die Möglichkeit symbolischer Kombination können sich die neurologisch erzeugbaren neuen Denkräume zusätzlich direkt miteinander verschränken und die Entwicklung neuer Lebensformen in bis dahin ungeahnte Dimensionen katapultieren.
39. Doch zurück zur vorliegenden Interpretationsaufgabe.

GENUS – SPEZIES

40. Bislang haben wir ansatzweise eine Rekonstruktion des Konzeptes von ‚Kategorien‘ als Meta-Klassifikationen im Bereich der dynamischen Objekthierarchie.
41. Unklar, da widersprüchlich, bleibt bei Avicenna die Verwendung der Begriffe ‚Genus‘ und Spezies‘. Eine erste, einfache, und nachvollziehbare Interpretation wäre die, jedes Objekt als ein ‚Genus‘ zu bezeichnen, das ‚Instanzen‘ besitzt, denen ‚differenzierende‘ Eigenschaften zukommen (wie auch die verschiedenen Genus-Objekte sich voneinander durch Eigenschaften unterscheiden). ‚Spezies‘ wären dann jene voneinander abgrenzbaren Instanzen (vgl. auch Carl von Linné (1707 – 1778), sein Werk ‚Systema Naturae‘), die einem Genus ‚untergeordnet‘ wären. Allerdings kommen die Begriffe ‚Genus‘ und ‚Spezies‘ im Text mehrfach in Verwendungen vor (z.B. auch als ‚Spezies der Spezies‘), die sich – aus meiner Sicht – einer schlüssigen Interpretation entziehen.

ALLGEMEINE UND SPEZIELLE AKZIDENZ

42. Mit den Begriffen ‚allgemeine‘ und ’speziellen‘ Akzidenzien verhält es sich ähnlich: es gäbe eine einfache, nachvollziehbare Interpretation, aber diese deckt nicht alle Verwendungsweisen dieser Begriffe ab.
43. Ausgangspunkt sind ja nicht-zusammengesetzte Ausdrücke mit einer universellen Bedeutung, bei der zwischen ‚wesentlichen‘ und ‚akzidentellen‘ unterschieden wurde. Die ‚akzidentellen universellen Begriffe wurden zuvor schon als ‚unechte Objekte‘ rekonstruiert, die niemals isoliert auftreten können, sondern immer nur als Teile von echten (wesentlichen universellen) Objekten. Insofern sind sie ‚akzidentell‘ und eine informelle abkürzende Redeweise könnte sie als ‚Akzidentien‘ bezeichnen, verstanden als Eigenschaften, die bei einem Objekt auftreten können, aber nicht müssen.
44. Wäre zu klären, was ‚allgemeine‘ von ’speziellen‘ Akzidenzien unterscheidet. Hier nochmals die Beispiele aus dem Text, wonach ‚fest‘ (engl.: ’solid‘) allgemeiner sei als ‚Lebewesen‘, aber spezieller als ‚Substanz‘; entsprechend dass ‚Zahl‘ allgemeiner sei als ‚gleich‘ (engl.: ‚even‘), aber spezieller als ‚Quantität‘, und schließlich dass ‚Gleichheit (engl.: ‚eveness‘) allgemeiner sei als ‚vier‘, doch spezieller als ‚Quantität‘.
45. Die Eigenschaft ‚fest‘ ist nach bisheriger Rekonstruktion klar ein unechtes Objekt, d.h. eine akzidentelle Eigenschaft, die als Teil von echten Objekten auftreten kann. Zu sagen, dass diese akzidentelle Eigenschaft allgemeiner sei als ‚Lebewesen‘, aber spezieller als ‚Substanz‘, macht nicht unbedingt Sinn, genauso wenig wie es Sinn machen würde, Hühner mit Grashalmen zu vergleichen. Es sei denn, es gäbe einen ‚übergreifenden Aspekt‘, auf den sich beide, die Hühner und die Grashalme, beziehen lassen würden.
46. Ich kann in diesem Zusammenhang keinen solchen übergreifenden Gesichtspunkt erkennen. Bestimmte akzidentelle Eigenschaften können bei Objekten auf verschiedenen Stufen der Objekthierarchie auftreten. Hier ein Beziehungsgeflecht zwischen den Eigenschaften konstruieren zu wollen überzeugt mich nicht.

ALLGEMEINE EINSCHÄTZUNG

47. Schon an dieser Stelle der Relektüre von Avicennas Logik deutet es sich an, dass Avicenna viele seiner technischen Begriffe nur unzulänglich erklärt und voneinander abgrenzt. Ein Grund dafür kann sein, dass er die das Konzept der Objekterstehung und der Objekthierarchie als Gegenpol zu den Ausdrücken offenbar nicht als eigenständiges System systematisch entwickelt. In anderen Interpretationsprojekten (z.B. bei Nicolai Hartmann) musste ich die Rekonstruktion irgendwann einfach abbrechen, da der Text in sich irgendwann so widersprüchlich war, dass ein sinnvolles Weiterlesen nicht mehr möglich erschien.

Fortsetzung folgt …

QUELLEN

  • Avicenna, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
  • Digital Averroes Research Environment
  • Stanford Encyclopedia of Philosophy, Aristotle’s Logic
  • Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7

Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER.

AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 4

Avicenna, Bedeutung, Bedeutung - abstraktes Konstrukt, Bedeutung - akzidentell, Bedeutung - kontingent, Bedeutung - wesentliche, Bedeutung eines Wortes, Bedeutungsbeziehung, Bedeutungsmaterial, Logik, Logik - Alltag, Logik - Antike, Logik - formale, Metaphysik, Objekt, Objekt - als Eigenschaft, Objekt - echtes, Objekt - kontingent, Objekt - universell, Objekttyp, Ontologie

VORGESCHICHTE

1. In einem ersten Beitrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 1 hatte ich geschildert, wie ich zur Lektüre des Textes von Avicenna gekommen bin und wie der Text grob einzuordnen ist.
2. In einem zweiten Beitrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 2 ging es um die Frage, warum überhaupt Logik? Avicenna führt erste Unterscheidungen zu verschiedenen Wissensformen ein, lässt aber alle Detailfragen noch weitgehend im Dunkeln.
3. Im Teil AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 3 ging es um einfache und zusammengesetzte Begriffe, und bei den einfachen Begriffen um ‚individuelle‘ und ‚universelle‘. Schon hier zeigt sich der fundamentale Unterschied zwischen der antiken und der modernen-formalen Logik. In der antiken Logik wird die Ausdrucksebene E – und einer sich daran manifestierenden Folgerungslogik – immer in Verbindung mit einer zugehörigen Bedeutungsstruktur gesehen, die sich an einer Objektstruktur O festmacht. Die moderne formale Logik kennt zwar auch ‚Semantiken‘ und ‚Ontologien‘, diese sind aber ’sekundär‘, d.h. es werden nur solche ‚formalen Semantiken‘ betrachtet, die zum vorausgesetzten syntaktischen Folgerungsbegriff ‚passen‘. Dies sollte dann später an konkreten Beispielen diskutiert werden. Hier liegt der Fokus auf der antiken Logik im Sinne Avicennas.

WESENTLICHE UND NICHT-WESENTLICH (AKZIDENTIELL, KONTINGENT…)

4. Im nächsten Abschnitt knüpft Avicenna an den zuvor eingeführten Begriff des ‚universellen‘ Begriffs an, das sind jene, die zwar eine Bedeutung haben, diese Bedeutung kann aber verschiedene konkreten ‚Instanzen‘, ‚Realisierungen‘, ‚Beispiele‘ umfassen (also: der Ausdruck ‚Tasse‘ kann sich auf viele verschiedene konkrete Tassenobjekte beziehen).
5. Er betrachtet jetzt solche als ‚universell‘ bezeichneten Ausdrücke in einem Ausdruckskontext von aufeinanderfolgenden Ausdrücken mit den folgende Kombinationen von Ausdrücken (hier in deutscher Übersetzung): (i) ‚Der Mensch ist ein Lebewesen‘, (ii) ‚Vier ist eine Zahl‘, (iii) ‚Der Mensch existiert‘, (iv) ‚Zahlen existieren‘, (v) ‚Der Mensch ist weiß‘, (vi) ‚Der Mensch ist nicht weiß‘, (vii) ‚Der Mensch lacht‘, (viii) ‚Zid sitzt‘, (ix) ‚Zid schläft‘, (x) ‚Zid ist alt‘, (xi) ‚Zid ist jung‘.
6. Alle diese Ausdrücke könnte man im Sinne der antiken Logik auch als ‚Urteile‘ bezeichnen, durch die einem bestimmten Ausdruck durch andere Ausdrücke bestimmte Bedeutungen (Eigenschaften) zu- oder abgesprochen werden (z.B. wird in (v) dem Objekt (der Mensch) die Eigenschaft (weiß) zugesprochen).
7. Er nimmt folgende interessante Unterscheidung vor: (i) er betrachtet sowohl ‚universelle‘ Ausdrücke wie ‚Mensch‘, ‚Zahl‘, ‚Lebewesen‘, Vier‘ und einen ‚individuellen‘ Ausdruck wie ‚Zid‘ als Bezeichnung eines konkreten Objektes, das als Instanz eines ‚Menschen‘ genommen wird, und (ii) sagt dann, dass die Bedeutung (‚meaning‘) dieser Ausdrücke sich aus dem ‚Wesen‘ des Objektes ergibt. D.h. dasjenige, was wir aufgrund unserer sinnlichen Wahrnehmung in Verbindung mit unseren Denkprinzipien als Objekt ‚Mensch‘ oder ‚Vier‘ oder ‚Zahl‘ oder ‚Zid‘ abstrahierend erkennen können, das ergibt sich nicht einfach so, nicht zufällig, nicht kontingent, nicht akzidentiell, sondern dies ergibt sich aus dem ‚Wesen‘ des Objektes, und zwar notwendig, zwingend, eben ‚essentiell‘, ‚wesenhaft‘.
8. In der Ausdrucksfolge (Der Mensch) (ist) (weiß) wird eine Beziehung zwischen der Bedeutung des Ausdrucks (der Mensch) und (weiß) durch Verwendung des Ausdrucks (ist) hergestellt. In der ’normalen Verwendung‘ bedeutet dies, dass die Bedeutung von (weiß) der Bedeutung von (der Mensch) zugesprochen wird.
9. Doch aus der Kenntnis der Bedeutung des Ausdrucks (der Mensch) folgt nach Avicenna nicht notwendigerweise die Kenntnis der Bedeutung des Ausdrucks (weiß) als Teil von (der Mensch). Die Begründung von Avicenna: zum ‚Wesen‘ des Menschen gehört es nicht, dass er ‚weiß‘ ist; er kann ‚weiß‘ sein, aber er muss nicht.
10. Das ist die entscheidende Argumentationsfigur: charakteristisch für ‚wesentliche‘ Ausdrücke ist es, dass deren Bedeutung sich auf Objekte bezieht, denen aufgrund ihres ‚Wesens‘ bestimmte Eigenschaften notwendig zukommen, andere aber nicht.
11. Doch lassen die Sätze von Avicenna noch eine weitere Deutung zu. Im Fall von ‚universellen‘ Ausdrücken unterscheidet er ja die universelle (eine) Bedeutung von den möglichen ‚Instanzen‘ (in der englischen Übersetzung wird ‚Instanz‘ als ein ‚particular‘ bezeichnet). Die Frage ist, ob und inwieweit sich die Eigenschaften der universellen Bedeutung auf die Instanzen überträgt.
12. Hier benutzt Avicenna zwei Gedanken: (i) Er sagt, dass die ‚Existenz‘ der universellen Bedeutung die Voraussetzung (‚prerequisite‘) für die ‚Existenz‘ der besonderen Bedeutung ist und (ii) dass die besondere Bedeutung aus der universellen Bedeutung folgt.
13. Also, wenn der Ausdruck (der Mensch) (ist) (ein Lebewesen) Sinn machen soll, dann muss die allgemeine Bedeutung von ‚Lebewesen‘ gegeben sein und es muss klar sein, dass ‚Mensch‘ eine Instanz (in der englischen Übersetzung ein ‚particular‘) von der allgemeinen (wesentlichen) Bedeutung ‚Lebewesen‘ ist; entsprechend setzt der Name ‚Zid‘ die Existenz der allgemeinen Bedeutung von ‚Mensch‘ voraus.
14. Interessant ist noch das Detail, dass Avicenna die ‚Seele‘ als wesentlich zur Bedeutung von ‚Mensch‘ gehörig ansieht. Bedenkt man, wie schwierig (bis unmöglich?) es ist, die Bedeutung von ‚Seele‘ zu klären, kann es zumindest verwundern, wie apodiktisch er behaupten kann, dass die ‚Seele‘ eine wesentliche Eigenschaft der Bedeutung (und damit des Objektes) ‚Mensch‘ sei.

DISKUSSION

15. Mit diesem Abschnitt über ‚wesentliche‘ und ’nicht wesentliche‘ gleich ‚akzidentiellen‘ / ‚kontingenten‘ / ‚arbiträren‘ Eigenschaften eines Bedeutungsobjektes O sind wir schon in den tiefsten Abgründen einer Ontologie bzw. einer Metaphysik gelandet.
16. Dazu muss man sich nochmals bewusst machen, dass die Ausdrücke E (die selbst sinnliche Muster der Wahrnehmung sind und die auch Abstraktionsprozessen unterliegen; man denke nur an die ‚type’/ ‚token‘ Unterscheidung der Linguisten) in Beziehung gesetzt werden zu Bedeutungselementen, die gegeben sind als aus der sinnlichen Wahrnehmung $latex K_{s}$ abstrahierte Objekte O, die in verschiedenen Abstraktionsstufen organisiert sind. Alle (!) diese Objekte setzen Wahrnehmungsprozesse voraus, die mit einer elementaren Form von Lernen verknüpft sind.
17. Wenn also ein Mensch A zu einem bestimmten Zeitpunkt t durch seine individuellen Lernprozesse in einer bestimmten Sprachgemeinschaft mit Sprache L ‚gelernt‘ hat, dass ein Ausdruck e sich mit bestimmten – aus der Wahrnehmung gewonnenen – Objekten O verbindet – als m(o,e) –, dann kann man folgende Unterscheidung treffen: (i) sofern sich diese Wahrnehmungsobjekte O auf Eigenschaften der umgebenden Welt W beziehen, die im Zeitraum des Lernens von Mensch A mehr oder weniger ‚konstant‘ / ‚unveränderlich‘ waren, dann ‚existiert‘ die ‚erlernte Bedeutung‘ O für den Menschen A und die gelernten Bestandteile von O sind für diesen Menschen A ‚wesentlich‘; ebenso für alle anderen Menschen, die mit diesem Aspekt der umgebenden Welt W in Berührung gekommen sind. Wenn (ii) die gelernten Eigenschaften O der umgebenden Welt aber ‚variabel‘ sind, mal so und mal so, also akzidentiell/ kontingent/ arbiträr, dann ‚kennt‘ der lernende Mensch A zwar diese möglichen Bedeutungen O‘, sie aber mit einem anderen Objekt O in Verbindung zu bringen, ist nicht notwendig, ist nicht zwingend, sondern muss sich aus der aktuellen kontingenten Situation ‚ergeben‘. Wenn üblicherweise ein Mensch nicht weiß ist (weil alle anderen in der Umgebung schwarz sind), dann wäre das Ereignis, dass ein Mensch auftritt, der weiß ist, ein ‚interessantes‘ Ereignis, das zu berichten lohnen würde.
18. Ein Mensch B mit einer anderen Sprache L‘ wird die Ausdrücke der Sprache L von Mensch A zunächst nicht verstehen (z.B. sei L= Arabisch und L’=Hebräisch). Wenn aber der Mensch A sich auf einen Aspekt X der umgebenden Welt W bezieht, den auch der Mensch B wahrnehmen kann, dann haben A und B die leise Chance, aufgrund der gemeinsamen Kenntnisnahme von X die hinreichend ‚gleichen Wahrnehmungen O(X)‘ zu haben, und dann kann B eventuell ‚begreifen‘, dass der arabische Ausdruck von A sich auf dieses gemeinsam wahrnehmbare O(X) bezieht, und er dann aufgrund seiner Kenntnis des L’=Hebräischen weiß, wie er den L= arabischen Ausdruck für O(X) im Hebräischen wiedergeben würde.
19. Wichtig ist hier, dass die ‚Existenz‘ einer Bedeutung O(X) generell von ‚existierenden Eigenschaften X in der umgebenden Welt W‘ abhängt UND (!!!) von den daran anknüpfenden Wahrnehmungsprozessen, die – stimuliert von X – zu den entsprechenden Bedeutungsobjekten O(X) führen. Existieren in diesem Sinne Bedeutungen O(X), dann kann man von ihren Eigenschaften sagen, dass sie ‚wesentlich‘ sind, wenn sie ’normalerweise immer‘ so vorkommen.
20. Solange man sich der sinnlichen Herkunft aller Bedeutungen bewusst ist, solange hat man auch keine Probleme damit, dass ‚Menschen‘ aufgrund ihrer genetischen Basis im Laufe der Zeiten zu ganz unterschiedlichen Erscheinungsweisen kommen können: verschiedene Hautfarben, verschiedene Körperformen, verschiedene Deformationen (keine Arme, verkrüppelte Beine, anders geformte Köpfe, …), unterschiedliche Intelligenzen, usw. Heute zusätzlich erweitert durch medizinische Operationen, Schönheitsoperationen, allerlei Prothesen und Implantate. Dass der Begriff ‚Mensch‘ vor diesem Hintergrund unterschiedliche Bedeutungen O aufgrund unterschiedlicher Gegebenheiten X in der Welt annehmen kann, sollte dann kein Problem sein.
21. Schwieriger wird es, wenn man – was in der Vergangenheit ständig geschah – glaubte, aus den empirisch gewonnenen Bedeutungen O(X) auf ‚allgemeine Strukturen‘ schließen zu können, die ‚hinter‘ den empirischen Eigenschaften in dem Sinne liegen, dass sie den empirischen Ereignissen ‚zeitlich und logisch vorausgehen‘. In diesen Zusammenhang gehört der populäre Geist-Materie-Dualismus, nach dem die materiellen Erscheinungen ‚Ausfluss‘ geistiger Strukturen sind, die als solche die ‚wesentlichen‘ Eigenschaften repräsentieren.
22. Psychologisch sind solche Denkfiguren verständlich, da sich die Antike auch die Frage gestellt hat, wie die vielfältigen empirischen Formen der umgebenden Welt trotz allem nicht ganz arbiträr sind, sondern offensichtlich gewissen ‚Regeln‘ / ‚Gesetzen‘ folgen. In Unkenntnis der modernen Physik und Biologie konnte man nur sehr allgemeine Annahmen machen, meist sehr statische. Heute beginnen wir zu verstehen, dass die Vielfalt der Formen auf spezifische Erzeugungsprozesse zurückgehen, die wiederum allgemeinen Gesetzen folgen. Diese Gesetze erlauben in der Umsetzung viel Variabilität, so dass Vielfalt und Regelhaftigkeit keinen Widerspruch darstellen.
23. Die Kernaussagen von Avicenna zu der Begriffslogik bis zu dieser Stelle kann man aber wohl aufrecht erhalten. Erst wenn man aufgrund von Erfahrungen anlässlich X Bedeutungen O(X) ausbilden konnte kann man mit diesen Bedeutungen Urteile der Art bilden ‚Etwas X existiert‘ oder ‚Ein Etwas X ist ein Etwas Y‘.
24. Wichtig ist hier aber, zu sehen, dass das ‚Denknotwendige‘ der Alltagslogik sich nicht aus den Ausdrücken E als solchen ergibt, sondern aus den Eigenschaften der mit den Ausdrücken verknüpften Bedeutungen O(X).
25. Bislang wurde hier nur angenommen, dass die Bedeutungsobjekte O ‚Hierarchien‘ bilden können. Dies erklärt, wieso eine Bedeutung ‚universell‘ sein kann im Sinne von Allgemeinbegriff – Instanzen. Im Fall von (Zid) (ist) (ein Mensch) wäre ‚Zid‘ eine Instanz von Mensch; oder im Fall von (Der Mensch) (ist) (ein Lebewesen) wäre (der Mensch) eine Instanz von (Lebewesen). Entsprechend wäre (Zid) (schläft) ein Urteil, in dem von Zid (als Instanz von Mensch) gesagt würde, er habe die Eigenschaft zu schlafen. Sofern man ’schlafen‘ als ‚typisch‘ für Menschen ansehen würde, wäre dies eine ‚wesentliche‘ Aussage, da es normalerweise so ist. Würde man sagen, der Mensch schläft nur gelegentlich, dann wäre es eine akzidentelle/ kontingente Eigenschaft, eben nicht wesentlich.
26. Diese Beispiele mit (ist)(weiß), (schläft), (sitzt) legen den Schluss nahe, dass die Bedeutung O(X) nicht nur ein gleichförmiges Etwas ist, sondern aus einer Menge von ‚unterscheidbaren Eigenschaften‘ [PROP] bestehen kann.
27. Daraus würde folgen, das z.B. die Instanz ‚Zid‘ und die Instanz ‚Hans‘ von der Bedeutung ‚Mensch‘ jeweils bestimmte Eigenschaften PROP_Hans und PROP_Zid aufweisen, die so sind, dass der Oberbegriff ‚Mensch‘ solche Eigenschaften PRP_Mensch aufweist, die sowohl Zid und Hans gemeinsamen haben; Zid und Hans können aber auch Eigenschaften aufweisen, die sie voneinander unterscheiden und die nicht in im universellen Begriff ‚Mensch‘ vorkommen.
28. Also $latex PROP_{Mensch} = PROP_{Zid} \cap PROP_{Hans}$ würde sowohl die Menge der gemeinsamen Eigenschaften der beiden Instanzen ‚Zid‘ und ‚Hans‘ bezeichnen als auch die Verbindung zwischen dem universellem Begriff und seinen Instanzen herstellen.
29. Stellt sich noch die Frage, was denn dann die ‚Eigenschaften‘ sind? Setzen wir den bisherigen Zusammenhang voraus, dann haben wir die Annahme einer umgebenden Welt W mit ‚Welteigenschaften‘ X und einen Menschen als ein System, das mittels seiner Sinnesorgane eine Wahrnehmung (‚perception‘) als Abbildung von bestimmten dieser Welteigenschaften X auf innere sensorische Muster $latex K_{s}$ realisieren kann ($latex perc: X \longrightarrow K_{s}$). Aus diesen Mustern $latex K_{s}$ lassen sich dann mittels Abstraktion unterschiedlichste Objekte O generieren ($latex \alpha: K_{s} \cup K_{p} \longrightarrow O$) (unterstellt, dass dabei implizite Denkprinzipien $latex K_{p}$ nach Avicenna mitwirken können (was nahezu alle Philosophen ähnlich angenommen haben)). Aus diesen Annahmen ergibt sich, dass jedwede Eigenschaft auch solch ein abstrahiertes Objekt aufgrund von Sinneseindrücken sein muss.
30. Fragt sich dann, ob sich Objekte und Eigenschaften von Objekten unterscheiden, und wie?
31. Intuitiv würde man sagen: Ja. Aber wie genau?
32. Hier könnte man Avicennas Begriffe ‚universell‘ und ‚wesentlich‘ bemühen: ein ‚echtes‘ Objekt umfasst andere Objekte (als Eigenschaften), die ihm ‚wesentlich‘ zukommen, d.h. ’normalerweise‘, ‚regelhaft‘; ein ‚unechtes‘ Objekt ist ein solches, das zwar als ‚Teil von einem echten Objekt‘ auftreten kann, normalerweise aber nicht alleine vorkommt. So wäre eine ‚Rose‘ tendenziell ein ‚echtes Objekt‘, da es mit bestimmten Eigenschaften ’normalerweise‘ auftritt, ‚Rot‘ wäre aber ein ‚unechtes‘ Objekt, da ‚Rot‘ normalerweise nicht isoliert auftritt sondern nur in Verbindung mit anderen Objekten; z.B. kann das Objekt ‚Rose‘ das Objekt ‚Rot‘ als Eigenschaft – also als unechtes Objekt – enthalten.
33. Die Unterscheidung von (echtem) Objekt und (unechtem) Objekt (als Eigenschaft) hängt damit von der ‚gelernten‘ Bedeutung ab: was tritt wann wie oft und welcher Konstellation auf.
34. ‚Wesentlich‘ wird hier interpretiert als ‚regelmäßige Erscheinung‘ (normal), und ’nicht wesentlich‘ bzw. kontingent bzw. akzidentell wird hier interpretiert als ’nicht regelmäßig‘, ’nicht normal‘, ‚gelegentlich‘, ‚zufällig‘ auftretend.

Fortsetzung folgt …

QUELLEN

  • Avicenna, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
  • Digital Averroes Research Environment
  • Stanford Encyclopedia of Philosophy, Aristotle’s Logic
  • Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7

Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER.

AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 3

Ausdruck, Ausdruck - einfacher, Ausdruck - sprachlicher, Ausdruck - zusammengesetzter, Avicenna, Bedeutung, Bedeutung - abstraktes Konstrukt, Bedeutung eines Wortes, Bedeutungsbeziehung, Bedeutungskorrelat, individuell, Logik, Logik - Antike, Objekt, universell

VORGESCHICHTE

1. In einem ersten Beitrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 1 hatte ich geschildert, wie ich zur Lektüre des Textes von Avicenna gekommen bin und wie der Text grob einzuordnen ist.
2. In einem zweiten Beitrag AVICENNAS ABHANDLUNG ZUR LOGIK – Teil 2 ging es um die Frage, warum überhaupt Logik? Avicenna führt erste Unterscheidungen zu verschiedenen Wissensformen ein, lässt aber alle Detailfragen noch weitgehend im Dunkeln.
In diesem Teil geht es jetzt um einfache und zusammengesetzte Begriffe.

AUSDRÜCKE: EINFACH UND ZUSAMMENGESETZT

3. In Weiterführung seiner Redeweise von sprachlich vermitteltem Wissen $latex K_{m}$ verstanden als ein Paar bestehend aus einem Bündel von sinnlichen Eindrücken $latex k \subseteq K_{s}$ einerseits und einem Ausdruck $latex e \in E, E \subseteq K_{s}$ andererseits, also m(k,e), führt er jetzt die Unterscheidung von ‚einfachen‘ und ‚zusammengesetzten‘ Ausdrücken ein. Der Ausdruck ‚einfach‘ bezieht sich dabei auf die Menge der ‚Bedeutungsbeziehungen‘, in denen ein Ausdruck e vorkommt. Kommt der Ausdruck e nur in einer Bedeutungsbeziehung vor, also m(k,e), dann ist er einfach. Kann man aber einen Ausdruck e zerlegen, so dass einzelnen Teilen $latex e_{i}$ jeweils eine eigene Bedeutungsbeziehung zugewiesen werden kann, dann ist er ‚zusammengesetzt‘, also etwa $latex e = \langle e_{1}, …, e_{n} \rangle$ mit $latex m_{1}(k_{1}, e_{1}), … m_{n}(k_{n}, e_{n})$.

EINFACHE AUSDRÜCKE: INDIVIDUELL ODER UNIVERSELL

4. Avicenna führt dann noch die weitere Unterscheidung ein, dass ‚einfache Ausdrücke‘ entweder ‚individuell‘ sein können oder ‚universell‘.

5. Er motiviert diese neuen Begriffe so, dass er sagt, dass ein einfacher Ausdruck e mit m(k,e) nur eine einzige Entität (‚entity‘) bezeichne, wohingegen ein einfacher Ausdruck m(k*,e), der als ‚universell‘ gilt, mit seiner Bedeutungskomponente ‚k*‘ viele Entitäten (‚many entities‘) bezeichne.

DISKUSSION

6. So einfach diese neuen Begriffe ‚einfach/ zusammengesetzt‘ sowie bei ‚einfach zusätzlich ‚individuell/ universell‘ klingen, so stehen sie für ein Geflecht von Problemen, das dies heute nicht als gelöst gelten kann.

7. Wie schon in der Diskussion von Teil 2 deutlich wurde, setzt die Diskussion der Unterscheidung der verschiedenen Wissensformen einen begrifflichen Rahmen voraus, der letztlich auf generelle Annahmen zum erkennen Subjekt hinausläuft, wie es etwa im Rahmen einer Erkenntnistheorie geleistet werden könnte, also ein abstraktes Modell eines erkennenden Subjektes, das den formalen Rahmen liefert, innerhalb dessen dann über spezielle Sachverhalte wie ’sprachliches‘ oder ‚logisches‘ Wissen gesprochen werden kann.

8. Schon die Einführung der Unterscheidung von sprachlichen Ausdrücken $latex E \subseteq K_{s}$, die in einer ‚Bedeutungsbeziehung‘ M zu anderen sinnlichen Ereignissen $latex K_{s} \subseteq K$ stehen, können als $latex M \subseteq K_{s} \times E$, wirft eigentlich zusätzliche Fragen auf, die bislang von Avicenna nicht geklärt wurden.

9. Nun zu sagen, dass ein einfacher Ausdruck e in genau einer Bedeutungsbeziehung m stehe, und die darin vorkommenden sinnlichen Ereignisse k genau ‚eine Entität‘ bezeichnen, legt die Vorstellung nahe, dass bestimmten Mustern sinnlicher Ereignisse k etwas ‚Abstrakteres‘ korrespondiert, nämlich ein ‚Objekt‘ o mit $latex o \in O$. Daraus würde folgen, dass die Bedeutungsbeziehung möglicherweise nicht direkt auf Muster k von sinnlichen Ereignissen abzielt, sondern auf abstrakte Objekte O, die aus den sinnlichen Mustern k durch einen Abstraktionsprozess $latex \alpha$ erzeugt werden; also $latex \alpha: KS \longrightarrow O$ und $latex M \subseteq O \times E$.

10. Nimmt man diese Interpretation an, dann ließe sich der Fall von ‚einfachen‘ Ausdrücken, die bedeutungsmäßig ‚universell‘ sind, so rekonstruieren, dass sich im Bereich der abstrakten Objekte O mehr als eine ‚Abstraktionsebene‘ denken lässt. Analog der Whitehead-Russelschen Typentheorie aus den Principia Mathematica gibt es dann Abstraktionsebenen von 1 bis n, und ein Objekt auf der Ebene j könnte alle Objekte von Abstraktionsebenen ‚kleiner als j‘ als ‚Instanzen‘ haben.

11. Dazu müsste man die Abstraktionsfunktion ein wenig verallgemeinern zu $latex \alpha: KS \cup O \longrightarrow O$, und man müsste sich noch die Hierarchie der Ebenen ‚dazudenken‘.

12. Beispiel: auf dem Tisch stehen verschiedene konkrete, einzelne Tassen $latex \{ t_{1}, …, t_{r} \}$; diese repräsentieren einzelne Entitäten (Ebene 1). Dazu gibt es den abstrakteren Begriff ‚Tasse‘ auf einer Ebenen 2. Auf dem Tisch befinden sich aber auch noch andere Gegenstände, z.B. ‚Teller‘, ‚Bestecke‘ usw. Die Begriffe ‚Teller‘ und ‚Besteck‘ bezeichnen Objekte der Ebene 2. Man könnte jetzt von diesen unterschiedlichen Objektarten weiter ‚abstrahieren‘ und z.B. den Begriff ‚Frühstücksgegenstände‘ auf Ebene 3 einführen. Die konkreten Tassen sind Instanzen des Begriffs ‚Tasse‘; die Begriffe ‚Tasse‘, ‚Teller‘, ‚Besteck‘ sind Instanzen von ‚Frühstücksgegenstände‘; es könnten aber auch natürlich die konkreten Tassen, konkreten Bestecke usw. als Instanzen des Begriffs ‚Frühstücksgegenstände‘ bezeichnet werden.

13. Dies würde bedeuten, dass man einem Ausdruck e zwar genau ‚eine Bedeutung‘ o zuordnen kann, diese Bedeutung o gehört aber zu einer Hierarchie von ‚Objekten‘ O, die, je nach Stellung in der Hierarchie der Bedeutungsobjekte, unterschiedliche andere Objekte von einer ’niedrigeren‘ Stufe/ Ebene‘ als ‚Instanzen‘ beinhalten kann. Dies führt dazu, dass man neben den bisherigen Unterscheidungen von Wissensformen noch eine weitere einführen müsste, nämlich das ‚Objektwissen‘ $latex K_{o}$, das eine Objekthierarchie umfasst, die aus dem sinnlichen Wissen $latex K_{s}$ mittels eines Abstraktionsprozesses $latex \alpha$ erzeugt wird.

Eine Fortsetzung findet sich HIER

QUELLEN

  • Avicenny, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
  • Digital Averroes Research Environment
  • Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
  • Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7

Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER.