(Letzte Änderungen: Mi 15.Okt.2014, 12:17h)
VORGESCHICHTE
Für einen Überblick zu allen vorausgehenden Beiträgen dieser rekonstruierenden Lektüre von Avicennas Beitrag zur Logik siehe AVICENNAS ABHANDLUNG ZUR LOGIK – BLITZÜBERSICHT.
1. Im letzten Beitrag entstand die Arbeitshypothese, dass aufgrund des ‚fließenden‘ Bedeutungsübergangs zwischen ‚echten‘ und ‚unechten‘ Objekten auf der Bedeutungsseite damit die Unterscheidung zwischen ‚Subjekt‘ (S) und ‚Prädikat‘ (P) auch fließend würde. Das würde die Unterscheidung ob die Terme ‚S‘ oder ‚P‘ sind aufheben. Anders ausgedrückt, die Terme in einer Schlussfigur erscheinen ‚invariant‘ bzgl. der Kategorisierung als ‚S‘ oder ‚P‘.
2. Verfolgt man den Gedanken der ‚Invarianz‘ weiter, dann sieht man sofort, dass die Anordnung der Prämissen 1 und 2 auch ‚invariant‘ ist gegenüber ‚Vertauschung‘. Hat man die Prämissen A1: (_ F M) und A2: (_M H) mit dem Muster, das die Schlussfigur 1 charakterisiert, dann erhält man durch Vertauschen der Reihenfolge A1: (_ M F) und A2: (_H M) die Schlussfigur 4 (die Avicenna nicht benutzt), und kann feststellen, dass diese Vertauschung nichts an der Bedeutungsstruktur und damit an der Folgerung ändert. Darüber hinaus sieht man, dass durch die Vertauschung der Prämissen auch die Quantoren der ersten und zweiten Prämisse gespiegelt wurden. Der ‚Wahrheitsgehalt‘ der Schlussfigur bleibt ‚erhalten‘.
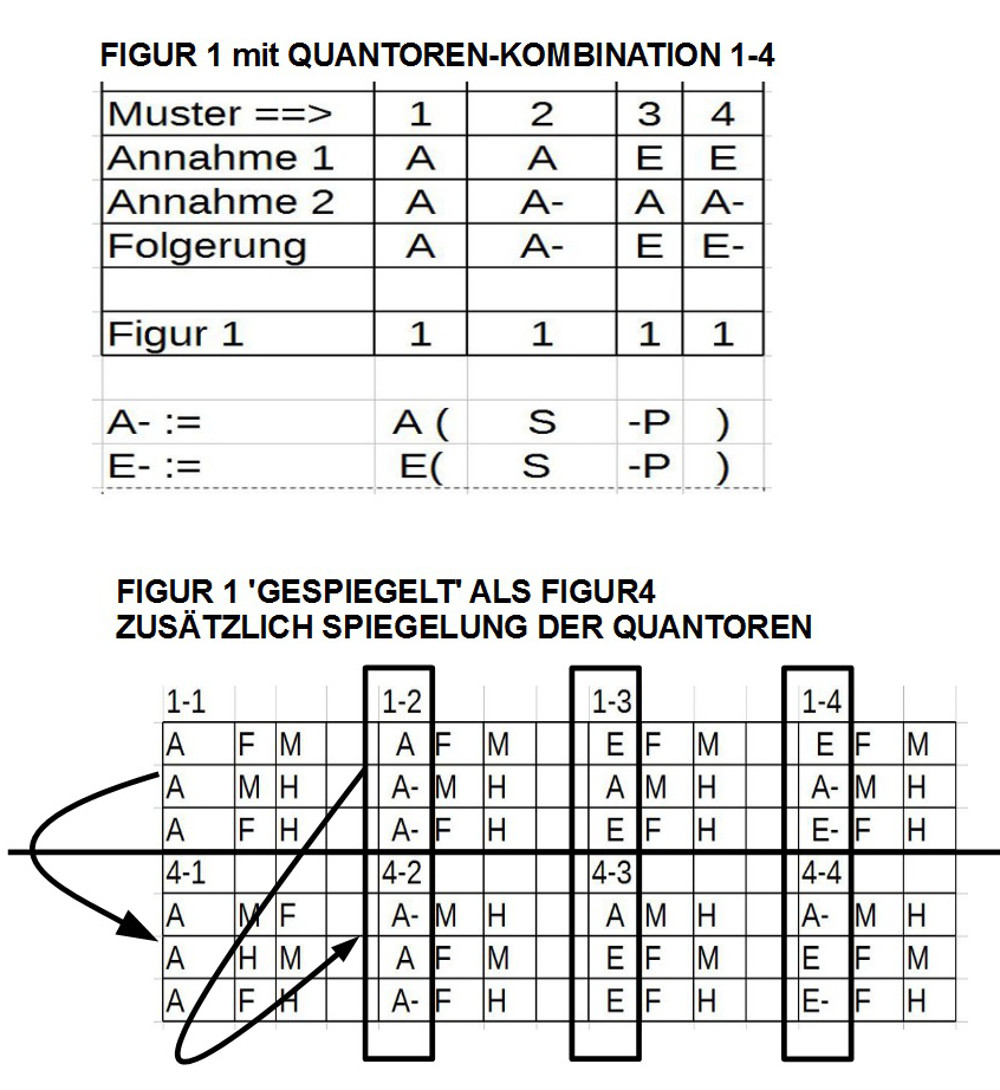
3. Es lieg nahe, den ‚Spiegelungstest‘ auch mit den Schlussfiguren 2 und 3 vorzunehmen. Hier die Ergebnisse:
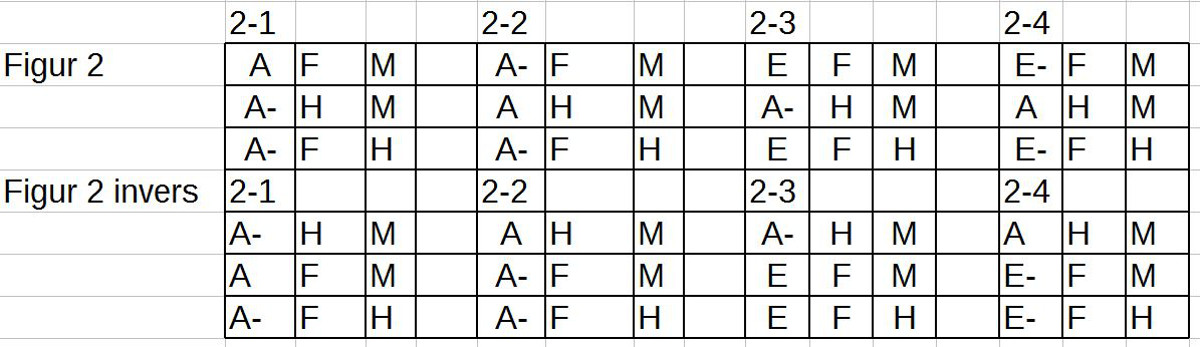
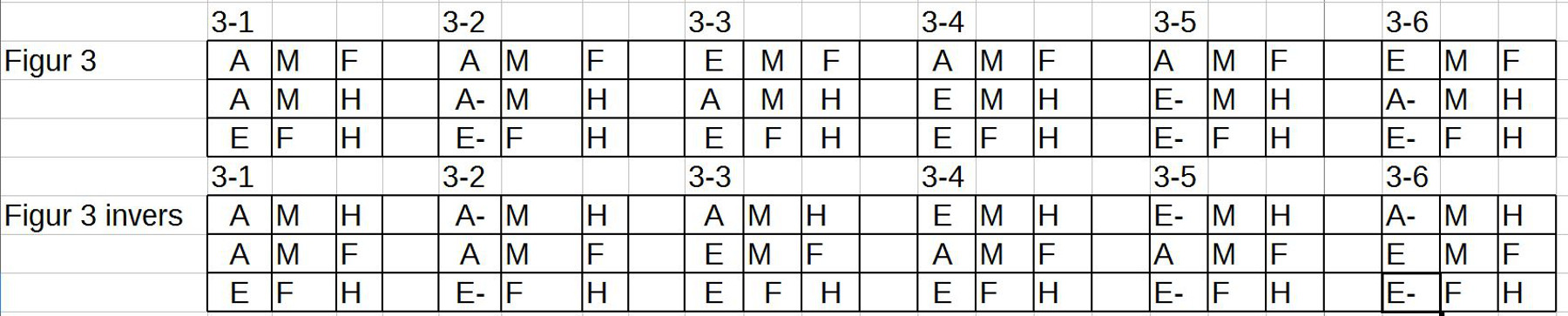
4. Man sieht, dass die Spiegelung in Form der Veränderung der ‚Abfolge‘ der Prämissen keine Wirkung auf den ‚Wahrheitsgehalt‘ besitzt. Dies wird verständlich, wenn man sich klar macht, dass die ‚Ausdrücke‘ E einer Sprache L ja nicht die ‚Bedeutung selbst‘ darstellen, sondern nur auf die Bedeutungsstrukturen ‚Bezug nehmen‘. Wie immer diese beschaffen sein mögen, die sprachlichen Strukturen ‚kodieren‘ diese nur. Und insoweit es sich bei den hier angesprochenen Sachverhalten um statische Beziehungsverhältnisse handelt, spielt die Abfolge der beschreibenden Äußerungen – zumindest in diesen Fällen — keine Rolle.
5. Fasst man alle Schlussfiguren (ohne ihre ‚bedeutungsgleichen‘ inversen Varianten) zusammen, dann erhält man folgende Tabelle:
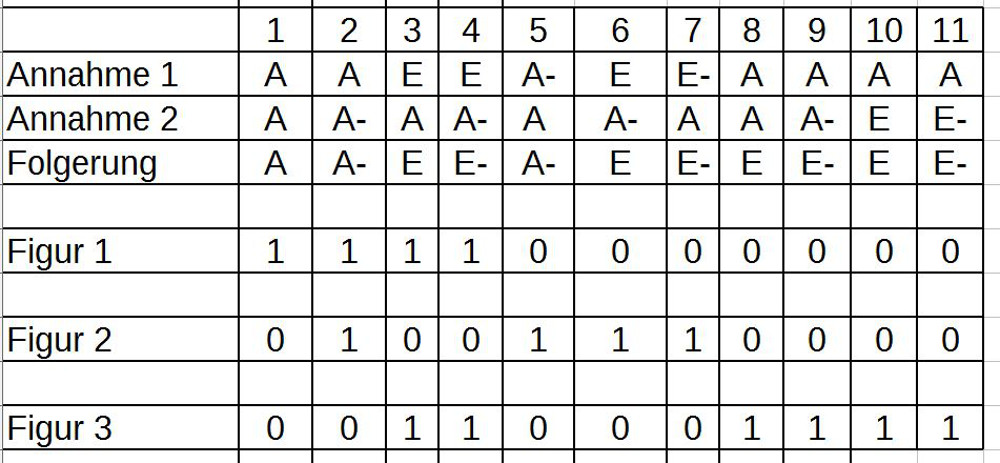
6. Angesichts dieser vielen ‚Invarianzen‘ drängt sich verstärkt die Frage auf, was denn dann der ‚harte Kern‘ an Strukturen ist, an denen sich der ‚Wahrheitsgehalt‘ einer Folgerung orientiert.
7. Bislang hat sich schon herausgeschält, dass es um ‚Beziehungen zwischen Mengen‘ geht (welche Elemente in welchen Mengen vorkommen), und um Eigenschaften, die diesen Elementen ‚zugesprochen‘ werden.
8. Die Schlussfiguren 1-3 (bzw. 1-4) setzen in den Prämissen genau drei verschiedene Mengen F, H und M voraus, zwischen denen jeweils F und H eine Beziehung zu M haben. Insofern ist M der ‚Mittelterm‘ (und F und H sind die ‚äußeren‘ Terme). Gefragt wird dann immer nach der sich daraus resultierenden Beziehung zwischen F und H. Die ‚Antwort‘ auf diese Frage wird als ‚Schlussfolgerung‘ präsentiert. Das folgende Bild zeigt die Verteilung der Quantoren für alle Schlusfiguren samt ihren Inversen.
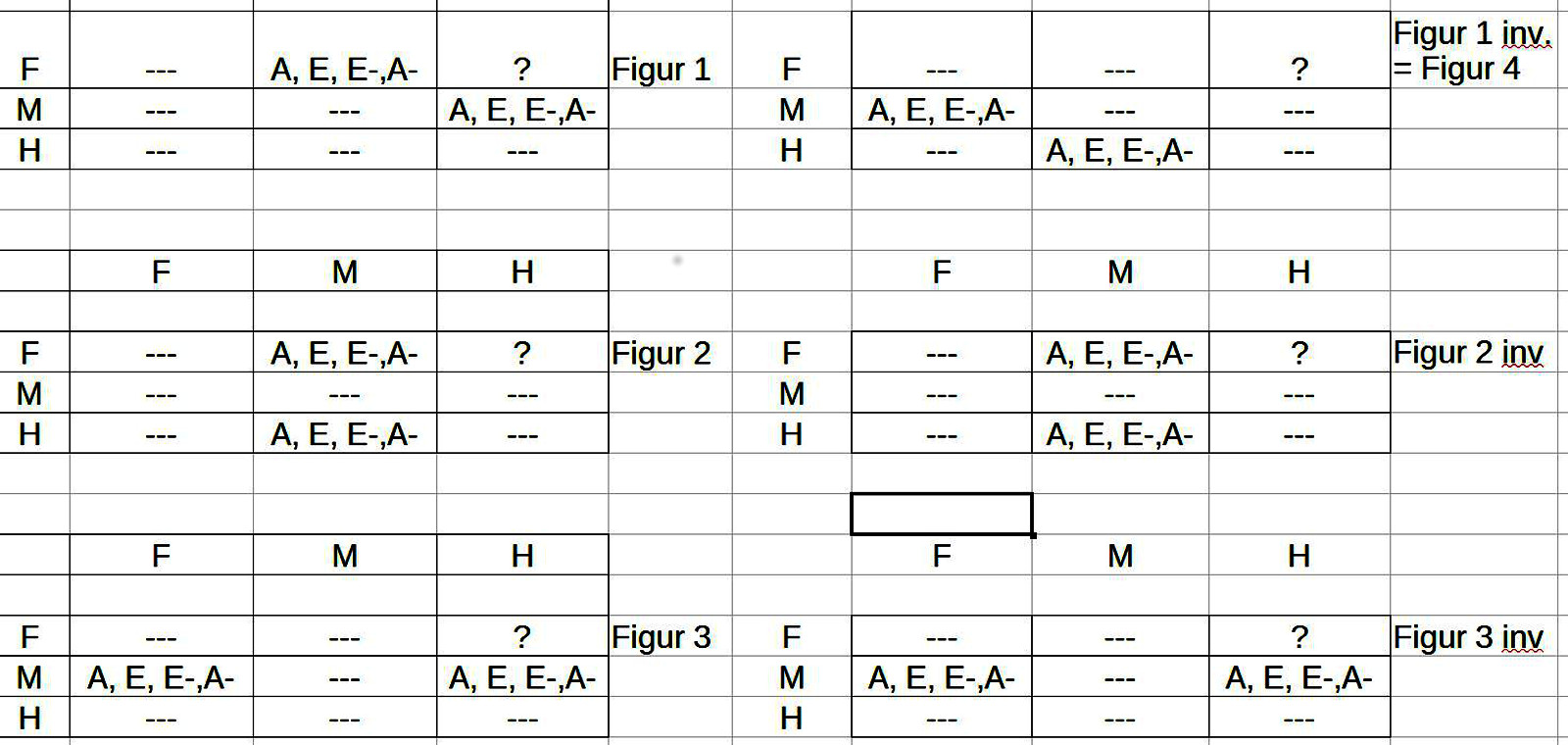
9. Man kann in dieser Darstellung schon sehen, dass es im Falle der Schlussfiguren 2 und 3 gar keine Spiegelung vergleichbar zu Figur 1 mit der Figur 4 gibt.
10. Betrachtet man nochmals Figur 1, dann kann man folgende Sachverhalte erkennen (siehe Bild): (i) Bei den Mengenverhältnissen gibt es eigentlich nur drei Fälle (A), (E) = (E-), sowie (A-). Zu jedem dieser drei Fälle für Prämisse 1 kann es dann wiederum kombinatorisch jeweils drei Fälle geben. Spielt man diese durch (das Bild zeigt dies nur für den Fall (A F M) in Prämisse 1), dann zeigt sich (ii) dass von den theoretisch möglichen Fällen 3 x 3 = 9 nur jeweils 3 x 2 = 6 geben kann. Dies ergibt sich daraus, dass eine Kombination von E und E bei dem Muster von Figur 1 zu keinem eindeutigen Schluss führt. Ein Partikularquantor E kann hier immer nur zusammen mit einem Allquantor A auftreten.
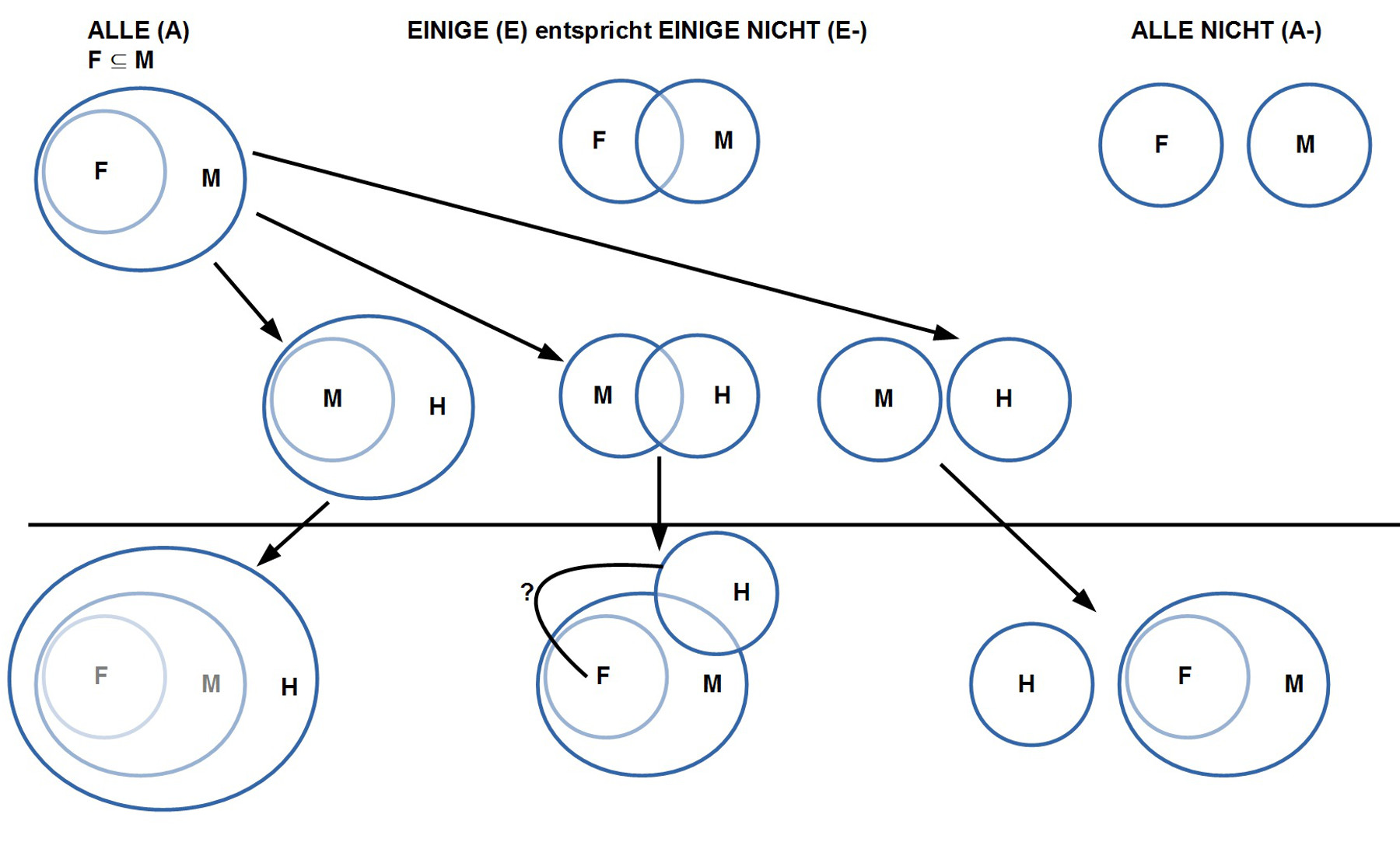
11. Es fragt sich, wieweit diese Überlegungen auch auf die anderen Schlussfiguren übertragbar sind. Im folgenden Bild sind nochmals alle formal möglichen Quantorenkombinationen für jede Schlussfigur aufgelistet mit der Legende: ‚1‘ := wird von Avicenna genannt, ‚?‘ := unbestimmt, ‚+‘ := würde einen Schluss zulassen:
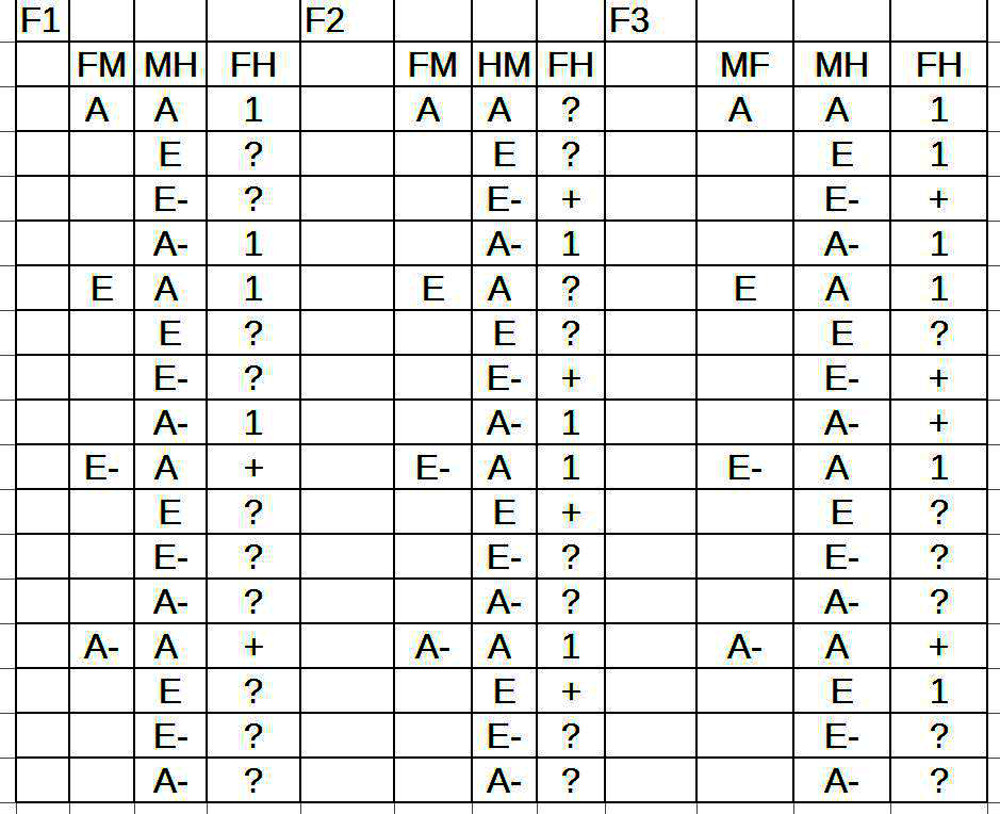
12. In der Tabelle kann man erkennen, dass es neben den Einsen ‚1‘, die anzeigen, dass diese Quantorenkombinationen in den drei ‚Schlussfiguren Verwendung finden, bei allen Schlussfiguren Fragezeichen ‚?‘ gibt, aber auch Pluszeichen ‚+‘. Dies würde bedeuten, dass es weitere mögliche Schlüsse gäbe, die aber von Avicenna nicht genannt werden.
13. Die Klassifikation ‚?‘ bzw. ‚+‘ habe ich spontan vorgenommen, ‚intuitiv‘. Es fragt sich, ob diese ‚intuitive‘ Zuordnung ‚richtig‘ ist, Eine Antwort auf diese Frage setzt voraus, dass man irgendwelche ‚Kriterien‘ explizit machen kann, anhand deren man die ‚intuitive‘ Klassifikation explizit ‚begründen‘ oder ‚widerlegen‘ kann. Dies soll hier versucht werden.
14. Aus der Geschichte der modernen Logik sind zahlreiche formale Kalküle bekannt, deren ‚Wahrheitsfähigkeit‘
nachgewiesen worden ist. Im vorliegenden Fall wird die Frage aber in einem spezifischen Kontext gestellt: (i) wir setzten hier – versuchsweise — eine allgemeine Bedeutungsfunktion auf der Basis einer dynamischen Objektstruktur voraus und (ii) im Kontext der dynamischen Objektstruktur stellt sich die Frage, wie es möglich ist, ‚zweifelsfrei‘ von zwei vorgegebenen Beziehungen in den Prämissen auf eine dritte Beziehung als Folgerung zu ’schließen‘.
15. Diese Frage hat mindestens zwei Aspekte: (i) einmal, ob und inwieweit wir ‚im Rahmen unseres Bewusstseins‘ Kriterien finden können, die solch eine Unterscheidung unterstützen und (ii) wie die ‚Maschinerie unseres Denkens‘, die dem bewussten Denken vorgelagert ist, diese Aufgabe lösen kann. Dabei fragen wir nicht ‚empirisch‘, ’nicht naturwissenschaftlich‘, sondern ‚logisch, ‚philosophisch‘ in dem Sinne, ob wir überhaupt eine rationale Konstruktion (ein formales Modell) finden können, das eine Erklärung liefern könnte. Dass es dazu dann möglicherweise noch eine empirische Struktur geben könnte, die die Aufgabe ‚anders‘ löst, wäre interessant, würde aber in diesem Kontext dann keine Veränderung bewirken.
16. Es wird notwendig sein, alle 3x 16 Fälle einzeln anzuschauen und zu überprüfen.
17. Darüber hinaus kann man die Frage stellen, ob man die Betrachtung auf andere ‚Typen von wahrheitsfähigen Sachverhalten‘ (auf andere Typen von analytisch wahren Sachverhalten) noch ausweiten kann. Denn die Beispiele mit den Syllogismen der Figuren 1-3(4) sind sehr eng. Und da wir von der modernen formalen Logik wissen, dass man mit den modernen Kalkülen beliebig komplexe Strukturen beschreiben kann, ist die Frage nach weiteren Sachverhalten eigentlich nur eine ‚rhetorische‘ Frage. Allerdings würden wir damit in Richtung einer allgemeinen Logiktheorie steuern. Möglicherweise ist dies hier noch zu früh.
Fortsetzung folgt
QUELLEN
- Avicenna, ‚Avicennas Treatise on Logic‘. Part One of ‚Danesh-Name Alai‘ (A Concise Philosophical Encyclopedia) and Autobiography, edited and translated by Farang Zabeeh, The Hague (Netherlands): Martinus Nijhoff, 1971. Diese Übersetzung basiert auf dem Buch ‚Treatise of Logic‘, veröffentlicht von der Gesellschaft für Nationale Monumente, Serie12, Teheran, 1952, herausgegeben von M.Moien. Diese Ausgabe wiederum geht zurück auf eine frühere Ausgabe, herausgegeben von Khurasani.
- Digital Averroes Research Environment
- Immanuel Kant, Critik der reinen Vernunft‘, Riga, 1781
- Konrad Lorenz, 1973, ‚Die Rückseite des Spiegels. Versuch einer Naturgeschichte des menschlichen Erkennens‘, München, Zürich: Piper
- Günther Patzig, ‚Die Aristotelische Syllogistik‘, 3. verb.Aufl., Göttingen: Vandenhoeck & Rupprecht, 1969
- Nicholas Rescher (1928 – ),The Development of Arabic Logic. University of Pittsburgh Press, 1964
- Hans-Jörg Sandkühler (Hg.) unter Mitwirkung von Dagmar Borchers, Arnim Regenbogen, Volker Schürmann und Pirmin Stekeler-Weithofer, ‚Enzyklopädie Philosophie‘, 3 Bd., Hamburg: FELIX MEINER VERLAG, 2010 (mit CD-ROM)
- Stanford Encyclopedia of Philosophy, Aristotle’s Logic
- Whitehead, Alfred North, and Bertrand Russell, Principia Mathematica, 3 vols, Cambridge University Press, 1910, 1912, and 1913; Second edition, 1925 (Vol. 1), 1927 (Vols 2, 3). Abridged as Principia Mathematica to *56, Cambridge University Press, 1962.
- Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume One. Merchant Books. ISBN 978-1-60386-182-3.
- Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Two. Merchant Books. ISBN 978-1-60386-183-0.
- Alfred North Whitehead; Bertrand Russell (February 2009). Principia Mathematica. Volume Three. Merchant Books. ISBN 978-1-60386-184-7
Eine Übersicht über alle bisherigen Blogeinträge nach Titeln findet sich HIER